Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание. Уравнения статики и динамики. Линеаризация.Содержание книги
Поиск на нашем сайте
Любой процесс или объект можно описать дифф или разностными уравнениями. Ур-е динамики описывает процессы в системе при произвольных вх воздействиях в течение времени. Ур-е статики описывает процессы в системе при постоянных вх воздействиях в установивш режиме. В основном системы описыв нелинейн дифф ур-ями, что затрудняет исследование системы и объекта. Замена нелинейного ур-я линейным нзв линеаризацией. Общий вид линейной системы автоматического управления
В реальных условиях большинство элементов автоматической системы являются не линейными.
5 Математическое описание. Преобразование Лапласа. Передаточная функция. Анализ и синтез САУ существенно упрощается при использовании прикладных математических методов операционного исчисления. Имеется функция вещественной переменной f(t), ей можно поставить в соответствие F(p), где f(t) – оригинал, F(p) – изображение.
Преобразование Лапласа обладает следующими свойствами: операциям дифференцирования и интегрирования в приведении вещественной переменной соответствуют эквивалентные алгебраические операции умножения и деления с использованием комплексной переменной. Применение преобразования Лапласа позволяет перейти от исходных дифференциальных уравнений к эквивалентным алгебраическим уравнениям в представительстве комплексной переменной. Передаточной функция звена или системы – отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.
Математическое описание. Частотные характеристики.(АФЧХ, ЛАХ и ЛФХ) Если на вход звена (системы) подать гармоническое воздействие
АФХ может быть получена из выражения передаточной функции W(p) заменой комплексной переменной р на мнимую переменную jw:
АФХ строится на комплексной плоскости в координатах вещественная составляющая по оси х; мнимая составляющая по оси у, при изменении частоты от 0 до ∞.
Математическое описание. Временные характеристики. Временная характеристика звена системы – закон изменения выходной величины в функции времени при изменении входной величины по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое. Зависит от характера звена. Ступенчатое воздействие при t=0,входная величина X
Линейное воздействие с постоянной скоростью
Переходная функция звена – реакция звена на единичное ступенчатое воздействие. Y(p)=W(p)*X(p); H(p)=>W(p)/p; L{1(t)}=1/p; h(t)=L-1[W(p)/p] Импульсная переходная или весовая функция – реакция звена на импульсное воздействие в виде δU Y(p)=W(p)*X(p); L[δ(t)]=1; K(p)=W(p)*1; k(t)=L-1[W(p)]; W(p)=pH(p)=k(p); k(t)=dh/dt Достоинством временных характеристик является то, что они могут быть получены экспериментально. Элементарные типовые звенья. Интегрирующее звено. Так называют звено с передаточной функцией W(s) = к/s. Его частотные и временные функции имеют следующий вид:
АФЧХ:
ЛАХ, ЛФХ:
Переходная характеристика:
k-коэфф усиления Элементарные типовые звенья. Апериодическое звено. Так называют звено с передаточной функцией W(s) = k/(Ts + 1). Его частотные и временные функции имеют следующий вид:
АФЧХ:
ЛАХ, ЛФХ:
Переходная характеристика:
Элементарные типовые звенья. Колебательное звено. Так называют звено с передаточной функцией:
АФЧХ:
ЛАХ,ЛФХ:
Переходная характеристика:
Элементарные типовые звенья. Дифференцирующее звено I-го порядка. Передаточная функция: W(p)=k(Tp+1) Элементарные типовые звенья. Дифференцирующее звено II-го порядка. Передаточная функция: W(p)=k(T2p2+2ETp+1)
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.56.150 (0.007 с.) |


 -интеграл Лапласа
-интеграл Лапласа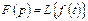

 – комплексная переменная;
– комплексная переменная;
 – передаточная функция.
– передаточная функция. , то после окончания переходных процессов на выходе устанавливаются колебания
, то после окончания переходных процессов на выходе устанавливаются колебания  той же частоты, но иной амплитуды и сдвинутые по фазе относительно входных колебаний.
той же частоты, но иной амплитуды и сдвинутые по фазе относительно входных колебаний. – амплитудно-фазовая характеристика есть отношение выходной величины к входной величине выраженной в комплексной форме.
– амплитудно-фазовая характеристика есть отношение выходной величины к входной величине выраженной в комплексной форме. – АЧХ
– АЧХ – функция частоты – ФЧХ
– функция частоты – ФЧХ