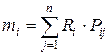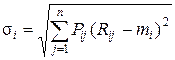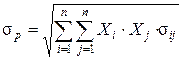Основные постулаты теории Марковица

На практике используют множество методик формирования оптимальной структуры портфеля ценных бумаг. Большинство из них основано на методике Марковица. Он впервые предложил ма­тематическую формализацию задачи нахождения оптимальной структуры портфеля ценных бумаг в 1951 г., за что позднее был удостоен Нобелевской премии по экономике.

Основная идея - статистически рассматривать будущий доход, приносимый финан­совым инструментом, как случайную переменную, т. е. доходы по отдельным инвестиционным объектам случайно изменяются в не­которых пределах.

Основные постулаты, на которых построена классическая портфельная теория Марковица:

- рынок состоит из конечного числа активов, доходности ко­торых для заданного периода считаются случайными величинами;

- инвестор в состоянии, исходя из статистических данных, получить оценку ожидаемых (средних) значений доходностей и их попарных ковариаций и степеней возможности диверси­фикации риска;

- инвестор может формировать любые допустимые (для дан­ной модели) портфели. Доходности портфелей являются также случайными величинами;

- сравнение выбираемых портфелей основывается только на двух критериях: средней доходности и риске;

- инвестор не склонен к риску, в том смысле, что из 2 портфелей с одинаковой доходностью он обязательно предпочтет портфель с меньшим риском.

Показатели оценки дохода и риска в модели Марковица

По модели Марковица определяются показатели, характеризующие объем инвестиций и риск что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.

В качестве ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.

Математическое ожидание дохода по i -й ценной бумаге (m_i) рассчитывается следующим образом:

Где:

R_i – возможный доход по i -й ценной бумаге;

P_ij – вероятность получения дохода;

n – количество ценных бумаг.

Для измерения риска служат показатели рассеивания, поэтому, чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Мерой рассеивания является среднеквадратическое отклонение:

В отличие от вероятностной модели, параметрическая модель допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды. Эти статистические данные представляют собой ряды доходностей за последовательные периоды в прошлом.

Любой портфель ценных бумаг характеризуется двумя величинами:

· ожидаемой доходностью

Где:

m_p – ожидаемая доходность портфеля, %

X_i – доля общего вложения, приходящаяся на i -ю ценную бумагу;

m_i – ожидаемая доходность i -й ценной бумаги, %;

 

· мерой риска – среднеквадратическим отклонением доходности от ожидаемого значения

Где:

s _p – мера риска портфеля;

X_i и X_j – доли общего вложения, приходящиеся на i -ю и j -ю ценные бумаги;

s _ij – ковариация между доходностями i -й и j -й ценных бумаг;

n – число ценных бумаг портфеля.

Модель Шарпа

В 1960-х годах Уильям Шарп первым провел регрессионный анализ рынка акций США. Во избежание высокой трудоемкости Шарп предложил индексную модель. Причем он не разработал нового метода составления портфеля, а упростил проблему таким образом, что приближенное решение может быть найдено со значительно меньшими усилиями. Шарп ввел b-фактор, который играет особую роль в современной теории портфеля.

Где: s _iM – ковариация между темпами роста курса ценной бумаги и темпами роста рынка;

s² _M – дисперсия доходности рынка.

Показатель «бета» характеризует степень риска бумаги и показывает, во сколько раз изменение цены бумаги превышает изменение рынка в целом.

Если β>1 то данную бумагу можно отнести к инструментам с повышенной степенью риска, т.к. ее цена движется в среднем быстрее рынка. Если β<1, то степень риска этой бумаги относительно низкая, поскольку в течение периода глубины расчета ее цена изменялась медленнее, чем рынок. Если β<0 то в среднем движение этой бумаги было противоположно движению рынка в течение периода глубины расчета.

В индексной модели Шарпа используется тесная корреляция между изменением курсов отдельных акций. Предполагается, что необходимые входные данные можно приблизительно определить при помощи всего лишь одного базисного фактора и отношений, связывающих его с изменением курсов отдельных акций. Как правило, за такой фактор берется значение какого-либо индекса. Зависимость доходности ценной бумаги от индекса описывается формулой:

Где: r_i – доходность ценной бумаги i за данный период;

r_I – доходность на рыночный индекс I за этот же период;

a _iI – коэффициент смещения;

b _iI – коэффициент наклона;

e _iI – случайная погрешность.

Оптимальный портфель

Оптимальный портфель - эффективный портфель, которому инвестор отдает предпочтение, поскольку параметры риска/воз­награждения этого портфеля приближены к функции полезности инвестора.

Цель оптимального портфеля - обеспечить оптимальное соче­тание выгодности, надежности и ликвидности ценных бумаг, фи­нансовых вложений для инвестора.

На практике используют множество методик формирования оптимальной структуры портфеля ценных бумаг. Большинство из них основано на методике Марковица.