
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие жидкость – пар. Закон РауляСодержание книги Поиск на нашем сайте
Пусть в состоянии равновесия находятся жидкость и выделяющийся из нее пар. В соответствии с теоремой равновесия Гиббса химический потенциал любого компонента в системе одинаков во всех фазах:
Выразим химический потенциал i -го компонента в жидкой фазе через его термодинамическую активность, а в паровой фазе – через его парциальное давление, то есть примем, что паровая фаза идеальна. Тогда получим:
Преобразуем уравнение:
Значение выражения, заключенного в скобки, найдем из граничного условия: если xi = 1, то γi = 1,
где Подставим в уравнение вместо выражения в скобках его значение:
Выразив активность через мольную долю и коэффициент активности, получим:
Уравнение (2.8) выражает основной закон жидких растворов – закон Рауля. Применительно к идеальным жидким растворам (γi → 1) уравнение (2.8) запишется
Рассмотрим идеальный жидкий раствор, состоящий из летучих компонентов А и В, тогда:
Выразим мольную долю компонента А через мольную долю компонента В: хА = 1 – хВ. Общее давление над раствором складывается из парциальных давлений компонентов р = рА + рВ, тогда
Таким образом, зависимость давления насыщенного пара компонентов и общего давления пара от состава раствора является линейной. Зависимость давления насыщенного пара от состава двухкомпонентного раствора представляется в виде диаграммы р(рА, рВ) – х (рис. 2.2).
Для реального раствора, содержащего летучие компоненты А и В общее давление над раствором равно:
Отклонения давления пара от линейной зависимости в сторону больших значений называют положительными, а в сторону меньших значений – отрицательными. Величина и вид отклонений зависят от сил взаимодействия между частицами. Силы взаимодействия межу частицами идеального раствора такие же, как и в чистых жидкостях, поэтому отклонений не возникает. В реальных растворах при уменьшении сил межмолекулярного взаимодействия усиливается испарение. Следовательно, увеличивается давление насыщенного пара и возникает положительное отклонение от линейной зависимости. Закономерности для растворов с отрицательными отклонениями имеют противоположный характер (рис. 2.3).
а б Рис. 2.3. Диаграмма состояния реальных растворов: а – с отрицательными отклонениями; б – с положительными отклонениями Состав равновесного с жидким раствором пара (уi) определяется согласно закону Дальтона:
Для представления данных по фазовому равновесию жидкость-пар кроме рассмотренных диаграмм применяются также диаграммы давление пара – состав (р – х(у)), температура кипения – состав (Т – х(у)) и состав пара – состав раствора (y – x) (рис. 2.4).
Рис. 2.4. Диаграммы давление пара – состав (р – х(у)), температура кипения – состав (Т – х(у)) и состав пара – состав раствора (y – x) На представленных диаграммах: точке А соответствует чистому компоненту А (100 %); точке В – чистому компоненту В (100 %); На диаграмме р – х(у): 1 – кривая зависимости давления насыщенного пара от состава пара; 2 – кривая зависимости давления насыщенного пара от состава жидкости. Область ниже кривой состава пара отвечает состоянию гомогенной системы – пара; область выше кривой состава жидкости отвечает состоянию жидкости. На диаграмме Т – х(у): 1 – кривая зависимости температуры кипения от состава пара; 2 – кривая зависимости температуры кипения от состава жидкости. Область выше кривой состава пара отвечает состоянию гомогенной системы – пара; область ниже кривой состава жидкости отвечает состоянию жидкости. Область, лежащая между кривыми состава пара и состава жидкости отвечает состоянию гетерогенной системы жидкость-пар, любая точка внутри этой области характеризует состояние равновесия между жидкостью и паром. Например, на диаграмме Т – х(у) в точке О при температуре Т 0 находится гетерогенная система, состоящая из жидкости и пара общий состав которой равен х 0. Точки с и d выражают составы равновесных жидкости х В и пара у В.
Таким образом, составы жидкости и равновесного с нею пара в общем случае неодинаковы. Если известна масса гетерогенной смеси в точке О m, то по правилу рычага можно рассчитать массы равновесных фаз:
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.210 (0.008 с.) |

 .
.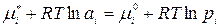 .
. .
.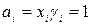 и
и  ,следовательно,
,следовательно, ,
, – давление насыщенного пара над индивидуальным i- м компонентом при температуре раствора.
– давление насыщенного пара над индивидуальным i- м компонентом при температуре раствора. ,
, .
. , (2.8)
, (2.8) .
.

 Для описания зависимости давления насыщенного пара компонента от состава реального раствора используют закон Рауля в виде:
Для описания зависимости давления насыщенного пара компонента от состава реального раствора используют закон Рауля в виде: .
.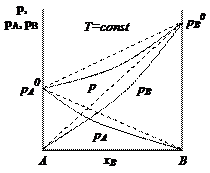

 – для идеального раствора;
– для идеального раствора; – для реального раствора.
– для реального раствора.
 .
.


