
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Химический потенциал индивидуального идеального газа.Содержание книги
Поиск на нашем сайте
Химический потенциал
Свободная энергия системы (энергия Гиббса G и энергия Гельмгольца F) зависит от внешних условий:
Эта зависимость является полной для простейших систем, состоящих из одного компонента. Термодинамическая система может состоять как из одного, так и из нескольких компонентов. Очевидно, что величина свободной энергии многокомпонентной системы будет зависеть как от внешних условий (Т, р, или V), так и от природы и количества веществ, составляющих систему, т. е. свободная энергия, как и любая термодинамическая функция, является экстенсивным свойством системы.В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы. Рассмотрим термодинамическую систему, состоящую из k компонентов. Пусть n1, n2, …, nk – число моль 1-го, 2-го, …, k -го компонентов. Тогда свободная энергия Гиббса является функцией следующих переменных: G = f(p, T, n1, n2, …, nk) Продифференцируем по всем переменным:
Введем обозначение:
………………….
где μ1, μ2, …, μk – химические потенциалы 1-го, 2-го, …, k -го компонентов соответственно. В общем виде
Аналогичное выражение получаем для свободной энергии Гельмгольца: F = f(V, T, n1, n2, …, nk)
Таким образом, химический потенциал – это частная производная от свободной энергии по количеству моль i -го компонента при постоянстве соответствующих внешних параметрах и числе моль всех остальных компонентов. Таким образом, химический потенциал является парциальной мольной энергией Гиббса (при р, Т = const):
Свободная энергия – это общее свойство системы, химический потенциал характеризует свойства отдельного компонента, входящего в систему. Химический потенциал является интенсивным свойством системы, т.к. не зависит от массы системы. При р, Т = const уравнение (2.1) имеет вид:
В этом случае изменение энергии Гиббса, то есть полезная работа системы, обусловлена только изменением состава системы в результате протекания химической реакции или вследствие обмена веществом между системой и окружающей средой. Уравнение (2.2) выражает взаимосвязь между общим свойством системы и свойствами каждого ее компонента. Приняв, что химический потенциал является постоянной величиной, проинтегрируем уравнение (2.2):
Константа интегрирования равна нулю, поскольку, если все ni = 0, энергия Гиббса также равна нулю. Для индивидуального вещества
т.е. химический потенциал индивидуального вещества равен мольной энергии Гиббса. При равновесии dG = 0 и уравнение (2.1) принимает вид:
Полученное уравнение является общим условием равновесия в системе с переменным составом при р, Т = const. Химический потенциал индивидуального идеального газа. Рассмотрим термодинамическую систему, представляющую собой идеальный газ. Химический потенциал идеального газа равен:
где Так как
то где Если процесс протекает при Т = const, частную производную можно заменить полной. Тогда
Уравнение состояния 1 моль идеального газа:
тогда
Проинтегрируем в интервале от р0 до р:
где μ 0, р 0 – химический потенциал и давление идеального газа в стандартном состоянии. За стандартное состояние принято состояние идеального газа при р 0= 1 атм. Тогда
Стандартный химический потенциал – это химический потенциал при давлении газа 1 атм. Химический потенциал в стандартном состоянии μ 0 зависит только от температуры и не зависит от давления, т.е. μ 0 = f(T). Из уравнения (2.3) видно, что под знаком логарифма стоит безразмерная величина, равная отношению давления р к стандартному давлению р 0 = 1 атм. Поскольку μ =
где Правило фаз Гиббса
Пусть при р, Т = const в состоянии равновесия существует система, состоящая из k компонентов и m фаз. На систему оказывают влияние s внешних параметров (на практике обычно s = 2 – это р и Т). Поставим задачу рассчитать число термодинамических степеней свободы данной системы. Число термодинамических степеней свободы – это число независимых параметров состояния данной системы, оно равно общему числу параметров состояния системы за вычетом числа уравнений, связывающих эти параметры. Для определения состава любой фазы, содержащей k компонентов достаточно указать содержание (k – 1) компонентов. Так как концентрации компонентов обычно выражены в массовых или мольных долях и концентрация одного из компонентов будет определена, если известны концентрации остальных компонентов. Например, двухкомпонентная система представляет собой 20 %-й водный раствор уксусной кислоты. Тогда массовую долю второго компонента – воды можно рассчитать: 100 – 20 = 80 %. Поэтому указывать, сколько в системе содержится воды необязательно. Если в системе m фаз, то для описания их состава требуется m(k–1) переменных. Кроме того, на систему влияют внешние параметры, количество которых равно s. Следовательно, общее количество переменных,влияющих на состояние системы равно: m(k – 1) + s. Однако не все эти переменные независимы друг от друга, та как при равновесии распределение каждого из компонентов между различными фазами должно удовлетворять теореме равновесия Гиббса:
Очевидно, что таких уравнений для каждого из компонентов будет на единицу меньше числа фаз. Например, если m = 3, то для первого компонента запишется только два уравнения:
тогда число уравнений, связывающих химические потенциалы одного компонента равно m – 1, а всех k компонентов – k(m – 1). Для определения числа термодинамических степеней свободы вычтем из общего числа параметров, описывающих состояние данной системы число уравнений, связывающих их:
После преобразований получим:
Уравнение (2.5) выражает основной закон фазового равновесия – правило фаз Гиббса. Если на систему влияют два внешних параметра (р и Т), то правило фаз Гиббса записывается
Из двух и более компонентов
С чистым растворителем Рассмотрим разбавленный раствор нелетучего вещества. Для такого раствора коэффициент активности i -го компонента γi → 1 и ai → xi. Зависимость давления пара i -го компонента над раствором от его мольной доли выражается уравнением Рауля:
Пусть 1 – летучий растворитель, а 2 – нелетучее растворенное вещество. Общее давление пара над раствором равно
Давление пара над чистым нелетучим веществом р 2 ≈ 0, следовательно им можно пренебречь, тогда
Так как мольная доля x < 1, то давление пара над раствором нелетучего вещества ниже по сравнению с давлением пара над чистым растворителем при той же температуре (рис. 2.5).
тогда получим
Преобразуем
вещества по сравнению с давлением пара чистого растворителя при той же температуре равно мольной доле растворенного вещества. На рисунке: 1 – кривая зависимости давления насыщенного пара над чистым твердым растворителем (кривая возгонки) 2 – кривая зависимости давления насыщенного пара над чистым жидким растворителем (кривая испарения); 3 – кривая зависимости давления насыщенного пара над раствором нелетучего вещества с мольной долей х2; р10 – давление насыщенного пара над чистым растворителем при температуре Т1; р1 – давление насыщенного пара над раствором при температуре Т1. Из рисунка видно, что р1 < р10. Химический потенциал
Свободная энергия системы (энергия Гиббса G и энергия Гельмгольца F) зависит от внешних условий:
Эта зависимость является полной для простейших систем, состоящих из одного компонента. Термодинамическая система может состоять как из одного, так и из нескольких компонентов. Очевидно, что величина свободной энергии многокомпонентной системы будет зависеть как от внешних условий (Т, р, или V), так и от природы и количества веществ, составляющих систему, т. е. свободная энергия, как и любая термодинамическая функция, является экстенсивным свойством системы.В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы. Рассмотрим термодинамическую систему, состоящую из k компонентов. Пусть n1, n2, …, nk – число моль 1-го, 2-го, …, k -го компонентов. Тогда свободная энергия Гиббса является функцией следующих переменных: G = f(p, T, n1, n2, …, nk) Продифференцируем по всем переменным:
Введем обозначение:
………………….
где μ1, μ2, …, μk – химические потенциалы 1-го, 2-го, …, k -го компонентов соответственно. В общем виде
Аналогичное выражение получаем для свободной энергии Гельмгольца: F = f(V, T, n1, n2, …, nk)
Таким образом, химический потенциал – это частная производная от свободной энергии по количеству моль i -го компонента при постоянстве соответствующих внешних параметрах и числе моль всех остальных компонентов. Таким образом, химический потенциал является парциальной мольной энергией Гиббса (при р, Т = const):
Свободная энергия – это общее свойство системы, химический потенциал характеризует свойства отдельного компонента, входящего в систему. Химический потенциал является интенсивным свойством системы, т.к. не зависит от массы системы. При р, Т = const уравнение (2.1) имеет вид:
В этом случае изменение энергии Гиббса, то есть полезная работа системы, обусловлена только изменением состава системы в результате протекания химической реакции или вследствие обмена веществом между системой и окружающей средой. Уравнение (2.2) выражает взаимосвязь между общим свойством системы и свойствами каждого ее компонента. Приняв, что химический потенциал является постоянной величиной, проинтегрируем уравнение (2.2):
Константа интегрирования равна нулю, поскольку, если все ni = 0, энергия Гиббса также равна нулю. Для индивидуального вещества
т.е. химический потенциал индивидуального вещества равен мольной энергии Гиббса. При равновесии dG = 0 и уравнение (2.1) принимает вид:
Полученное уравнение является общим условием равновесия в системе с переменным составом при р, Т = const. Химический потенциал индивидуального идеального газа. Рассмотрим термодинамическую систему, представляющую собой идеальный газ. Химический потенциал идеального газа равен:
где Так как
то где Если процесс протекает при Т = const, частную производную можно заменить полной. Тогда
Уравнение состояния 1 моль идеального газа:
тогда
Проинтегрируем в интервале от р0 до р:
где μ 0, р 0 – химический потенциал и давление идеального газа в стандартном состоянии. За стандартное состояние принято состояние идеального газа при р 0= 1 атм. Тогда
Стандартный химический потенциал – это химический потенциал при давлении газа 1 атм. Химический потенциал в стандартном состоянии μ 0 зависит только от температуры и не зависит от давления, т.е. μ 0 = f(T). Из уравнения (2.3) видно, что под знаком логарифма стоит безразмерная величина, равная отношению давления р к стандартному давлению р 0 = 1 атм. Поскольку μ =
где
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.247 (0.007 с.) |


 (2.1)
(2.1)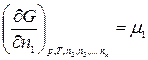

 ,
, .
. .
. .
. ;
; . (2.2)
. (2.2) .
. ,
,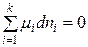 . (2.3)
. (2.3) ,
, – мольная энергия Гиббса (изобарный потенциал 1 моль идеального газа).
– мольная энергия Гиббса (изобарный потенциал 1 моль идеального газа). ,
,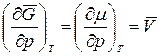 ,
, – мольный объем идеального газа (объем 1 моль газа).
– мольный объем идеального газа (объем 1 моль газа).
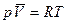 ;
; ,
,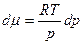


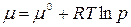 . (2.3)
. (2.3)
 – стандартная мольная энергия Гиббса.
– стандартная мольная энергия Гиббса.
 ,
,
 . (2.5)
. (2.5) .
. .
. .
.
 Выразим мольную долю растворителя х1 через мольную долю растворенного вещества х2:
Выразим мольную долю растворителя х1 через мольную долю растворенного вещества х2: ,
,
 . (2.9)
. (2.9)


