В ходе лекции рассматриваются различные способы организации деятельности с Интернет-ресурсами в процессе преподавания геометрии

Среди ЦОРов особое место занимают Интернет-ресурсы. Интернет-среда становится важнейшим в современном обществе источником информации, в том числе, образовательной. Учителя математики не могут не учитывать этого в своей повседневной педагогической практике. Освоение Интернет-технологий в самое ближайшее время станет одной из базовых компетенций учителя. Интернет-ресурсы, во-первых, должны стать значимым источником новой информации и предоставлять эксклюзивный материал для моделирования уроков; во-вторых, стать источником и организатором самообразования учителя; в-третьих, способствовать профессиональной рефлексии собственного и чужого опыта, в-четвертых, позволяет развить у учащихся основные компетентности, необходимые ему на современном этапе развития общества (фундаментальность общеобразовательной подготовки; способность учиться; коммуникабельность, умение работать в коллективе; способность самостоятельно мыслить и действовать; способность решать нетрадиционные задачи, используя приобретенные предметные, интеллектуальные и общие знания, умения и навыки).
Интернет-ресурсы на уроке (структура ресурсов)

1. Использование образовательных ресурсов, созданных на базе университетов, компьютерных фирм с целью изучения определенных тем, курсов (например, учителя биологии, химии, физики, астрономии могут обращаться на занятиях к образовательным ресурсам, которые на современном научном уровне представляют интегрированные знания: данные космических обсерваторий, спутников, анимация физических, химических процессов, динамических компьютерных моделей и мн.др.).

2. Интернет-ресурсы электронных библиотек, различных энциклопедий, текстов, а также самые различные ресурсы, созданные энтузиастами, (например, при использовании групповой формы работы, охватывается большой по объему материал, идет оценивание, анализ, выделение главного, защита своей точки зрения перед одноклассниками).

 

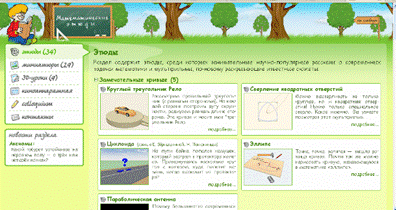
Несколько Интернет-ресурсов, которые будут интересны учителям при подготовке уроков геометрии, при организации проектной деятельности школьников, так как содержат интересный интерактивный, иллюстративный и информационный материал.

http://www.etudes.ru/ru/mov/. Сайт «Математические этюды».
На сайте представлены этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях.

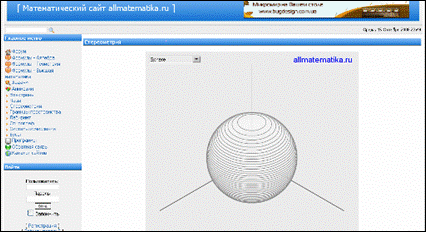
http://allmatematika.ru/page.php?18 «Математический сайт allmatematika.ru»
На сайте представлены интересные модели стереометрии, для которых можно менять размеры, тип фигуры. Модели будут интересны для исследования учащимися при организации кружковых и факультативных занятий.

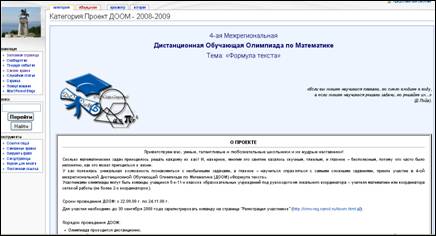
Это только пример такого рода Интернет-ресурсов, которые можно использовать на уроках геометрии.

3. Интернет-ресурсы (ЦОРы - цифровые образовательные ресурсы), созданные по результатам проведенных телекоммуникационных проектов (например, используются сайты, сделанные педагогами и их учащимися – по краеведению, окружающей природе, архитектуре города, знаменитым людям, по результатам их исследований, поисков, творческих работ в проектной деятельности)

Примером такого рода Интернет-ресурсов может служить сайт Дистанционной Обучающей Олимпиады по математике (ДООМ), которая уже 4 год проводится на страницах ТолВики. В олимпиаде участвуют не только команды учащихся России, но и стран Ближнего Зарубежья. Методической ценностью данного ресурса является богатейший материал, собранный на его страницах участниками проекта (учителями и учениками). Вот уже четвертый год олимпиада объявляет новую тему и ребята, участвующие хотя бы раз в ДООМ, ждут с нетерпением нала нового этапа проекта.
http://itc.tgl.ru/wiki/index.php/Категория:Проект_ДООМ_-_2008-2009

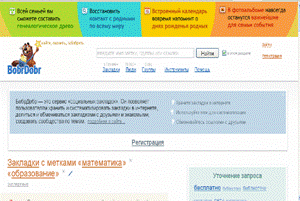
Однако появились образовательные ресурсы, выстраивающие целенаправленный диалог с пользователем, предполагающие его активность. Имеются в виду ресурсы, материалы которых требуют от учителя активности в перестройке предоставляемой ими информации с целью переноса этой информации из виртуального пространства Интернета в реальное познавательное пространство урока. А также организацию деятельности учащихся в данном виртуальном пространстве.

Характер использования Интернет-ресурсов при изучении геометрии определяется составом материалов, размещенных на различных сайтах. Некоторые из них могут быть использованы непосредственно в учебное время: на уроках и факультативных занятиях; некоторые же предоставляют материал для самостоятельной работы учащихся при выполнении домашних заданий и разного рода исследовательских работ.

Как источником хранения учебных материалов можно пользоваться сервисами для хранения закладок. Например, учитель предлагает ребятам на уроке (по группам) создать коллекцию закладок по теме «Векторы в пространстве». При этом ребята не только самостоятельно ведут поиск Интернет-ресурсов, но и пользуются всем массивом закладок, которые разместили пользователи данного сервиса. Задания подобного рода создают благоприятную среду для вовлечения учащихся в поисковую и исследовательскую деятельность при обучении геометрии, а также позволяют вырабатывать у них способность и даже, наверное, привычку к классификации и систематизации всей информации, таким образом, формируя у ребят способность учиться.

Сервис для хранения закладок (http://bobrdobr.ru) Закладки с метками «математика» и «образование»

ВикиВики – сетевой ресурс, который дае возможность при представлении материала проследить взаимосвязи с помощью гипертекста. На этот ресурс педагогам можно обратить пристальное внимание, как на площадку для проведения проектов, создание простейших математических энциклопедий, созданных руками ребят, а также использование уже готовых материалов многочисленных энциклопедий, организованных в среде ВикиВики.

Эта среда играют важную роль в развитии коммуникативных навыков у ребят, так как взаимодействие между людьми устанавливается через взаимодействие между статьями. С помощью ВикиВики возможно организовать проведение тренинга, семинара, интерактивной лекции, дистанционного курса. В этом случае ведущий тренинга заранее размещает тексты заданий и ссылки на дополнительный материалы. Обучающиеся выполняют задания, читают тексты, фиксируют свою деятельность. Ведущий занятие полностью контролирует деятельность учащихся (это одна из стандартных функций среды ВикиВики), имеет возможность исправить ошибки, оставить комментарии, которые немедленно будут видны обучающимся.

Вики- среда, как энциклопедия	ВикиВики как среда для организации проектной деятельности школьников

Большое разнообразие социальных сервисов позволяет каждому учителю выбирать и использовать их с учетом особенностей участников проекта. Предлагаем вам познакомиться с предложенными социальными сервисами и составить собственное мнение о каждом из них.

Интернет — наиболее динамично развивающаяся сегодня информационная среда. Характер, целеполагание и качество профессиональных Интернет-ресурсов весьма различны, как и состав представленных в них материалов. Поэтому педагогическая наука, с одной стороны, находиться в постоянном поиске способов адаптации новых мультимедиа технологий к уже имеющимся в арсенале учителя методикам, а с другой, осуществляет поиск новых оригинальных способов вовлечения компьютерных технологий в урок.

Проектируя учебное занятие, важно, чтобы каждый преподаватель помнил простую мысль: компьютер в учебном процессе – не механический педагог, не заместитель или аналог преподавателя, а средство при обучении детей, усиливающее и расширяющее возможности его обучающей деятельности.

Важность линии геометрических величин определяется следующими моментами.

1) В реальной действительности мы постоянно сталкиваемся с необходимостью измерения и оценки расстояний, площадей и объёмов фигур. (Примеры подобрать самостоятельно).

2) На основе материала данной темы осуществляется знакомство школьников с важными идеями, понятиями и методами метрической геометрии, расширяются возможности применения аналитического метода.

3) Реализуются внутрипредметные и межпредметные связи на основе взаимодействия аксиоматического метода, теории действительного числа, инфинитезимальных методов (бесконечно малых), метода координат и т. д.

4) Совершенствуются вычислительные навыки, навыки тождественных преобразований и решения уравнений и неравенств.

5) На данном материале, как правило, реализуется метод опорного элемента при решении задач

В школьном курсе математики изучаются следующие скалярные величины: длина отрезка, мера угла, площади многоугольника и круга, объёмы многогранников и тел вращения, длина окружности, площадь поверхности тел вращения.

Изучение скалярных геометрических величин в школе осуществляется концентрически: 1 концентр – 1 – 6 классы - пропедевтический, 2 концентр – 7-11 классы – основной.

1этап. В курсе 1-4 классов у школьников развивается наглядно-интуитивное представление о величинах и их практическом измерении. Здесь они знакомятся с различными единицами измерения длины и площади, основными соотношениями между ними; измеряют и сравнивают длин отрезков и площади фигур, составленных из единичных отрезков и квадратов, с помощью линейки и палетки вычисляют периметр многоугольника, а также площадь прямоугольника (по формуле). Уже здесь учащиеся начинают производить действия с именованными числами: + и – величин, * и: величин на число, а также сравнение величин.

2 этап. В 5-6 классе представления о геометрических величинах систематизируются и углубляются. В частности, если в начальной школе отрезок и его длина воспринимаются как один и тот же объект, то в 5-ом классе учащиеся получают возможность установить различие между фигурой и её величиной, записываемой в виде числа с наименованием.

Это достигается на основе сопоставления результатов выполнения двух основных задач: построения отрезка заданной длины и измерения длин данного отрезка. Если в первом случае ответ неоднозначен, то во втором результат однозначен.

При изучении площадей и объёмов реализуется тот же план, что и при изучении длин отрезков: а) определение площади и объёма не даётся, а лишь поясняется, что для величин различных поверхностей и вместимостей сосудов надо знать площадь или объём соответствующих фигур; б) на конкретных примерах вводятся свойства площадей и объёмов, единицы их измерения, обращается внимание на то, что в отличие от длины и мер углов равенство площадей или объёмов фигур вовсе не означает равенство этих фигур; в) вводятся и наглядно обосновываются формулы для площади прямоугольника и объёма прямоугольного параллелепипеда. Решаются соответствующие текстовые задачи.

В 6 классе обоснование вводятся важные в практическом отношении формула для длин окружности и площади круга.

3 Основной этап изучения геометрических величин 7-11 классов.

На этом этапе происходит переход от вычислительно-прикладного аспекта к формально-логическому.

В учебнике А.В. Погорелова в §1 в явном виде вводятся аксиомы откладывания и измерения отрезков и углов. Вопрос об измерении отрезков и углов. Вопрос об измерении отрезков и углов в практическом плане не ставится.

В учебнике Л.С. Атанасяна изложение связано с практическими измерениями. Описывается процесс измерения, на наглядном уровне поясняются свойства длины отрезков и градусных мер углов, описываются приборы для измерения расстояний и углов на местности. В аксиоматике (в Приложении 1) есть только аксиомы измерения и откладывания отрезка (аксиом измерения углов нет).

Понятие о площадях и объёмах в учебнике А.В. Погорелова вводится также аксиоматически. Площадь простой фигуры (объём простого тела) – это положительная величина, численное значение которой обладает свойствами: 1)-3).

В учебнике Л.С. Атанасяна и др. площадь определяется как величина части плоскости, занимаемой многоугольником, измерения площадей и объектов с помощью единичных квадратов и кубов и обосновываются основные свойства площадей и объёмов.

В основу изучения площадей плоских фигур и объёмов многогранников в школьных курсах геометрии кладутся формулы S прямоугольника (S квадрата) и V прямоугольного параллелепипеда. (Можно и S треугольника и V тетраэдра и другие).

Можно выделить следующие четыре подхода к изучению площадей:

1. Сравнение площадей (подход Адамара)

В основе подхода - теорема о том, что площади (или объёмы) 2-х прямоугольников (прямоугольных параллелепипедов), имеющих равные основания, относятся между собой как их высоты.

Данный способ обладает достаточной общностью и вместе с тем не согласуется с известными с 5-6 классов способом измерения и имеет чересчур формальный для школы характер. Этот переход использован в учебнике А.В.Погорелова.

2. Традиционный подход (учебники Килелёва, Фетисова 1957 г., Атанасяна). После рассмотрения основных допущений о площадях вводится понятие об измерении площади прямоугольника при помощи сетки квадратов последовательно для случаев, когда обе стороны выражаются через единичный отрезок как:

1.) натуральное число;

2.) конечная десятичная дробь (рациональное число);

3.) бесконечная десятичная дробь (иррациональное число).

3. В 3-ем наиболее сложном случае площадь определяется либо как предел последовательности площадей прямоугольников, длины сторон которого выражаются рациональными числами, либо через введение двух последовательностей приближённых рациональных значений площади по недостатку и по избытку.

4. (на основе равносоставленности) – учебник Глагольева, 1954 г.

В явном виде рассматривается понятие равносоставленности. Определяются условия, при которых параллелограммы и прямоугольники равносоставлены. Рассматривается вывод формулы площади прямоугольника (прямоугольного параллелепипеда) для натуральных и рациональных измерений, а для иррациональных измерений формулы даются без доказательства. Данный подход также громоздок и не обладает достаточной психологической убедительностью в силу последнего допущения.

Наиболее оптимальным в настоящее время учителя считают классический подход (2-й подход) без рассмотрения третьего случая, либо принятие формулы площади квадрата за аксиому.

После доказательства (вывода) формулы площади прямоугольника, пользуясь элементарными методами (теоремой Бойяи-Гервина – 12 равновеликих многоугольника равносоставлены) выводят формулы для площадей остальных прямоугольников, либо разбивая, либо дополняя новый многоугольник.

В основе изложения теории объёмов многогранников лежит формула для объёма прямоугольного параллелепипеда, доказываемая совершенно аналогично формуле для площади прямоугольника.

В силу равносоставленности равновеликих призм вывод формул для объёмов наклонных параллелепипедов и призм можно осуществить элементарными методами. Соответствующие соображения иллюстрируются на наглядных моделях, а выводы аналогичны тем, которые применялись в планиметрии.

Основная методическая проблема при выводе формул для объёмов многогранников является соответствующая формула для тетраэдра (теорема Дена). По этой теореме для вывода этой формулы необходимо использовать неэлементарные методы, связанные с операцией интегрирования (явно или неявно). Подход, при этом используемый, как правило, отражается и на методике изложения теории объёмов тел вращения.

1 подход – метод исчерпывания («чёртова лестница») (учебники Киселёва, Погорелова) осуществляется в двух вариантах:

Рассматривая линию геометрических величин в школе можно предложить ряд тем для подготовки докладов учащимися, например:

1. Вычисление длины окружности и число π в историческом контексте.

2. Вычисление объёмов тел с помощью интегралов.

3. Различные подходы к вычислению объёмов многогранников и круглых тел.

Контрольные вопросы

1. Перечислите основные скалярные геометрические величины, изучаемые в школьном курсе.Что такое величина? Какими свойствами обладает любая скалярная величина?

2. В чём суть аксиоматического введения скалярных геометрических величин и конструктивного? И какой путь является основным в школьном курсе?

3. Какую роль играет понятие равносоставленности в теории площадей и объектов?

4. Каковы основные цели изучения линии геометрических величин в школьном курсе?

5. Что известно учащимся о геометрических величинах из пропедевтического курса математики?

6. Каковы методические подходы к изучению длин отрезков в школьном курсе?

7. Какие 4 основных подхода можно выделить при изучении площадей в школьном курсе геометрии? Суть каждого из этих подходов?

8. Какие подходы используются в основной школе при изучении длины окружности и площади круга?

9. В чём суть метода исчерпывания при построении теории объёмов многогранников?

10. Интегральный подход к нахождению объёмов геометрических тел.

11. Нахождение объёмов с помощью принципа Кавальери и формулы Симпсона.

12. Каковы возможные подходы к построению теории площадей поверхностей тел вращения в школьном курсе?