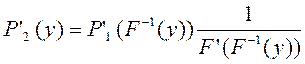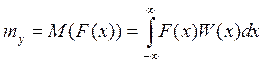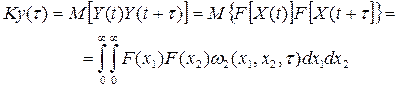Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Континуальной управляющей средойСодержание книги
Поиск на нашем сайте
Если теперь записать выражение для сигнала управления в оригиналах, то получим:
где S – некоторая область пространственно-временного континуума. Если ввести функцию xj0(r,t), равную xj(r,t) в пределах области В и равную нулю вне этой области, то полученное в оригиналах выражение можно распространить на все пространство, включая область S:
Используемая матрица Aij(k,w ), для управляющей континуальной среды, должна быть подчинена определенным требованиям, аналогичным требованиям физической реализуемости в одномерном случае. При этом класс функций Aij(k,w ) естественно определяется свойствами среды и доступности ее физической реализуемости при синтезе, а это связано с технологическими возможностями и ограничениями, накладываемыми применяемыми материалами. Решение задач синтеза континуальных преобразующих сред с заданными операторами преобразования сигналов может осуществляться на основе искусственных сред, обладающих дискретно-аналоговой или, иначе, квазиконтинуальной структурой. Поэтому особое значение приобретает создание управляющих моделирующих установок, в полной степени отвечающих условиям континуальности и реализуемости. Видимо, это особый тип устройств, который не может быть реализован на основе использования только методов математического моделирования и их реализации на дискретных (цифровых) ЭВМ. Такие моделирующие установки наиболее близки по принципам своей работы к физическим системам преобразования информации и позволяют определить искомые функции распределения параметров сред в пространстве и определению законов их изменения в пространстве и во времени под воздействием внешних воздействий. Значительный интерес представляет использование пространственно-временных управляемых структур для моделирования вероятностных систем. Они могут формировать сигнал с заданными характеристиками (функция распределения, корреляционные функции и т.д.) Математические методы, разработанные для этих преобразований, основываются на предположении безынерционности нелинейного преобразователя [10, 11, 13]. При таком анализе преобразователь описывается уравнением:
Y = F(X) (2.7) где Х – входной сигнал, характеризующий случайный процесс во времени; Y - выходной сигнал, который является случайным процессом, свойства которого в каждый момент времени определяется значением входного сигнала X и видом нелинейного преобразования – F. В случае однозначной монотонной зависимости выходной функции Y от Х, можно обратную зависимость записать в виде:
Х = F-1(Y).
При этом если Р1(х) – функция распределения случайной величины, W1(х) –соответственно плотность распределения этой величины, то необходимо найти Р2(y) и W2(y) выходной случайной величины, при наличии зависимости (2.7). Тогда распределение Y будет иметь вид:
P2(y) = W(Y < y) = W(F(х) < y)= W (X < F-1(y)) = P1(F-1(Y)). Таким образом:
Отсюда можно получить выражение для плотности вероятности:
Для определения другого значения можно воспользоваться выражением:
Более сложно решается вопрос о вычислении автокорреляционной функции Фурье и ее изображения:
где x1,x2 – случайные величины, w 2(x1,x2 ,t ) – вторая функция плотности вероятности. Таким образом, для вычисления автокорреляционной функции на выходе нелинейного элемента необходимо знать вторую функцию плотности вероятности. В частном случае можно вычислить для нормального (Гауссова) процесса значение w2 при известной автокорреляционной функции. Приведенные классические методы с некоторыми дополнениями могут быть использованы для проектирования вероятностных преобразователей и определения их характеристик.
1. Основные направления в архитектуре процессоров. Конвейер команд. Конвейер команд Идея конвейера команд была предложена в 1956 году академиком С. А. Лебедевым. Как известно, цикл команды представляет собой последовательность этапов. Возложив реализацию каждого из них на самостоятельное устройство и последовательно соединив такие устройства, мы получим классическую схему конвейера команд. Для иллюстрации воспользуемся примером. Выделим в цикле команды шесть этапов: 1. Выборка команды (ВК). Чтение очередной команды из памяти и занесение ее в регистр команды. 2. Декодирование команды (ДК). Определение кода операции и способов адресации операндов. 3. Вычисление адресов операндов (ВА). Вычисление исполнительных адресов каждого из операндов в соответствии с указанным в команде способом их адресации. 4. Выборка операндов (ВО). Извлечение операндов из памяти. Эта операция не нужна для операндов, находящихся в регистрах. 5. Исполнение команды (ИК). Исполнение указанной операции. 6. Запись результата (ЗР). Занесение результата в память.
Рис. 52. Логика работы конвейера команд
На рис. 52 показан конвейер с шестью ступенями, соответствующими шести этапам цикла команды. В диаграмме предполагается, что каждая команда обязательно проходит все шесть ступеней, хотя этот случай не совсем типичен. Так, команда загрузки регистра не требует этапа ЗР. Кроме- того, здесь принято, что все |тапы могут выполняться одновременно. Без конвейеризации выполнение девяти Команд заняло бы 9 х 6 = 54 единицы времени. Использование конвейера позволяет сократить время обработки до 14 единиц. Конфликты в конвейере команд Полученное в примере число 14 характеризует лишь потенциальную производительность конвейера команд. На практике в силу возникающих в конвейере конфликтных ситуаций достичь такой производительности не удается. Конфликтные ситуации в конвейере принято обозначать термином риск (hazard), а обусловлены они могут быть тремя причинами: · попыткой нескольких команд одновременно обратиться к одному и тому же ресурсу ВМ (структурный риск); · взаимосвязью команд по данным (риск по данным); · неоднозначностью при выборке следующей команды в случае команд перехода (риск по управлению).
2. Построение однородно структурированных, континуальных вычислительных и управляющих сред. Нейронные вычислительные системы.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.217.176 (0.007 с.) |

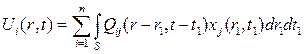 ,
,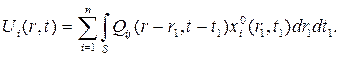
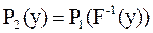 (2.8)
(2.8)