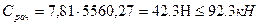Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение сил, действующих на тихоходный валСодержание книги
Поиск на нашем сайте
Силы, возникающие в зацеплении – окружная, радиальная и осевая, определены ранее в п.5.1.4. Дополнительная неуравновешенная радиальная сила от муфты:
где DМ – диаметр центров пальцев муфты, мм.
Определение реакций в опорах и построение эпюр изгибающих и крутящих моментов
Рассмотрим реакции в опорах от действия сил Ft и Fm в горизонтальной плоскости. При этом считаем, что шестерня расположена относительно опор симметрично, а = b = ℓo/2, а сила Fm направлена в сторону увеличения прогиба вала (худший случай). Сумма моментов относительно опоры А:
Сумма моментов относительно опоры В:
Проверка: 0,00=0
Рис. 5.4. Схема нагружения тихоходного вала.
Определяем реакции в опорах от действия сил Fr и Fa в вертикальной плоскости. Для этого составляем сумму моментов всех сил относительно опор А и В и находим опорные реакции.
Проверка: 0,00=0
Определяем суммарные изгибающие моменты в предполагаемых опасных сечениях I-I под колесом и в сечении II-II рядом с подшипником, ослабленных галтелью: В сечении I-I:
В сечении II-II:
В сечении I-I:
В сечении II-II:
Эквивалентные моменты в указанных сечениях:
В сечении I-I:
В сечении II-II:
Определяем диаметры валов в этих сечениях, мм:
Допускаемые напряжения на изгиб для валов и вращающихся осей принимаем [sизг] =50¸60 МПа. В сечении I-I:
В сечении II-II:
Расчет тихоходного вала на сопротивление усталости
В опасном сечении I–I определяем запасы усталостной прочности и сравниваем их с допускаемыми. Определяем запас усталостной прочности по изгибу
и кручению
где s-1 = (0,4–0,5) sв – предел контактной выносливости при изгибе, МПа; t-1 = (0,2–0,3) sв – предел контактной выносливости при кручении, МПа; sа и tа – амплитуда цикла при изгибе и кручении. При симметричном цикле и работе вала без реверса sа = suзг; sm =0. tm = tа = 0,5 tкр, МПа. suзг – напряжение изгиба в рассматриваемом сечении, МПа; tкр – напряжение кручения в рассматриваемом сечении, МПа.
Ws (нетто) – момент сопротивления сечения вала при изгибе; Wt (нетто) – момент сопротивления сечения вала при кручении. Для опасного сечения вала со шпоночной канавкой
где dк – диаметр вала под колесом, м; Кs – эффективный коэффициент концентраций напряжений при изгибе; Кt – эффективный коэффициент концентраций напряжений при кручении (табл. 5.5); Кd – коэффициент влияния абсолютных размеров поперечного сечения вала (табл. 5.6); Кv – коэффициент влияния поверхностного упрочнения (табл. 5.7.); ys и yt – коэффициенты чувствительности к асимметрии цикла напряжений (табл. 5.8.). Обобщенный коэффициент запаса усталостной прочности в опасных сечениях определяют по уравнению Гофа и Полларда
где [S] = 1,2–2,5 – допускаемый коэффициент запаса усталостной прочности. В сечении I-I: σзг=153,5168*103/0,1*603=7,40 МПа τ=107,74*103/0,2*603=6,21МПа σ-1=0,45*σв=0,45*760=342 MПа τ-1=0,25*σв=0,25*760=190 Mпа Kσ=1,7 Kd=0,81 Kf=1 Kτ=1,7 ψτ=0,05 ψσ=0 Sσ= Sτ= S= то запас прочности сбережен В сечении II-II: σзг=161,52*103/0,1*503=12,88691МПа τ=107,74*103/0,2*503=11,5837МПа Kσ=1,75 Kd=0,81 Kf=1 Kτ=1,55 ψτ=0,05 ψσ=0 Sσ= Sτ= S=
то запас прочности сбережен. Подбор и расчет подшипников Быстроходный вал
После назначения диаметра посадочных мест вала для установки подшипников качения выбирают для опор тип подшипника и схему их установки. При выборе типа подшипника в первую очередь принимают во внимание значение и направление нагрузки, действующей на опору, размеры посадочных мест вала и корпуса, способ смазывания, удобство монтажа и его стоимость. Если Fa > 0,25Fr (6.1) Fa =3916Н выбираем радиально-упорные шарикоподшипники. №46308, a=26, D=90мм, B=23мм, С=50,8, С0=26. Компоновку этих подшипников на валах цилиндрических передач производим по схеме “враспор”, т.е. стремимся к минимальному расстоянию между реакциями в опорах lo¢: lo¢ = lo + В – 2с (6.2) где В – ширина подшипника, мм; с – смещение точки приложения радиальной реакции относительно торца подшипника, мм
где d – внутренний диаметр подшипника, мм; D – наружный диаметр подшипника, мм. С= 27,4мм lo¢ = 121,2мм Для определения реакций в опорах направление силы Fm принимаем таким, чтобы оно совпадало с направлением силы Ft (худший случай), и составляем уравнения суммы моментов относительно опор А и В в горизонтальной плоскости.
Проверка: 0,00= 0;
Реакции в опорах от сил Fa и Fr, действующих в вертикальной плоскости, определяли по уравнениям п. 5.1.4. Суммарная радиальная нагрузка, действующая на подшипник в опоре А:
Суммарная радиальная нагрузка, действующая на подшипник в опоре В:
В радиально-упорных шарикоподшипниках при действии на них радиальных нагрузок возникают осевые составляющие реакций S, Н
По отношению
Определяем эквивалентную динамическую нагрузку в опорах А и В, Н;
где V – коэффициент вращения, V = 1; при вращении внутреннего кольца подшипника; FrА, FrВ – радиальная нагрузка в опоре, Н; FаА, FаВ – расчетная осевая нагрузка в опоре, Н; КБ - коэффициент безопасности; КБ = 1,3 для редукторов; КТ – температурный коэффициент; КТ = 1 (при температуре до 1000С); X, Y – коэффициенты осевой и радиальной нагрузок выбираем по таблице 6.1. По таблице 6.2. по Lh и n находим отношение
Тогда
где Р – значение эквивалентной динамической нагрузки в более нагруженной опоре, Н.
Условия подбора подшипника выполняются. Тихоходный вал
Так как частота вращения на тихоходном валу n2 значительно меньше частоты вращения на быстроходном валу n1 выбираем радиальные шарикоподшипники (табл.5.9). Выписываем характеристики подшипника №310, D=110, B=27, С=61,8 С0=36. Для определения реакций в опорах направление силы Fм принимаем таким, чтобы оно совпадало с направлением силы Ft (худший случай), и составляем уравнения суммы моментов относительно опор А и В в горизонтальной плоскости. Суммарная радиальная нагрузка, действующая на подшипник в опоре А:
Суммарная радиальная нагрузка, действующая на подшипник в опоре В:
Определяем эквивалентную динамическую нагрузку в опорах А и В, Н;
где V – коэффициент вращения, V = 1; при вращении внутреннего кольца подшипника; FrА, FrВ – радиальная нагрузка в опоре, Н; FаА, FаВ – расчетная осевая нагрузка в опоре, Н; КБ - коэффициент безопасности; КБ = 1,3 для редукторов; КТ – температурный коэффициент; КТ = 1 (при температуре до 1000С); X, Y – коэффициенты осевой и радиальной нагрузок выбираем по таблице 6.1.
По таблице 6.2. по Lh и n находим отношение где Р – значение эквивалентной динамической нагрузки в более нагруженной опоре, Н.
Условия подбора подшипника выполняются.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.55 (0.01 с.) |

 , (5.2.9)
, (5.2.9)
 (5.2.10)
(5.2.10)


 (5.2.11)
(5.2.11)
 ;
; 

 (5.2.12)
(5.2.12)
 (5.2.13)
(5.2.13)

 ;
; 
 , Нмм (5.2.14)
, Нмм (5.2.14) , Нмм (5.2.15)
, Нмм (5.2.15)

 , Нм (5.2.16)
, Нм (5.2.16) , Нм (5.2.17)
, Нм (5.2.17)


 (5.2.18)
(5.2.18) <60мм условие прочности выполняется
<60мм условие прочности выполняется <50мм условие прочности выполняется
<50мм условие прочности выполняется (5.2.19)
(5.2.19) (5.2.20)
(5.2.20) , МПа (5.2.21)
, МПа (5.2.21) , МПа (5.2.22)
, МПа (5.2.22) ,мм3 (5.2.23)
,мм3 (5.2.23) ,мм3 (5.2.24)
,мм3 (5.2.24) (5.2.25)
(5.2.25)

 >
> 
 , так как S =
, так как S = 

 = 1,5,
= 1,5,

 >
>  (6.3)
(6.3)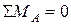
 (6.4)
(6.4)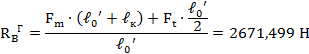
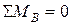
 (6.5)
(6.5)
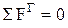 ;
; 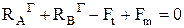
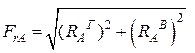 (6.6)
(6.6)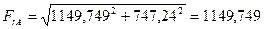 Н
Н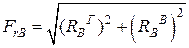 , Н (6.7)
, Н (6.7) Н
Н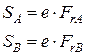 (6.8)
(6.8) и углу контакта a определяем коэффициент осевого нагружения е.
и углу контакта a определяем коэффициент осевого нагружения е.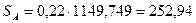

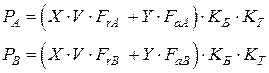 (6.9)
(6.9)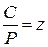 , где С – динамическая грузоподъемность подшипника.
, где С – динамическая грузоподъемность подшипника.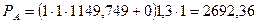 Н
Н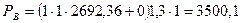 Н
Н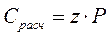 (6.10)
(6.10)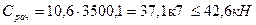
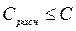
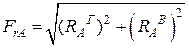 , Н (6.11)
, Н (6.11)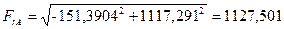 Н
Н Н
Н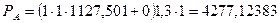 Н
Н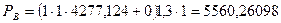 Н
Н