Файлы с плотным индексом, или индексно-прямые файлы

Рассмотрим файлы с плотным индексом. В этих файлах основная область содержит последовательность записей одинаковой длины, расположенных в произвольном порядке, а структура индексной записи в них имеет следующий вид:

	Значение ключа	Номер записи

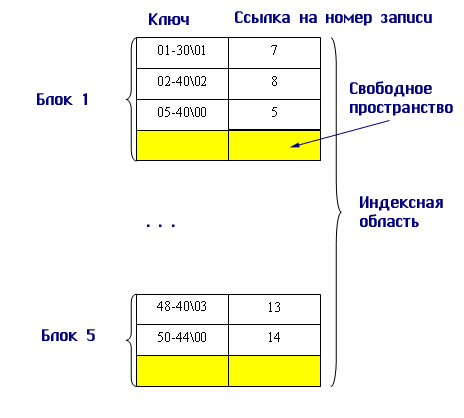
Здесь значение ключа — это значение первичного ключа, а номер записи — это порядковый номер записи в основной области, которая имеет данное значение первичного ключа.

Так как индексные файлы строятся для первичных ключей, однозначно определяющих запись, то в них не может быть двух записей, имеющих одинаковые значения первичного ключа. В индексных файлах с плотным индексом для каждой записи и основной области существует одна запись из индексной области. Все записи в индексной области упорядочены по значению ключа, поэтому можно применить более эффективные способы поиска в упорядоченном пространстве.

Длина доступа к произвольной записи оценивается не в абсолютных значениях, а в количестве обращений к устройству внешней памяти, которым обычно является диск. Именно обращение к диску является наиболее длительной операцией по сравнению со всеми обработками в оперативной памяти. Наиболее эффективным алгоритмом поиска на упорядоченном массиве является логарифмический, или бинарный, поиск. Очень хорошо изложил этот алгоритм барон Мюнхгаузен, когда он объяснял, как поймать льва в пустыне. При этом все пространство поиска разбивается пополам, и так как оно строго упорядочено, то определяется сначала, не является ли элемент искомым, а если пет, то в какой половине его надо искать. Следующим шагом мы определенную половину также делим пополам и производим аналогичные сравнения, и т. д., пока не обнаружим искомый элемент. Максимальное количество шагов поиска определяется двоичным логарифмом от общего числа элементов в искомом пространстве поиска:

Т_n = log₂N,

где N — число элементов.

Однако в нашем случае является существенным только число обращений к диску при поиске записи по заданному значению первичного ключа. Поиск происходит в индексной области, где применяется двоичный алгоритм поиска индексной записи, а потом путем прямой адресации мы обращаемся к основной области уже по конкретному номеру записи. Для того чтобы оценить максимальное время доступа, нам надо определить количество обращений к диску для поиска произвольной записи.

На диске записи файлов хранятся в блоках. Размер блока определяется физическими особенностями дискового контроллера и операционной системой. В одном блоке могут размещаться несколько записей. Поэтому нам надо определить количество индексных блоков, которое потребуется для размещения всех требуемых индексных записей, а потому максимальное число обращений к диску будет равно двоичному логарифму от заданного числа блоков плюс единица. Зачем нужна единица? После поиска номера записи в индексной области мы должны еще обратиться к основной области файла. Поэтому формула для вычисления максимального времени доступа в количестве обращений к диску выглядит следующим образом:

Т_n = log₂N_бл.инд. + 1.

Давайте рассмотрим конкретный пример и сравним время доступа при последовательном просмотре и при организации плотного индекса. Допустим, что мы имеем следующие исходные данные:

Длина записи файла (LZ) — 128 байт. Длина первичного ключа (LK) — 12 байт. Количество записей в файле (KZ) — 100000. Размер блока (LB) — 1024 байт.

Рассчитаем размер индексной записи. Для представления целого числа в пределах 100000 нам потребуется 3 байта, можем считать, что у нас допустима только четная адресация, поэтому нам надо отвести 4 байта для хранения номера записи, тогда длина индексной записи будет равна сумме размера ключа и ссылки на номер записи, то есть:

LI = LK + 4 = 14 + 4 = 16 байт.

Определим количество индексных блоков, которое требуется для обеспечения ссылок на заданное количество записей. Для этого сначала определим, сколько индексных записей может храниться в одном блоке:

KIZB = LB/LI = 1024/16 = 64 индексных записи в одном блоке. Теперь определим необходимое количество индексных блоков: KIB = KZ/KZIB = 100000/64 = 1563 блока.

Мы округлили в большую сторону, потому что пространство выделяется целыми блоками, и последний блок у нас будет заполнен не полностью.

А теперь мы уже можем вычислить максимальное количество обращений к диску при поиске произвольной записи:

Т_поиска ⁼ log₂KIB + 1 = log₂1563 + 1 = 11 + 1 = 12 обращений к диску.

Логарифм мы тоже округляем, так как считаем количество обращений, а оно должно быть целым числом.

Следовательно, для поиска произвольной записи по первичному ключу при организации плотного индекса потребуется не более 12 обращений к диску. А теперь оценим, какой выигрыш мы получаем, ведь организация индекса связана с дополнительными накладными расходами на его поддержку, поэтому такая организация может быть оправдана только в том случае, когда она действительно дает значительный выигрыш. Если бы мы не создавали индексное пространство, то при произвольном хранении записей в основной области нам бы в худшем случае было необходимо просмотреть все блоки, в которых хранится файл, временем просмотра записей внутри блока мы пренебрегаем, так как этот процесс происходит в оперативной памяти.

Количество блоков, которое необходимо для хранения всех 100 000 записей, мы определим по следующей формуле:

КВО = KZ/(LB/LZ) - 100000/(1024/128) - 12500 блоков.

И это означает, что максимальное время доступа равно 12500 обращений к диску. Да, действительно, выигрыш существенный.

Рассмотрим, как осуществляются операции добавления и удаления новых записей.

При операции добавления осуществляется запись в конец основной области. В индексной области необходимо произвести занесение информации в конкретное место, чтобы не нарушать упорядоченности. Поэтому вся индексная область файла разбивается на блоки и при начальном заполнении в каждом блоке остается свободная область (процент расширения) (рис. 9.7):

Рис. 9.7. Пример организации файла с плотным индексом

После определения блока, в который должен быть занесен индекс, этот блок копируется в оперативную память, там он модифицируется путем вставки в нужное место новой записи (благо в оперативной памяти это делается на несколько порядков быстрее, чем на диске) и, измененный, записывается обратно на диск. Определим максимальное количество обращений к диску, которое требуется при добавлении записи, — это количество обращений, необходимое для поиска записи плюс одно обращение для занесения измененного индексного блока и плюс одно обращение для занесения записи в основную область.

Т_{добавления} = log₂N + 1 + 1 + 1.

Естественно, в процессе добавления новых записей процент расширения постоянно уменьшается. Когда исчезает свободная область, возникает переполнение индексной области. В этом случае возможны два решения: либо перестроить заново индексную область, либо организовать область переполнения для индексной области, в которой будут храниться не поместившиеся в основную область записи. Однако первый способ потребует дополнительного времени на перестройку индексной области, а второй увеличит время на доступ к произвольной записи и потребует организации дополнительных ссылок в блоках па область переполнения.

Именно поэтому при проектировании физической базы данных так важно заранее как можно точнее определить объемы хранимой информации, спрогнозиро-вать ее рост и предусмотреть соответствующее расширение области хранения.

При удалении записи возникает следующая последовательность действий: запись в основной области помечается как удаленная (отсутствующая), в индексной области соответствующий индекс уничтожается физически, то есть записи, следующие за удаленной записью, перемещаются на ее место и блок, в котором хранился данный индекс, заново записывается па диск. При этом количество обращений к диску для этой операции такое же, как и при добавлении новой записи.

Файлы с неплотным индексом, или индексно-последовательные файлы

Попробуем усовершенствовать способ хранения файла: будем хранить его в упорядоченном виде и применим алгоритм двоичного поиска для доступа к произвольной записи. Тогда время доступа к произвольной записи будет существенно меньше. Для нашего примера это будет:

Т = log₂KBO = log₂12500 = 14 обращений к диску.

И это существенно меньше, чем 12 500 обращений при произвольном хранении записей файла. Однако и поддержание основного файла в упорядоченном виде также операция сложная.

Неплотный индекс строится именно для упорядоченных файлов. Для этих файлов используется принцип внутреннего упорядочения для уменьшения количества хранимых индексов. Структура записи индекса для таких файлов имеет следующий вид:

	Значение ключа первом записи блока	Номер блока с этой записью

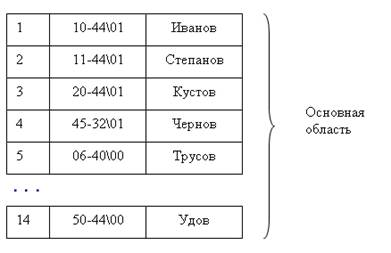
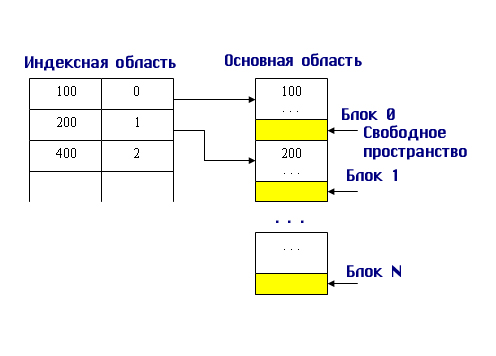
В индексной области мы теперь ищем нужный блок по заданному значению первичного ключа. Так как все записи упорядочены, то значение первой записи блока позволяет нам быстро определить, в каком блоке находится искомая запись. Все остальные действия происходят в основной области. На рис. 9.8 представлен пример заполнения основной и индексной областей, если первичным ключом являются целые числа.

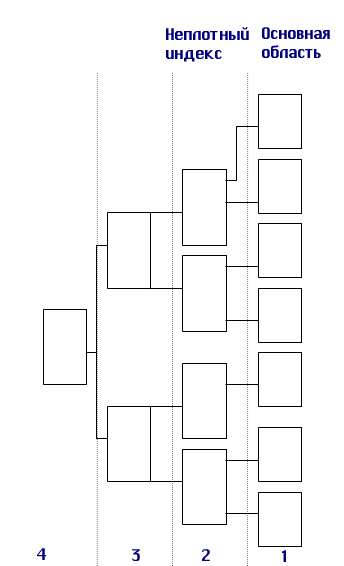
Рис. 9.8. Пример заполнения индексной и основной области при организации неплотного индекса

Время сортировки больших файлов весьма значительно, но поскольку файлы поддерживаются сортированными с момента их создания, накладные расходы в процессе добавления новой информации будут гораздо меньше. Оценим время доступа к произвольной записи для файлов с неплотным индексом. Алгоритм решения задачи аналогичен.

Сначала определим размер индексной записи. Если ранее ссылка рассчитывалась исходя из того, что требовалось ссылаться на 100000 записей, то теперь нам требуется ссылаться всего на 12 500 блоков, поэтому для ссылки достаточно двух байт. Тогда длина индексной записи будет равна:

LI = LK + 2 = 14 + 2 - 14 байт.

Тогда количество индексных записей в одном блоке будет равно:

KIZB = LB/LI = 1024/14 = 73 индексные записи в одном блоке.

Определим количество индексных блоков, которое необходимо для хранения требуемых индексных записей:

KIB = KBO/KZIB = 12500/73 = 172 блока.

Тогда время доступа по прежней формуле будет определяться:

Т_поиска = log₂KIB + 1 = log₂172 + 1=8+1=9 обращений к диску.

Мы видим, что при переходе к неплотному индексу время доступа уменьшилось практически в полтора раза. Поэтому можно признать, что организация неплотного индекса дает выигрыш в скорости доступа.

Рассмотрим процедуры добавления и удаления новой записи при подобном индексе.

Здесь механизм включения новой записи принципиально отличен от ранее рассмотренного. Здесь новая запись должна заноситься сразу в требуемый блок на требуемое место, которое определяется заданным принципом упорядоченности на множестве значений первичного ключа. Поэтому сначала ищется требуемый блок основной памяти, в который надо поместить новую запись, а потом этот блок считывается, затем в оперативной памяти корректируется содержимое блока и он снова записывается на диск на старое место. Здесь, так же как и в первом случае, должен быть задан процент первоначального заполнения блоков, но только применительно к основной области. В MS SQL server этот процент называется Full-factor и используется при формировании кластеризованных индексов. Кластеризованными называются как раз индексы, в которых исходные записи физически упорядочены по значениям первичного ключа. При внесении новой записи индексная область не корректируется.

Количество обращений к диску при добавлении новой записи равно количеству обращений, необходимых для поиска соответствующего блока плюс одно обращение, которое требуется для занесения измененного блока на старое место.

Т_{добавлений} ⁼ log₂N +1 + 1 обращений.

Уничтожение записи происходит путем ее физического удаления из основной области, при этом индексная область обычно не корректируется, даже если удаляется первая запись блока. Поэтому количество обращений к диску при удалении записи такое же, как и при добавлении новой записи.

Организация индексов в виде B-tree (В-деревьев)

Калькированный термин «В-дерево», в котором смешивается английский символ «В» и добавочное слово на русском языке, настолько устоялся в литературе, посвященной организации физического хранения данных, что я не решусь его корректировать.

Встретив как-то термин «B-дерево», я долго его трактовала, потому что привыкла уже к устоявшемуся обозначению. Поэтому будем работать с этим термином.

Построение В-деревьев связано с простой идеей построения индекса над уже построенным индексом. Действительно, если мы построим неплотный индекс, то сама индексная область может быть рассмотрена нами как основной файл, над которым надо снова построить неплотный индекс, а потом снова над новым индексом строим следующий и так до того момента, пока не останется всего один индексный блок.

Мы в общем случае получим некоторое дерево, каждый родительский блок которого связан с одинаковым количеством подчиненных блоков, число которых равно числу индексных записей, размещаемых в одном блоке. Количество обращений к диску при этом для поиска любой записи одинаково и равно количеству уровней в построенном дереве. Такие деревья называются сбалансированными (balanced) именно потому, что путь от корня до любого листа в этом древе одинаков. Именно термин «сбалансированное» от английского «balanced» — «сбалансированный, взвешенный» и дал название данному методу организации индекса.

Построим подобное дерево для нашего примера и рассчитаем для него количество уровней и, соответственно, количество обращений к диску.

На первом уровне число блоков равно числу блоков основной области, это нам известно, — оно равно 12 500 блоков. Второй уровень образуется из неплотного индекса, мы его тоже уже строили и вычислили, что количество блоков индексной области в этом случае равно 172 блокам. А теперь над этим вторым уровнем снова построим неплотный индекс.

Мы не будем менять длину индексной записи, а будем считать ее прежней, равной 14 байтам. Количество индексных записей в одном блоке нам тоже известно, и оно равно 73. Поэтому сразу определим, сколько блоков нам необходимо для хранения ссылок на 172 блока.

КIВ₃ = KIB₂/KZIB = 172/73 = 3 блока

Мы снова округляем в большую сторону, потому что последний, третий, блок будет заполнен не полностью.

И над третьим уровнем строим новый, и на нем будет всего один блок, в котором будет всего три записи. Поэтому число уровней в построенном дереве равно четырем, и соответственно количество обращений к диску для доступа к произвольной записи равно четырем (рис. 9.9). Это не максимально возможное число обращений, а всегда одно и то же, одинаковое для доступа к любой записи.

Т_д= R_уравн. =4

1 уровень 12500 блоков

2 уровень 172 блоков

3 уровень 3 блоков

4 уровень 1 блоков

Рис. 9.9. Построенное В-дерево

Механизм добавления и удаления записи при организации индекса в виде В-дерева аналогичен механизму, применяемому в случае с неплотным индексом.

И наконец, последнее, что хотелось бы прояснить, — это наличие вторых названий для плотного и неплотного индексов.

В случае плотного индекса после определения местонахождения искомой записи доступ к ней осуществляется прямым способом по номеру записи, поэтому этот способ организации индекса и называется индексно-прямым.

В случае неплотного индекса после нахождения блока, в котором расположена искомая запись, поиск внутри блока требуемой записи происходит последовательным просмотром и сравнением всех записей блока. Поэтому способ индексации с неплотным индексом называется еще и индексно-последовательным.

Моделирование отношений «один-ко-многим» на файловых структурах

Отношение иерархии является типичным для баз данных, поэтому моделирование иерархических связей является типичным для физических моделей баз данных.

Для моделирования отношений 1:М (один-ко-многим) и М:М (многие-ко-мно-гим) на файловых структурах используется принцип организации цепочек записей внутри файла и ссылки на номера записей для нескольких взаимосвязанных файлов.