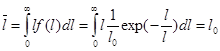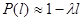Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики надёжности систем автомобиля.Содержание книги
Поиск на нашем сайте
Все системы автомобиля делятся на восстанавливаемые и невосстанавливаемые. Восстанавливаемые системы – в случае отказа подлежат восстановлению путем регулировок или других ремонтных воздействий. Невосстанавливаемые системы – могут иметь только один отказ, поскольку их восстановить невозможно или неэкономично. К характеристикам надёжности невосстанавливаемых систем относятся: Q(l) - вероятность отказа l – наработка P(l) – вероятность безотказной работы f(l) – частота отказов l(l) – интенсивность отказов
X-СВ, Х - значение которое принимает СВX
Вероятность того, что СВ X попадет в интервал dx
Вер { x < X < (x+dx) } = f(x)dx (1)
f(x) – пл. р. СВ
x X x+dx
а. Свойства плотности распределения 1. Неотрицательная
2. Не убывает 3. б. Второй важной характеристикой СВ является функция распределения F(x) равная вероятности того, что СВ Х не превзойдет конкретного значения х.
F(x) = Вер { X < x } т.е попадает на интервал от -
Если мы сможем записать какое-то конкретное выражение для функции F(x), значит мы будем знать закон распределения СВ. Чаще всего закон распределения СВ удаётся записать в том или ином виде если знать его характеристики - математическое ожидание (м.о.) - дисперсию СВ м.о.
дисперсия
 
Нормальный закон распределения:
f(x)=
Вероятность безотказной работы
Это вероятность того, что случайная наработка безотказной работы L, точно также не превзойдет конкретного значения е т.е. попадёт на интервал от 0 до е.
Вероятность безотказной работы
N (подконтрольных невосстанавливаемых систем) n(l) - отказы
Частота отказов
Это скорость изменения вероятности отказов.
По результатам статистических испытаний частота отказов выражается формулой:
Интенсивность отказа.
Пример: Взято под наблюдение 100 невосстанавливаемых систем. При наработке При наработке от
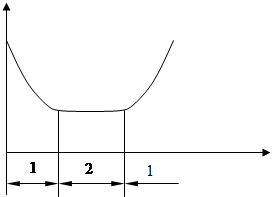
График интенсивности отказов.
Средняя наработка безотказной работы.
Связь между характеристиками надёжности Невосстанавливаемых систем.
 - (2) - (2)
Если надёжность системы рассматривается на 2-ом участке нормальной работы кривой интенсивности отказа, то λ=const, тогда
 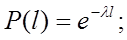 - (3) - (3)
Экспоненциальный закон надёжности.
где;
Обычно при решении практических задач интересной является область, где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.237.89 (0.009 с.) |

 l средняя наработка безотказной работы
l средняя наработка безотказной работы



 до х.
до х. (2)
(2) (3)
(3)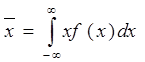 (4)
(4)





 e
e 


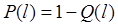
 - кривая убыли
- кривая убыли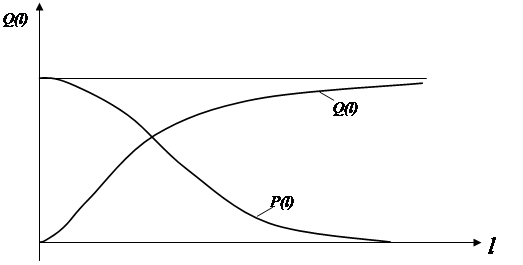



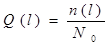

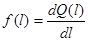 т.к.
т.к.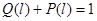

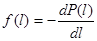
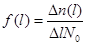
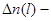 число систем отказавших в узком промежутке наработки
число систем отказавших в узком промежутке наработки 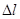 .
.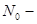 число систем первоначально поставленных под наблюдение.
число систем первоначально поставленных под наблюдение.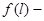 пл-ть распределения.
пл-ть распределения.

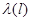 - это условная вероятность того, что элемент или система откажет в промежутке наработки
- это условная вероятность того, что элемент или система откажет в промежутке наработки  при условии, что на начало этого промежутка
при условии, что на начало этого промежутка 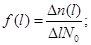
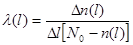 ;
; число систем отказавших при наработке
число систем отказавших при наработке  = 10 тыс. км. отказало
= 10 тыс. км. отказало  системы.
системы. = 15 тыс. км. отказало
= 15 тыс. км. отказало  системы. Определить интенсивность отказа в промежутке наработки
системы. Определить интенсивность отказа в промежутке наработки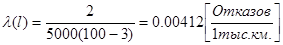 ;
; ;
На 2 участке работы, где интенсивность отказов постоянна, действует экспоненциальный закон надёжности.
;
На 2 участке работы, где интенсивность отказов постоянна, действует экспоненциальный закон надёжности.





 ;
;

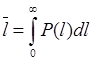

 , может называться и средней наработкой до первого отказа.
, может называться и средней наработкой до первого отказа.
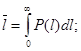 (1)
(1)
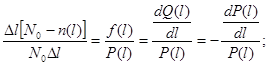
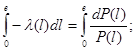

 Если наработка безотказной работы подчиняется экспоненциальному закону, то пл-ть распределения:
Если наработка безотказной работы подчиняется экспоненциальному закону, то пл-ть распределения: (1)
(1) - параметр экспоненциального закона.
- параметр экспоненциального закона. 
 При экспоненциальном законе надёжности вероятность отказа:
При экспоненциальном законе надёжности вероятность отказа: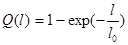 (2)
(2)
 (3)
(3)
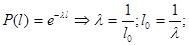

 - параметр является средней арифметической величиной.
- параметр является средней арифметической величиной.