
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о неинерциальных системах отсчета и силах инерцииСодержание книги
Поиск на нашем сайте
В класс механике рассматривается движение 𝓋≪С. При таких скоростях иетервалы времени м\у 2мя событиями в разных системах отсчета одинаковы ∆t=∆t*. Рассм 2 с-мы отсчета:а0=const; R=R*+r; d2R\dt2=d2R*dt2+d2r\dt2; a=a*+a0; ma=ma*+ma0; F=F*-Fin; F*=F-ma=F+Fin – з-н движения мат т-ки в неинерц с-ме отсчета. В неинерц с-ме отсчета на мат т-ку кроме силы F обусловленной действием на мат т-ку со стороны др тел возникает доп сила Fin = -ma0 наз-емая силой инерции. Силы инерции не подчиняются 3з-ну Ньютона. Они связаны с особенностью неинерц с-мой отсчета. Силы инерции схожи с силами тяжести, в нек-х случаях трудно различить. Что дает возможность второго объяснения движения тел в инерц с-ме отсчета. Принцип эквивалентности: инерц с-ма отсчета, в которой действует однородное поле тяготения сообщает всем телам ускорение а эквивалентна системе отсчета свободного от поля тяготения,но движущейся относительно инерц с-мы с ускорением –а.
16. Предмет мол ф-ки и т\д.Т\д параметры системы.Ид газ. Ур-е состояния ид газа. Мол физика -раздел ф-ки, изучающий св-ва тел и процессы протекающие в т\д системах на основе МКТ. МКТ базируется на 3осн положениях:1) все в-ва состоят из большого числа малых обособленных частиц молекул. 2) молекулы находятся в хаот движении 3) м\у молекулами действуют силы межмол взаимодействия Т\д изучает св-ва тел и процессы, но при этом она не затрагивает внут строение тел,изучает на основе энергетических позиций. Т\д параметры с-мы:Объем- часть пространства занимаемое системой. Давление -величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности. Р= Идеальный- газ у которого молекулы представляют из себя мат-е точки и силы взаимодействия м\у ними возникают только при непосредственном взаимодействии (соударении) молекул. Уравнение, связывающее р, T и V для данной массы газа называется уравнением состояния. f (Р,T,V) =0 Состояние газа однозначно определяется двумя любыми параметрами. Грамм- молекула (моль) вещества- такого количества вещества, масса которого в граммах равна молекулярной массе (μ), выраженной в частях массы молекулы углерода mc ⁄ 12. Число молей вещества в данной массе равно: N/NA= M/μèN= M/μ*NA.Тогда основное кинетическое уравнение представим в форме pV = M/μ N АkT.Получим уравнение состояния идеального газа в форме Менделеева - Клайперона. pV =M/μ RT 17. Осн ур-е МКТ ид газа для давления.МК толкование абсолютной т-ры. P=2\3nEпост=2\3n(m0Vкв)\2 осн ур МКт ид газов устанавливает связь микроскопических величин m0, Vкв смакроскопической величиной Р. Для одного моля газа:n= N A\V(кв); PVm=2\3 Na Е(пост)= RT; Е=3\2кТ.След-но, абс т-ра есть мера средней кинетической энергии поступательного движения молекулы. P=nkT
18. Скорости газовых молекул. Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная,средняя квадратичная и средняя арифметическая скорости молекул. Eпост=(m0Vкв)\2=3\2кТ; Vкв= Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)3/2 V2 exp(MV2/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, К;М - молярная масса, кг/моль.R = 8,3144 Дж/(моль•К) - универсальная газовая постоянная в системе СИ. VB= 19. Барометрическая формула. Распределение молекул в поле силы тяжести. Распределение Больцмана. Если бы молекулы газа не двигались хаотически, то под действием поля тяжести они бы скатились по поверхности земли. Если бы отсутствовало поле тяжести земли, то за счет хаотического движения молекулы газа разлетелись бы по мировому пространству. За счет действия 2ч противоположных процессов в газах устанавливается динамическое равновесие.В результате чего давление зем атмосферы с высотой будет убывать При dh>0, dP<0,dp=--ρgdh, ρ=μgp\rt. P=p0 Р=nkT; p0=n0kT;концентрация молекул зависит от их потенц энергии,чем >конц тем <энергия. Применительно к зем втмосфере с увеличением высоты следовало бы ожидать расслоение атм на отдельные компоненты. Опыты показывают что этого не происходит. g↓ с увеличением h,T↓ Больцман в ывел з-н по равномерному распределению энергии движения по мтепени=ям свободы молекул: для статистической системы в состоянии т\д равновесия на каждую степень поступ и вращательного движения в среднем приходится энергия тепового движения равная 1\2кТ, а на каждую степень колеб дв-я кТ.
20. Среднее число столкновений и средняя длина свободного пробега молекул. Зависимость средней длины свободного пробега молекул от давления и температуры. м\у 2мя последовательными сталкновениями солекулы движутся прямолинейно и равномерно и проходят путь наз длиной свободного пробега. Длина свободного пробега является случайной статической величиной,поэтому вводят величину наз средняя длина свободного пробег - расстояние к-е проходят большинство молекул м\у 2мя последовательными сталкновениями при данных усл. λ=
21. Явления переноса в газах.з-ны диффузии, внут трения и теплопроводности. Процесс перехода газа из неравновесного в равновесное состояние сопровождается переносом ряда физ величин(массы, импульса,кин эн),явления наз явлениями переноса: 1)диффузия- явление взаимного проникновения молекул в межмолек-е пространство контактирующих газов 𝒟(коэф диф-ии)=1\3 λ𝓋 2)внутреннее трение (вязкость) обусловлено появление сил трения м\у 2мя слоями газа,движущимися с различными скоростями. Это явление объясняется переносом импульса направленного движения хаотически движущимися и взаимодействующими молекулами.η(коэф вязкости)=1\3 ρλ𝓋 3 )Теплопроводность — перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения
22. Внутренняя энергия системы. Работа газа при изменениях его объема. Кол-во теплоты.1начало т\д. Внут энергия с-мы складывается из кин эн движения молекул, энергии покоя этих мол-л и потенц энергии взаимодействия м\у ними.Вн.эн с-мы яв-ся однозначной ф-ей ее состояния. Работа яв-ся количественной мерой убывания одной энергией и количественной мерой возрастания другой.A’=∆U, Q= ∆U В общем случае работа и теплообмен могут происходить одновременно ∆U= A’+ Q, А= -A’, ∆U= -A+ Q, Q= ∆U+А- мат выражение 1н т\д. кол-во теплоты сообщенное системе идет на увеличение ее внут энергии и на совершение работы системой против внеш сил. Для бесконечно малого процесса δQ=dU+δA
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.209 (0.005 с.) |

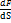 (Па ). Т-ра - величина пропорциональная кин энергии поступ движения(вМКТ) Т~Епост.в т\д-величина характеризующая направление теплопередачи или внут энергии.
(Па ). Т-ра - величина пропорциональная кин энергии поступ движения(вМКТ) Т~Епост.в т\д-величина характеризующая направление теплопередачи или внут энергии.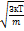 =
=  В молекулярном пучке имеются молекулы со всевозможными скоростями, как с маленькими так и с очень большими. Несмотря на полную хаотичность движения газ молекул и случайный хар-р столкновения их м\у собой распределение их по скоростям является не случайным,а вполне определенным. В состоянии т\д равновесия распределение молекул данного газа по скоростям является однозначным и единственно возможным,молекулы равномерно распределяются по направлениям скоростей и импульсов и статически по значениям скоростей и импульсов.
В молекулярном пучке имеются молекулы со всевозможными скоростями, как с маленькими так и с очень большими. Несмотря на полную хаотичность движения газ молекул и случайный хар-р столкновения их м\у собой распределение их по скоростям является не случайным,а вполне определенным. В состоянии т\д равновесия распределение молекул данного газа по скоростям является однозначным и единственно возможным,молекулы равномерно распределяются по направлениям скоростей и импульсов и статически по значениям скоростей и импульсов. =
=  ; V=
; V= 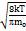 =
=  ; Vкв=
; Vкв=  = p0
= p0  с увеличением высоты давление ид газа убывает по
с увеличением высоты давление ид газа убывает по , где z-число столкновений, z=nπd2𝓋 если учесть движения всех молекул z=
, где z-число столкновений, z=nπd2𝓋 если учесть движения всех молекул z=  nπd2𝓋, тогда λ=
nπd2𝓋, тогда λ= 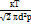 . Λзависит от: 1) если р=const, то наблюдается малая зависимость от т-ры,с повыш т-ры d↓ 2)если Т= const, то λ~
. Λзависит от: 1) если р=const, то наблюдается малая зависимость от т-ры,с повыш т-ры d↓ 2)если Т= const, то λ~  . С увеличением Р уменьшается расстояние.
. С увеличением Р уменьшается расстояние.


