Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
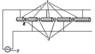
Момент сил, действующих на контур с током в магнитном поле.Содержание книги
Поиск на нашем сайте
Поместим в однородное магнитное поле с индукцией
Рис.9.2. Рамка с током в магнитном поле. Согласно закону Ампера, на каждый элемент тока рамки действует сила
Результирующая всех этих сил, как нетрудно убедиться, создает пару сил
где b – длинная сторона рамки ( Следовательно, можем написать:
где S = ab – площадь рамки. Учитывая, что магнитный момент рамки
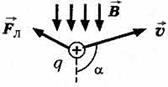
Действие магнитного поля на движущийся заряд. Сила Лоренца. Направление силы Лоренца. Траектория движения частицы, влетевшей перпендикулярно направлению магнитного поля и под произвольным углом. Ускорители заряженных частиц. Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q - заряд частицы;
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0, и заряд в магнитном поле движется равномерно и прямолинейно. Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной
и создает центростремительное ускорение равное
В этом случае частица движется по окружности.
Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение
тогда радиус окружности
а период обращения заряда в магнитном поле
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
Направление вектора силы Лоренца
При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы.
Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля (Рис. 89). Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля
из которого находим
Найдем период обращения частицы в магнитном поле
Из этой формулы следует интересный и неожиданный вывод[1] – период вращения частицы в магнитном поле не зависит от ее скорости. Частота вращения выражается формулой
и называется циклотронной частотой.
· Рис. 1 Механизм автофазировки · Рис. 10 Ускоритель Видероэ (схема) · Рис. 11 Резонатор линейного ускорителя (схематический разрез) Из 12 Ускорители заряженных частиц — устройства для получения заряженных частиц (электронов, протонов, атомных ядер, ионов) больших энергий. Ускорение производится с помощью электрического поля, способного изменять энергию частиц, обладающих электрическим зарядом. Магнитное поле может лишь изменить направление движения заряженных частиц, не меняя величины их скорости, поэтому в ускорителях оно применяется для управления движением частиц (формой траектории). Обычно ускоряющее электрическое поле создаётся внешними устройствами (генераторами). Но возможно ускорение с помощью полей, создаваемых др. заряженными частицами; такой метод ускорения называется коллективным (см. Ускорения заряженных частиц коллективные методы). У. з. ч. следует отличать от плазменных ускорителей, в которых происходит ускорение в среднем электрически нейтральных потоков заряженных частиц (плазмы).
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1021; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.01 с.) |

 плоский прямоугольный контур (рамку) с током (рис.9.2).
плоский прямоугольный контур (рамку) с током (рис.9.2).

 .
.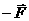 , стремящихся развернуть плоскость рамки перпендикулярно силовым линиям магнитного поля. Если a – короткая сторона рамки, то величина действующей на нее силы будет
, стремящихся развернуть плоскость рамки перпендикулярно силовым линиям магнитного поля. Если a – короткая сторона рамки, то величина действующей на нее силы будет 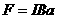 . Момент пары сил по величине равен:
. Момент пары сил по величине равен: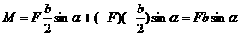 ,
, 
 - плечо силы F, α – угол между нормалью к плоскости рамки и силовой линией магнитного поля).
- плечо силы F, α – угол между нормалью к плоскости рамки и силовой линией магнитного поля).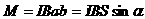 ,
,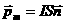 , последнюю формулу можно переписать в векторном виде:
, последнюю формулу можно переписать в векторном виде:

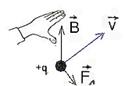






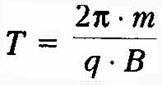
 определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.
определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.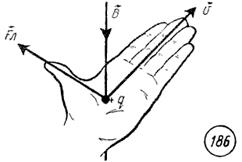

 , то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона
, то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона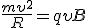 , (1)
, (1) . (2)
. (2)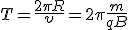 . (3)
. (3)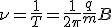 , (4)
, (4)