
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет дебита фильтрующейся жидкости для различных видов пористостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оценка дебита жидкости при линейном режиме равномерной фильтрации
Теория к разделу Рассмотрим случай субкапиллярной фильтрации, т.е. фильтрация равномерная и проходит через всю площадь образца, имеющего субкапиллярную пористость. Дебит жидкости при линейном режиме оценивается уравнением Дарси:
где kпр – проницаемость, Д; F – площадь фильтрации, см2; ∆P – перепад давления, атм; m – вязкость, спз; L – длина, см.
Типовая задача Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мД, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. Определить дебит жидкости.
Дано: kпр = 10 мД = 0,01 Д; F = 100 см2; ∆P/L = 0,25 атм/м = 0,0025 атм/см; m = 1 спз.
Найти: Q1
Решение:
Оценка дебита жидкости при неравномерно-проницаемой фильтрации
Теория к разделу Проницаемость жидкости при фильтрации через капилляр оцениваем из соотношения уравнений Дарси:
и Пуазейля:
откуда:
где kпр.кап – проницаемость при фильтрации жидкости через капилляр, Д; F – площадь фильтрации, см2; ∆P – перепад давления, атм; m – вязкость, спз; L – длина, см. После преобразования коэффициента проницаемости и радиуса капилляра к одной размерности получим эмпирическое уравнение для оценки коэффициента проницаемости при фильтрации жидкости через капилляр:
Типовая задача Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мДарси, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. В этом кубике существует один капилляр диаметром 0,2 мм. На сколько увеличится суммарный дебит при прочих равных параметрах m и ∆P/L?
Дано: Dк = 0,2 мм = 0,02 см; ∆P/L = 0,25 атм/м = 0,0025 атм/см; m = 1 спз; Nк =1.
Найти: Q2 - дебит при фильтрации через капилляр; Q3 - суммарный дебит за счёт субкапиллярной и капиллярной фильтрации.
Решение:
Рассчитаем дебит через этот капилляр:
По сравнению с субкапиллярной проницаемостью (kпр = 10 мД) дебит увеличится при наличии одного такого канала на 40% (Q2 / Q1), а если бы субкапиллярная проницаемость была kпр = 1 мД, то дебит увеличился бы на 400% (Q2 / Q1 × kпр). Оценка дебита жидкости при наличии трещиноватой фильтрации Теория к разделу Допустим, в кубике с субкапиллярной проницаемостью вместо канала имеется трещина вдоль всего образца шириной Lтр, высотой hтр. Оценить проницаемость трещины (щели) для жидкости, фильтрующейся через образец, можно, используя соотношение уравнений Буссинеска и Дарси:
где kпр.тр – проницаемость при наличии трещиноватой фильтрации, Д; v – линейная скорость движения жидкости, см/с; ∆P – перепад давления, атм; m – вязкость, спз; Lтр – ширина трещины, см; hтр – высота трещины, см. Приведя параметры к одной размерности в единицах измерения нефтепромысловой геологии, получим эмпирическое уравнение для оценки коэффициента проницаемости при трещиноватой фильтрации:
Типовая задача
Дан кубик породы размером 10х10х10 см, имеющий проницаемость 10 мДарси, через который фильтруется жидкость вязкостью 1 спз при градиенте давления (∆P/L), равном 0,25 атм/м. В этом кубике будет существовать одна трещина шириной 10 см, высотой 0,2 мм. На сколько увеличится суммарный дебит при прочих равных параметрах m и ∆P/L?
Дано: hтр = 0,2 мм = 0,02 см; ∆P/L = 0,25 атм/м =0,0025 атм/см; m = 1 спз; Lтр = 10 см; Мтр = 1.
Найти: Q4 - дебит при фильтрации через трещину; Q5 - суммарный дебит жидкости за счет субкапиллярной и трещиноватой фильтрации. Решение:
а суммарный дебит с учетом субкапиллярной фильтрации:
Сравнивая дебиты Q4 и Q1, получим, что наличие общей трещины приводит к увеличению дебита в 675 раз (1,688 / 0,0025).
3.4. Задания для самостоятельной работы
Дан кубик породы размером 10х10х10 см. Определить дебиты (Q1),(Q2),(Q3),(Q4),(Q5)при: 1. равномерной субкапиллярной и неравномерно-проницаемой фильтрациях; 2. равномерной субкапиллярной и трещиноватой фильтрациях и сравнить их для условий, представленных в таблице 3.1, имеющих следующие обозначения: kпр – проницаемость при субкапиллярной фильтрации, мД; m – вязкость жидкости, спз; ∆Р/L – перепад давления, атм/м; Nк – число капилляров; Dк – диаметр капилляра, мм; Lтр – длина трещин, см; hтр – высота трещины, мм; Мтр – число трещин; 1,..., 120 – номер варианта. Таблица 3.1
Продолжение табл. 3.1
Продолжение табл. 3.1
Продолжение табл. 3.1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.78.87 (0.008 с.) |

 , (3.1)
, (3.1) ,
, .
.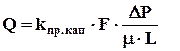 (3.2)
(3.2)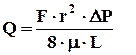 , (3.3)
, (3.3) , (3.4)
, (3.4)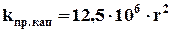 . (3.5)
. (3.5) ,
,
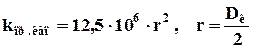 ,
, .
.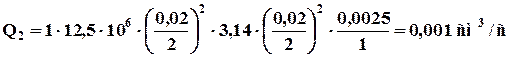 ,
, .
. , (3.6)
, (3.6) , (3.7)
, (3.7) . (3.8)
. (3.8) ,
, .
. ,
, .
.


