
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явление взаимоиндукции. Взаимная индуктивность.
Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. Индуктивность взаимная, величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура, то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2). Механические колебания. Механическими колебаниями называют движения тел, которые точно (или приблизительно) повторяются через равные промежутки времени. Примерами механических колебаний являются колебания математического или пружинного маятников. 1) сила, действующая на тело в любой точке траектории, направлена к положению равновесия, а в самой точке равновесия равна нулю; 2) сила пропорциональна отклонению тела от положения равновесия. Упругие волны. Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны. В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны. В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям. Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами. Длиной волны называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе λ=υT=υ/ν, где υ - скорость волны, T - период, ν - частота. Стоячие волны. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана. Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения. В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:
где u — возмущения в точке х в момент времени t, Интерференция света. Интерференция света — перераспределение интенсивности света в результате наложения(суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. Условия наблюдения интерференции Рассмотрим несколько характерных случаев: 1. Ортогональность поляризаций волн. При этом 2. В случае равенства частот волн 3. В случае 4. В случае
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.149 (0.006 с.) |
 ,
, — амплитуда стоячей волны,
— амплитуда стоячей волны, 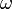 — частота, k — волновой вектор,
— частота, k — волновой вектор,  — фаза.
— фаза. и
и  . Интерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.
. Интерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы. и контраст полос не зависит от времени экспозиции
и контраст полос не зависит от времени экспозиции  .
. значение функции
значение функции  и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0
и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0 контраст полос существенным образом зависит от разности частот и времени экспозиции.
контраст полос существенным образом зависит от разности частот и времени экспозиции.


