
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Експлуатації та надійності машинСодержание книги Поиск на нашем сайте
Для дослідного визначення показників експлуатації та надійності машин проводиться спостереження за використанням чи експлуатацією
План оброблення цієї одновимірної статистичної сукупності наступний: 1. Первинне оброблення. 2. Знаходження числових характеристик емпіричного розподілу (середнє значення, медіана, середнє квадратичне відхилення, асиметрія, мода тощо). 3. Визначення параметрів узятого теоретичного розподілу. 4. Побудова за знайденими параметрами теоретичного розподілу. 5. Числове порівняння теоретичного розподілу з емпіричним за допомогою критеріїв узгодження. 6. Побудова графіків, емпіричного і теоретичного розподілу та їх порівняння. 7. Обчислення середніх помилок параметрів емпіричної сукупності. Первинне оброблення сукупності починається зі складання таблиці 1.2. У цій таблиці випадковою дискретною величиною є Емпірична ймовірність
Емпіричне значення функції розподілу випадкової величини
Кількість розрядів Широта розрядів однакова і визначається за формулою:
Наступна границя і – го інтервалу визначається як:
Таблиця 1.2 – Емпіричний розподіл
За даними таблиці 1.2 будують графіки розподілу статистичної ймовірності Рисунки 1.3 і 1.4 дають уявлення про можливий теоретичний закон розподілу випадкової величини t. Для використання цього закону необхідно вирахувати числові характеристики емпіричного розподілу, найважливішими з яких є: середнє значення
За характером графіка розподілу статистичної ймовірності (рис. 1.3) і числовими характеристиками цього розподілу вибирається функція розподілу напрацювання. Найчастіше це закон нормального розподілу, для якого щільність імовірності описується рівнянням:
У виразі (1.16) середнє квадратичне відхилення Обчислені величини Результати розрахунків заносять до таблиці 1.3. Таблиця 1.3
Для порівняння емпіричного значення
де Значення теоретичної функції розподілу
де За даними таблиці 1.3 будують теоретичний графік
При візуальному збігу цих графіків це необхідно довести. Для доведення використовується критерій А.Н. Колмогорова:
де Тут значення За критерієм Таблиця 1.4
Чим ближче Обчислення середніх помилок
де
Випадкові величини
Рекомендації щодо вибору вигляду функції розподілу Напрацювання (ресурсу)
Експоненціальний розподіл – для складних технічних систем і електродеталей, що не зазнають старіння та зносу. Щільність розподілу ймовірностей f(t):
ДМ – розподіл (дифузійний монотонний розподіл) – для механічних систем, двигунів машин і приладів, переважаючим механізмом відмов яких є не обернені процеси зносу, втоми, корозії:
де
ДN – розподіл (дифузійний немонотонний розподіл) для електрорадіовиробів електронних систем, а також технічних систем, що містять електровироби та механічні елементи, переважаючим механізмом відмов яких є процеси старіння, різні електричні процеси, а також процеси втоми:
Логарифмічно – нормальний розподіл – у випадку, коли основним типом зруйнування є втома, зумовлена періодичним процесом навантаження:
Розподіл Вейбула – для апроксимації розподілу напрацювання виробів, що не задовольняють вищеназваним:
Рекомендації щодо оцінювання параметра масштабу Параметри При відомому теоретичному законі розподілу чи отриманому експериментально, визначаються числові значення показників надійності за наведеною методикою.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.008 с.) |

 виробів у заданих умовах. При цьому визначається напрацювання виробів до відмови:
виробів у заданих умовах. При цьому визначається напрацювання виробів до відмови: ,
,  ,
,  ,
,  ,
,  .
.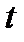 – напрацювання виробу в одиницях виміру роботи (год., км пробігу тощо) до виходу з ладу. Кількість виробів, що спостерігалися
– напрацювання виробу в одиницях виміру роботи (год., км пробігу тощо) до виходу з ладу. Кількість виробів, що спостерігалися  , а
, а  – що вийшли з ладу в і-му інтервалі.
– що вийшли з ладу в і-му інтервалі. .
. – кількість виробів, у котрих значення напрацювання до відмови.
– кількість виробів, у котрих значення напрацювання до відмови. визначається за формулою:
визначається за формулою: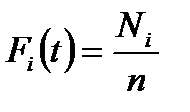 . (1.11)
. (1.11) призначається цілим числом і тим більшим, чим потрібні точніші результати.
призначається цілим числом і тим більшим, чим потрібні точніші результати. .
. , (1.12)
, (1.12)

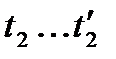
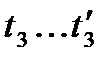





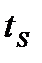

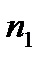



















 (рис. 1.3) і функції розподілу F(t) (рис. 1.4).
(рис. 1.3) і функції розподілу F(t) (рис. 1.4). і середнє квадратичне відхилення
і середнє квадратичне відхилення  :
: , (1.14)
, (1.14) , (1.15)
, (1.15) . (1.16)
. (1.16) визначається за формулою (1.15), а середнє значення
визначається за формулою (1.15), а середнє значення  – за формулою (1.14).
– за формулою (1.14). і
і  підставляються до рівняння (1.16), за яким виконуються розрахунки для побудови теоретичного розподілу.
підставляються до рівняння (1.16), за яким виконуються розрахунки для побудови теоретичного розподілу.
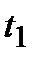











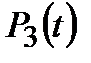











 і теоретичного
і теоретичного  останнє визначається за формулою:
останнє визначається за формулою: , (1.17)
, (1.17) – ширина інтервалу за вихідними даними.
– ширина інтервалу за вихідними даними. :
: , (1.18)
, (1.18) – теоретичне число об’єктів (автомобілів), у яких значення випадкової величини
– теоретичне число об’єктів (автомобілів), у яких значення випадкової величини  .
.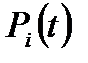 на рисунку 1.7 для порівняння з експериментальним.
на рисунку 1.7 для порівняння з експериментальним.
 , (1.19)
, (1.19) .
. беруть з таблиці 1.1, а значення
беруть з таблиці 1.1, а значення  – з таблиці 1.3.
– з таблиці 1.3. за допомогою таблиці 1.4 знаходиться величина
за допомогою таблиці 1.4 знаходиться величина  , що дорівнює ймовірності того, що різниця D перевищує отримане значення.
, що дорівнює ймовірності того, що різниця D перевищує отримане значення.

 до одиниці, тим краще прийнятий теоретичний розподіл зображує емпіричний. При
до одиниці, тим краще прийнятий теоретичний розподіл зображує емпіричний. При  можна вважати вибраний теоретичний закон адекватним.
можна вважати вибраний теоретичний закон адекватним. параметрів
параметрів  і
і  виконується за формулами:
виконується за формулами: ,
,  ,
, – середнє квадратичне відхилення;
– середнє квадратичне відхилення; – кількість об’єктів, що досліджується.
– кількість об’єктів, що досліджується.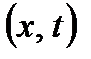 можуть підлягати різним законам розподілу: Гаусса, Вейбулла, Релея тощо.
можуть підлягати різним законам розподілу: Гаусса, Вейбулла, Релея тощо.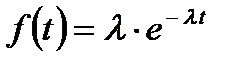 , (1.21)
, (1.21)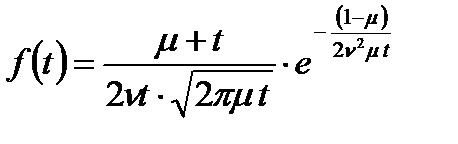 , (1.22)
, (1.22) – параметр масштабу;
– параметр масштабу; – параметр форми;
– параметр форми;  ;
;  .
. . (1.23)
. (1.23) . (1.25)
. (1.25) закону розподілу напрацювання (ресурсу):
закону розподілу напрацювання (ресурсу):  і
і  – відомі параметри за прототипом; для (1.21)
– відомі параметри за прототипом; для (1.21)  ; для (1.22), (1.23) і (1.24)
; для (1.22), (1.23) і (1.24)  ; для (1.25)
; для (1.25)  ;
;  – для однотипних об’єктів, що знаходяться в різних умовах;
– для однотипних об’єктів, що знаходяться в різних умовах;  – для однотипних об’єктів, що знаходяться в різних умовах;
– для однотипних об’єктів, що знаходяться в різних умовах;  однотипних об’єктів, що знаходяться в однакових умовах, зі вжитими заходами з підвищення надійності.
однотипних об’єктів, що знаходяться в однакових умовах, зі вжитими заходами з підвищення надійності. ,
,  і
і  повинні бути відомі, визначаються за аналогами чи експериментальними даними.
повинні бути відомі, визначаються за аналогами чи експериментальними даними.


