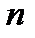Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практичні заняття і контрольні роботиСодержание книги Поиск на нашем сайте
Мета пропонованих практичних занять і контрольних завдань полягає у засвоєнні студентами методів визначення числових значень показників надійності машин, а також параметрів, що характеризують їх експлуатаційні властивості, вивченні розрахунків зносу типових конструкцій деталей машин, а також прищепити майбутньому фахівцеві навички визначати оптимальний строк служби машин з метою своєчасного призначення процедури технічного обслуговування і ремонту. Для задачі № 1 варіанти завдань знаходяться в таблицях 2.5 та 2.6, для задачі № 2 – у таблицях 2.7 та 2.8, для задачі № 3 – у вигляді таблиці 2.9, а для задачі № 4 – у вигляді таблиць 2.10 та 2.11. Вибір свого варіанта завдання студент здійснює за двома останніми цифрами залікової книжки. Вказівки щодо вибору початкових даних містяться в кінці даного розділу. У контрольній роботі студент виконує чотири задачі відповідно до свого варіанта. Контрольна робота для студентів заочної форми навчання виконується на зброшурованих аркушах формату А 4 із дотриманням вимог стандартів для текстових документів. Креслення, графіки і розрахункові схеми мають бути виконані олівцем. На першій сторінці роботи обов'язково вказується шифр залікової книжки студента.
Задача № 1 Завдання до задачі № 1 1. За заданою таблицею 2.1 після перетворень емпіричного розподілу термінів служби автомобіля t побудувати графіки: - розподілу ймовірності безвідмовної роботи Р(t); - функції розподілу (імовірності виникнення відмови) F(t)); - імовірності безвідмовної роботи P(t). 2. Визначити числові значення показників надійності: - середнє напрацювання до відмови tсер; - інтенсивність відмов - імовірність безвідмовної роботи - гамма-процентний ресурс 3. За побудованим многокутником розподілу (імовірності
Приклад розв’язання задачі
У таблиці 2.1 наведено емпіричний розподіл термінів служби автомобілів визначеної марки у тисячах кілометрах пробігу до капітального ремонту. За наведеним емпіричним розподілом розв'язати поставлену задачу.
Таблиця 2.1 – Емпіричний розподіл термінів служби автомобілів t (у тисячах кілометрах пробігу) до першого капітального ремонту
Розв'язання У таблиці 2.1 випадковою дискретною величиною є термін служби автомобіля t у тисячах кілометрах пробігу. З урахуванням цього таблицю 2.1 пере- творюємо на таблицю 2.2. У таблиці 2.2 загальна кількість спостережуваних автомобілів визначається за наступною формулою:
де ni – кількість об'єктів, що втратили працездатність в i -му інтервалі пробігу; S – кількість інтервалів, на які розділений пробіг. Таблиця 2.2
Емпірична ймовірність для певного інтервалу визначається за формулою:
де n – загальна кількість об'єктів в експерименті. Наприклад, для першого інтервалу пробігу емпірична ймовірність визначатиметься наступним чином:
Аналогічним чином визначаються числові значення pi(t) для кожного інтервалу пробігу та отримані результати вносять до таблиці 2.2. N – теоретична кількість об'єктів, у яких значення випадкової величини t Ni=Ni-l+ni-l. (2.3) Аналіз умови t < ti дозволяє зробити висновок, що
Аналогічним чином визначаються всі наступні значення теоретичного числа об'єктів Емпіричне значення функції розподілу випадкової величини t визначається за формулою:
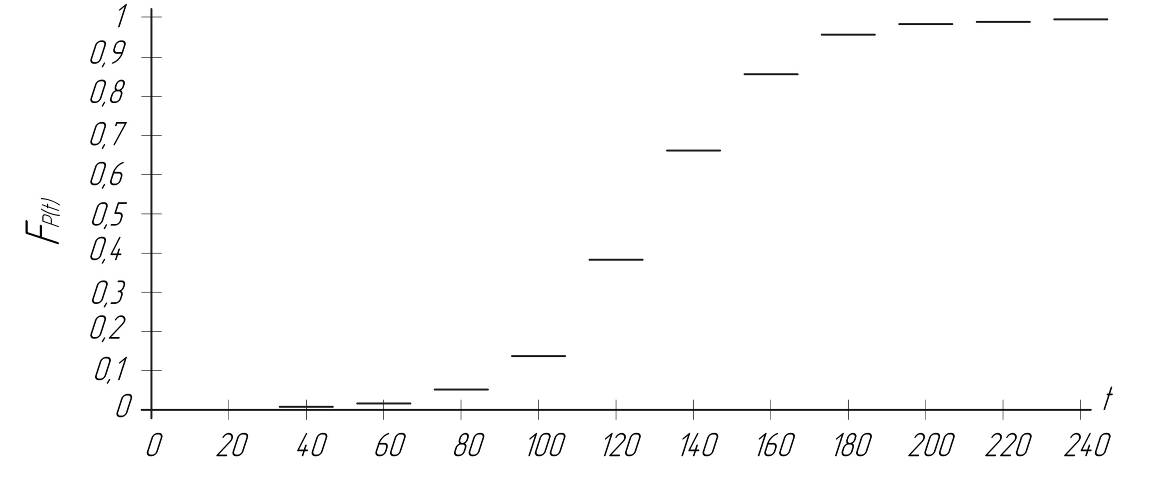
Отримані чисельні значення функції розподілу випадкової величини За даними таблиці 2.2 будують графіки розподілу ймовірності p(t) (рис. 2.1) і функції розподілу F(t) (рис. 2.2). Аналіз графічної інтерпретації графіка, що наведено на рис. 2.2, дозволяє зробити висновок, що зі збільшенням величини напрацювання імовірність виникнення відмови збільшується. За даними таблиці 2.2 визначаються чисельні значення показників надійності виробу.
Рисунок 2.1 – Розподіл імовірності відмови 1 – багатокутник розподілу; 2 – крива нормального розподілу
Рисунок 2.2 – Функція розподілу (імовірність виникнення відмови)
Середнє напрацювання до відмови tсер є математичним очікуванням пробігу автомобіля до першої або наступної відмови аналізованого виду. Статистично цей показник надійності визначається відношенням суми пробігів випробуваних автомобілів, якщо всі вони відмовили за час випробувань до кількості автомобілів
де ti – пробіг до відмови 1-го автомобіля (середина інтервалу у тисячах кілометрах пробігу). Примітка. У розглянутій задачі даний розподіл термінів служби автомобіля З урахуванням даних задачі, що будуть наведені нижче, формула для визначення середнього наробітку на відмову набуде наступного вигляду:
Перетворення формули (2.5) у формулу (2.6) пов'язане з тим, що в наведеній задачі наведено дев’ять інтервалів, у яких в одному інтервалі втрачає працездатність декілька машин, а сума їх за дев’ять інтервалів дорівнює п. Інтенсивністю потоку відмови називають умовну ймовірність виникнення відмови не відновлюваного об'єкта, зумовлену для аналізованого моменту часу за умови, що до цього моменту відмова не виникла і визначається за наступною формулою:
де n(t) – кількість об'єктів, у яких термін служби t > ti, тобто кількість технічних об'єктів, що залишилися працездатними до кінця напрацювання;
Візьмемо, t=
У цьому випадку:
Імовірність безвідмовної роботи визначає ймовірність того, що в межах заданого пробігу автомобіля відмова визначеного виду не виникне. Імовірність безвідмовної роботи статистично оцінюється відношенням працездатних елементів наприкінці n(t) і на початку n цього пробігу:
Наприклад, для середини інтервалу t = 40 тисяч кілометрів значення n(t) визначатиметься наступним чином:
Тоді:
Аналогічно визначаються всі значення P(t) для усіх інтервалів пробігу та за отриманими даними будується графік імовірності безвідмовної роботи P(t), загальний вигляд якого наведено на рис. 2.3. Гамма – процентним ресурсом
Рисунок 2.3 – Імовірність безвідмовної роботи Наприклад,
Визначивши таким чином значення За графіком імовірності безвідмовної роботи (рис. 2.3) знаходиться значення Таким чином у результаті проведення експериментальних досліджень були визначені наближеним методом показники надійності машин. Для уточнення отриманих показників надійності машин використовують закони розподілу випадкових величин, рекомендації стосовно вибору яких наведено в [4]. У даному випадку для опису розподілу випадкової величини t використовується закон нормального (Гауссового) розподілу випадкової величини, як найбільш поширений і природній закон розподілу. Закон нормального розподілу щільності ймовірності визначається за наступною формулою:
де f(t) – щільність імовірності випадкової величини t;
e = 2,71 – основа натурального логарифма. Для використання залежності (2.10) необхідно визначити наступні параметри: середнє напрацювання на відмову t за даними таблиці 2.2 визначається за формулою:
Наприклад:
Після цього проводиться порівняння значення t, отриманого за формулами (2.6) і (2.11). Отримані числові значення t повинні збігатися. Середнє квадратичне відхилення
Обчислені числові величини t і Наприклад, для першої середини інтервалу розглянутого пробігу функція щільності ймовірності випадкової величини визначатиметься наступним чином:
Аналогічним чином визначатимуться всі наступні числові значення fi(t). Отримані результати заносять до таблиці 2.3. Теоретичне значення ймовірності безвідмовної роботи
Наприклад:
Аналогічним чином визначатимуться наступні числові значення Після визначення теоретичної ймовірності безвідмовної роботи Значення теоретичного числа об'єктів, що втратили працездатність у кожному конкретному інтервалі, визначається за формулою:
Наприклад:
Аналогічним чином визначаються наступні числові значення
Таблиця 2.3 – Дані для побудови теоретичного закону розподілу
Теоретичне число об'єктів (автомобілів), у яких значення випадкової величини t <
Числові значення
Аналогічно визначаються всі значення Наступним етапом виконання досліджень є порівняння теоретичних і практичних результатів. Порівняння можна проводити візуально і за критерієм згоди. При візуальному порівнянні проводиться аналіз збігу багатокутника розподілу ймовірності безвідмовної роботи з теоретичною кривою закону нормального розподілу. Між емпіричним і теоретичним розподілами можливі деякі візуальні розбіжності. Тому для остаточного доведення узгодженості теоретичних і експериментальних результатів використовуються спеціальні критерії згоди. Найбільш поширеним є критерій згоди А.М. Колмогорова. Цей критерій дає завищене значення ймовірності згоди, але він простіше деяких інших критеріїв. Критерій згоди A.M. Колмогорова – це максимальна різниця розбіжності теоретичних та експериментальних результатів, а саме:
де Критерій згоди D визначається для кожного інтервалу за формулою (2.17) наступним чином:
Аналогічно визначаються всі наступні значення Dі. Із отриманих числових значень D згідно з умовою (2.17) вибирається тільки одне – максимальне. Визначаємо максимальне значення Di. Максимальним значенням буде D4, яке дорівнює:
Визначаємо критерій
За критерієм
Таблиця 2.4
Чим більше наближене числове значення P( Отже, за даними таблиці 2.4 Р( Середні помилки параметрів
Відповідно до теоретичного закону розподілу щільності ймовірності (2.10) визначаються значення показників надійності для виробів, що досліджуються, точним методом: · середнє напрацювання на відмову:
· імовірність безвідмовної роботи до напрацювання
· інтенсивність відмов:
Задача № 2 Завдання до задачі №2 1. Визначити надійність (імовірність безвідмовної роботи) 2. Розв'язати запропоновану задачу оберненим способом, тобто визначити потрібну ймовірність безвідмовної роботи Pi(t) деталей машин, якщо відоме числове значення сумарної ймовірності безвідмовної роботи
Приклад розв’язання задачі Дано: m = 10, n = 2, Pi(t) = 0,95, За вихідними даними будуються схеми з'єднань деталей машин таким чином, як це показано на рис. 2.4 – 2.7. 1. Для послідовного з'єднання деталей імовірність безвідмовної роботи
2. Для паралельного з'єднання деталей імовірність безвідмовної роботи
Рис. 2.4 – Послідовне з'єднання деталей
Рис. 2.5 – Паралельне з'єднання деталей
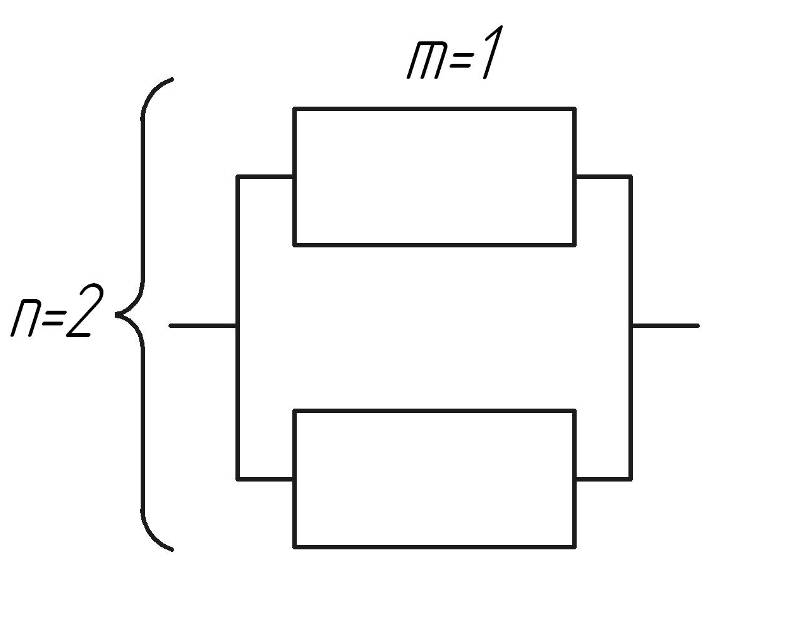
Рис. 2.6 – Змішане з'єднання деталей із загальним резервуванням
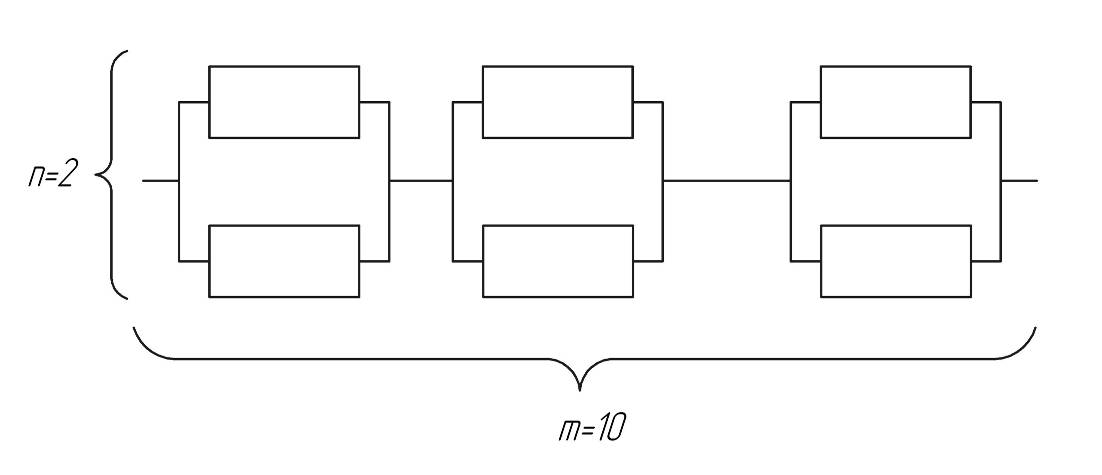
Рис. 2.7 – Змішане з'єднання деталей з роздільним резервуванням
3. Для змішаного з'єднання деталей із загальним резервуванням імовірність безвідмовної роботи
Наприклад:
4. Для змішаного з'єднання деталей з роздільним резервуванням імовірність безвідмовної роботи
Наприклад:
Для розв’язування оберненої задачі формули (2.21 – 2.24) необхідно перетворити відносно Pi(t) за ними виконати розрахунки. 1. Для послідовного з'єднання деталей імовірність безвідмовної роботи Pi(t) деталей машин визначатиметься за формулою:
Наприклад:
2. Для паралельного з'єднання деталей імовірність безвідмовної роботи Pi(t) деталей машин визначатиметься за формулою:
Наприклад:
3. Для змішаного з'єднання деталей із загальним резервуванням імовірність безвідмовної роботи Pi(t) деталей машин визначатиметься за формулою:
Наприклад:
4. Для змішаного з'єднання деталей із роздільним резервуванням імовірність безвідмовної роботи Pi(t) деталей машин визначатиметься за формулою:
Наприклад:
Задача № 3 Завдання до задачі № 3 За експериментальними даними експлуатації автомобіля ГАЗ-24 розрахувати його пробіг до зносу ресурсу накладок зчеплення. Приклад розв’язання задачі Пробіг автомобіля до зносу ресурсу накладок щеплення визначається за наступною формулою:
де j1 ,2...n – зносостійкість, отримана експериментальним шляхом, для відповідних умов експлуатації, кгс·м/см2·мм; аэкв 1,2… n – питома робота сили тертя на 1 км пробігу автомобіля у відповідних умовах експлуатації, кгс·м/см2; dL - частка пробігу автомобіля за відповідних умов експлуатації у сотих частках відсотка. Значення допустимої величини сумарного зносу накладок Примітка. Оскільки, згідно з двома останніми цифрами залікової книжки, студент вибирає тільки дві умови експлуатації, то частка пробігу автомобіля dL складає 50 %, або у відносних одиницях виміру 0,5. Останнє числове значення dL і буде підставлене до формули (2.29). Задача № 4 Завдання до задачі № 4 Розрахувати середню величину, зносу U напрямних станин верстатів за задану певну кількість років. Приклад розв’язання задачі Верстати працюють на двох режимах - робочому (і=1) та холостому (і=2) ходах. Базовий режим – робочий. Середня величина зносу розраховується за наступною формулою:
де k1 і k2 – коефіцієнти, що враховують режим роботи верстата; I – питома інтенсивність зносу при базовому режимі роботи, мкм·см2/кгс·км; Pi, – номінальний середній тиск при i -му режимі, кгс/см2;
L – загальний сумарний шлях тертя. При розв’язанні задачі беремо, k1 = k2 =2. Загальний сумарний шлях тертя L визначається за наступною залежністю:
де LГ – сумарний річний шлях тертя; n – кількість років роботи. При двозмінній роботі LГ – 1,1 км/рік. Поправкові коефіцієнти
де L1 та L2 - шляхи тертя на різних режимах. При розв’язанні задачі беремо L1 = L2 = 0,5. Вихідні дані до задач Вихідні дані до задачі №1 Вибір свого варіанта завдання виконується за таблицями 2.5 та 2.6. За передостанньою цифрою шифру за таблицею 2.5 студент вибирає межі інтервалів пробігу і значення наробітку Таблиця 2. 5
За останньою цифрою шифру за таблицею 2.6 студент вибирає варіант емпіричного розподілу термінів служби (кількість технічних об'єктів, що втратили працездатність в конкретному інтервалі) і значення ресурсу Таблиця 2.6
Вихідні дані до задачі № 2 Вибір свого варіанта завдання виконується за даними, що наведені таблицях 2.7 та 2.8. За передостанньою цифрою шифру за таблицею 2.7 студент вибирає значення ймовірності безвідмовної роботи Р(t) деталей машини. За останньою цифрою шифру за таблицею 2.8 студент вибирає числові значення показників m і n.
Таблиця 2.7
Таблиця 2.8
Вихідні дані до задачі № 3 Відповідно до передостанньої та останньої цифри шифру студент, за даними таблиці 2.9, вибирає два варіанти умов експлуатації автомобіля. При цьому для кожного варіанта експлуатації беремо d1 = 50% (d1 = 0,5). Розрахунок пробігу ведеться для певних умов експлуатації. Таблиця 2.9 – Дані експлуатації автомобіля у різних умовах
Вихідні дані до задачі № 4 Відповідно до передостанньої цифри шифру студент за даними, що наведені в таблиці 2.10 вибирає тип верстата. За останньою цифрою шифру студент за даними, що наведені в таблиці 2.11, вибирає кількість років роботи n і співвідношення коефіцієнтів тертя f2/f1. Таблиця 2.10
Таблиця 2.11
ПИТАННЯ ДО САМОПІДГОТОВКИ ТА ТЕСТИ З ДИСЦИПЛІНИ
Наведені питання є теоретичною основою для вивчення організації, експлуатації, технічного обслуговування і ремонту машин різного призначення в спеціальних курсах. Питання, що наведені тут, охоплюють повний програмний курс дисципліни. На кожне питання подано три правдоподібні відповіді, але правильною є одна. Правильні відповіді наводяться в окремому розділі. Така методика дозволяє глибше і надійніше освоїти матеріал при самостійному його вивченні. На основі питань складено тести трьох рівнів. Перший рівень – це тест за першу половину курсу, другий – це тест за другу половину курсу і третій – це тест за весь курс. Білети тестів 1-го і 2-го рівнів мають три питання, а білети 3-го рівня – шість питань. Правильні відповіді на питан
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.119 (0.011 с.) |

 для напрацювання
для напрацювання  ;
; для напрацювання у
для напрацювання у  ;
; .
. ) установити імовірний вид теоретичного закону розподілу (розподілу щільності ймовірності f(t)), а за емпіричним розподілом термінів служби машини визначити числові значення параметрів теоретичного закону розподілу.
) установити імовірний вид теоретичного закону розподілу (розподілу щільності ймовірності f(t)), а за емпіричним розподілом термінів служби машини визначити числові значення параметрів теоретичного закону розподілу.
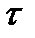 = 100 тис. км;
= 100 тис. км;  = 70%
= 70%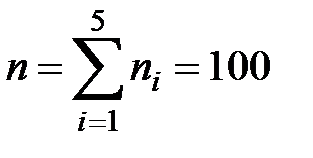 , (2.1)
, (2.1)

 , (2.2)
, (2.2)
 ti. Числове значення величини
ti. Числове значення величини  визначається за формулою:
визначається за формулою: . Наступні числові значення N визначатимуться за формулою (2.3). Указане дозволяє отримати наступне:
. Наступні числові значення N визначатимуться за формулою (2.3). Указане дозволяє отримати наступне:

 (2.4)
(2.4) вносять до таблиці 2.2.
вносять до таблиці 2.2.
 :
: (2.5)
(2.5) у тисячах кілометрах пробігу до першого капітального ремонту і визначається конкретним напрацюванням
у тисячах кілометрах пробігу до першого капітального ремонту і визначається конкретним напрацюванням 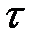 . Але різна кількість автомобілів може втратити працездатність як до кінця напрацювання
. Але різна кількість автомобілів може втратити працездатність як до кінця напрацювання  , так і продовжувати працювати далі. Середини інтервалів, у котрих деяка кількість машин втрачає працездатність, позначається через
, так і продовжувати працювати далі. Середини інтервалів, у котрих деяка кількість машин втрачає працездатність, позначається через  .
.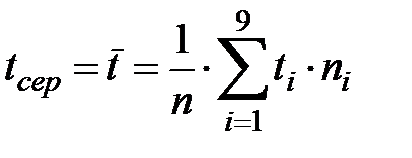 . (2.6)
. (2.6) (2.7)
(2.7)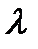 (t) – умовна імовірність виникнення відмови в момент пробігу t=
(t) – умовна імовірність виникнення відмови в момент пробігу t= 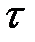 за умови, що до цього проміжку часу об'єкт був справний;
за умови, що до цього проміжку часу об'єкт був справний; t – ширина інтервалу у тисячах кілометрах.
t – ширина інтервалу у тисячах кілометрах.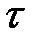 = 100 тисяч кілометрів пробігу, а
= 100 тисяч кілометрів пробігу, а  t =20 тисяч кілометрів (табл.. 2.1). Згідно з визначенням n(t),отримаємо наступне:
t =20 тисяч кілометрів (табл.. 2.1). Згідно з визначенням n(t),отримаємо наступне:

 .
. (2.8)
(2.8)

 називається напрацювання, протягом якого об'єкт не досягне граничного стану з даною ймовірністю
називається напрацювання, протягом якого об'єкт не досягне граничного стану з даною ймовірністю 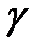 , заданою у відсотках. Імовірність
, заданою у відсотках. Імовірність 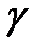 – відсотків фактично є імовірністю безвідмовної роботи до граничного стану:
– відсотків фактично є імовірністю безвідмовної роботи до граничного стану: (2.9)
(2.9)

 ,відкладаємо його на вертикальній осі графіка ймовірності безвідмовної роботи (рис. 2.3). Проводиться горизонтальна лінія до перетину з кривою графіка, що дозволяє отримати на графіку точку. Опускаючи із отриманої точки перпендикуляр на горизонтальну вісь знаходиться певне числове значення
,відкладаємо його на вертикальній осі графіка ймовірності безвідмовної роботи (рис. 2.3). Проводиться горизонтальна лінія до перетину з кривою графіка, що дозволяє отримати на графіку точку. Опускаючи із отриманої точки перпендикуляр на горизонтальну вісь знаходиться певне числове значення  .
.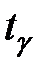 = 95 тис. км, тобто t70 = 95 тис. км.
= 95 тис. км, тобто t70 = 95 тис. км. (2.10)
(2.10) – середнє значення (математичне очікування) наробітки на відмову;
– середнє значення (математичне очікування) наробітки на відмову; – середнє квадратичне відхилення;
– середнє квадратичне відхилення; (2.11)
(2.11)
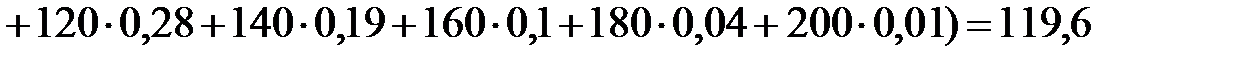 тис. км.
тис. км. обчислюється за формулою:
обчислюється за формулою: (2.12)
(2.12)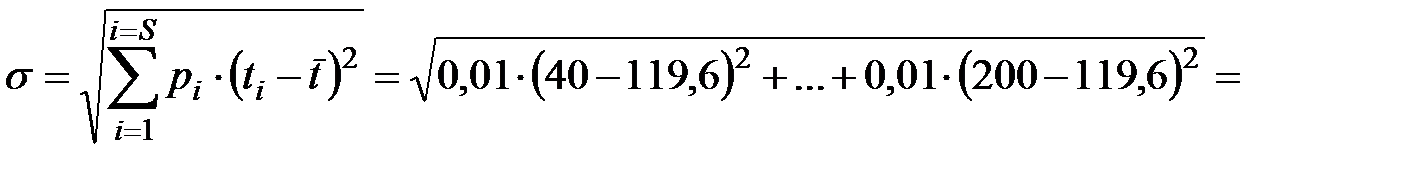
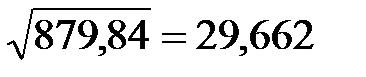 тис. км.
тис. км. підставляються до закону нормального розподілу (2.10), за яким виконуються розрахунки для побудови теоретичного розподілу.
підставляються до закону нормального розподілу (2.10), за яким виконуються розрахунки для побудови теоретичного розподілу.
 визначається за формулою:
визначається за формулою: (2.13)
(2.13)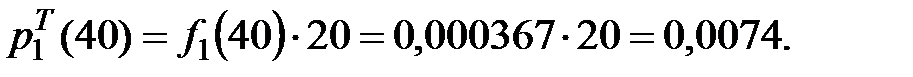
 . Отримані результати заносяться в таблицю 2.3.
. Отримані результати заносяться в таблицю 2.3. на багатокутник розподілу випадкової величини, графічну інтерпретацію якого зображено на рис. 2.1, наносяться числові значення
на багатокутник розподілу випадкової величини, графічну інтерпретацію якого зображено на рис. 2.1, наносяться числові значення  для кожної середини інтервалу із таблиці 2.3. Отримані точки поєднуються між собою плавною кривою лінією (крива 2 на рис. 2.1).
для кожної середини інтервалу із таблиці 2.3. Отримані точки поєднуються між собою плавною кривою лінією (крива 2 на рис. 2.1). (2.14)
(2.14)
 для кожного конкретного інтервалу. Отримані результати заносяться до таблиці 2.3.
для кожного конкретного інтервалу. Отримані результати заносяться до таблиці 2.3.




 обчислюється за формулою:
обчислюється за формулою: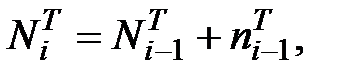 (2.15)
(2.15)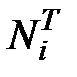 визначаються саме таким чином, як і Ni, а саме:
визначаються саме таким чином, як і Ni, а саме: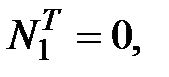


 . Отримані числові результати заносять до таблиці 2.3.
. Отримані числові результати заносять до таблиці 2.3. (2.16)
(2.16) (2.17)
(2.17)


 за формулою (2.16):
за формулою (2.16):
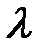 знаходиться P(
знаходиться P( ), згідно з таблицею 2.4, що дорівнює ймовірності того, що різниця D перевищить отримане значення.
), згідно з таблицею 2.4, що дорівнює ймовірності того, що різниця D перевищить отримане значення.
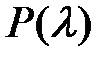
 1. Таким чином, закон нормального розподілу описує емпіричний з імовірністю 100 %.
1. Таким чином, закон нормального розподілу описує емпіричний з імовірністю 100 %. і
і  емпіричного розподілу визначаються за наступними формулами:
емпіричного розподілу визначаються за наступними формулами:

 (2.18)
(2.18)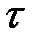 :
:
 (2.19)
(2.19) (2.20)
(2.20) складної машини, що складається з m деталей за умови, що ймовірність безвідмовної роботи всіх m елементів однакова, тобто виконується умова Pi(t)=P(t) для випадків, наведених на рис. 2.4 – 2.7.
складної машини, що складається з m деталей за умови, що ймовірність безвідмовної роботи всіх m елементів однакова, тобто виконується умова Pi(t)=P(t) для випадків, наведених на рис. 2.4 – 2.7. .
. =0,9.
=0,9. (2.21)
(2.21) (2.22)
(2.22)

 складної машини визначається за формулою:
складної машини визначається за формулою: (2.23)
(2.23)
 складної машини визначається за формулою:
складної машини визначається за формулою: (2.24)
(2.24)
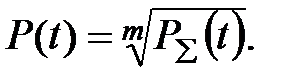 (2.25)
(2.25)
 (2.26)
(2.26)
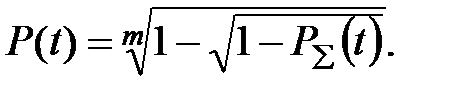 (2.27)
(2.27)
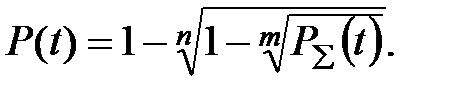 (2.28)
(2.28)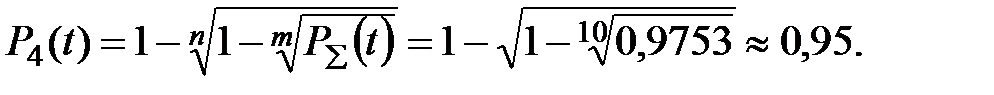
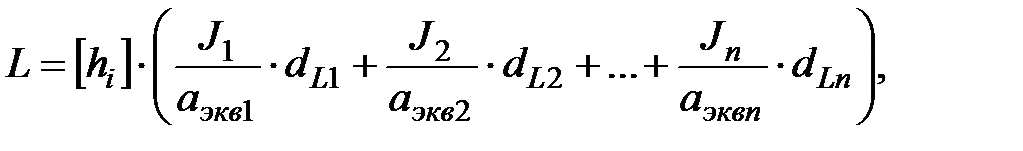 (2.29)
(2.29)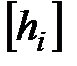 – допустима величина сумарного зносу накладок, мм;
– допустима величина сумарного зносу накладок, мм; (2.30)
(2.30) 1,
1,  2,
2,  3 – поправкові коефіцієнти, які знаходяться за результатами експериментальних спостережень;
3 – поправкові коефіцієнти, які знаходяться за результатами експериментальних спостережень;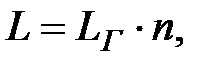 (2.31)
(2.31) 1,
1,  2,
2, 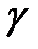 3 визначаються за залежностями:
3 визначаються за залежностями:

 (2.32)
(2.32) – відношення коефіцієнта при i -му режимі та базовому режимі;
– відношення коефіцієнта при i -му режимі та базовому режимі; у тисячах кілометрах пробігу.
у тисячах кілометрах пробігу. .
. , %
, %