
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача динамічного програмування знаходження найкоротшого шляхуСодержание книги
Поиск на нашем сайте
Динамічне програмування являє собою оптимизаційний метод, який орієнтований на розв’язання завдань, що виникають при виборі найкращої послідовності управлінських рішень. На відміну від більшості інших методів математичного програмування він не є різновидом симплексного методу. Динамічне програмування розроблене Беллманом і його колегами з “Рэнд Корпорейшн” і базується на принципі оптимальності Беллмана, що говорить: “ Оптимальна стратегія характеризується тією особливістю, що, яким би не був початковий стан системи й наслідку раніше прийнятих щодо неї рішень, всі подальші дії повинні становити оптимальну стратегію, що виходить зі стану системи, що явились результатом колишніх рішень*”. У цьому методі використана математична ідея рекурсії, суть якої найкраще пояснити за допомогою прикладу. Розглянемо завдання знаходження найкоротшого шляху на рисунку 8.1., де окружностями позначено міста, а лініями - дороги між ними. Довжина доріг (у кілометрах) зазначена цифрою над відповідними лініями. Мандрівник бажає потрапити з міста А в місто D найкоротшим з можливих шляхів, рухаючись у напрямку, який зазначено стрілками. Який оптимальний маршрут? Насамперед визначимо терміни, які будуть використані при розв’язанні завдання: стан, крок і стратегія. Стан - це конфігурація системи; у розглянутому прикладі під станом розуміється факт перебування мандрівника в даному місті. Крок - це перехід з одного стану в інший (суміжний з ним). У завданні визначення найкоротшого шляху під кроком розуміється переїзд із міста в місто, і будь-який маршрут, як видно з рисунку 1, містить у собі три кроки А→В, В→С и C→D.
Рис. 8.1. Завдання на знаходження найкоротшого шляху. Міста зображено кружками, а дороги між ними - лініями, цифри над лініями позначають довжину відповідної дороги.
Стратегія - це комплекс заходів, які спрямовані на досягнення поставленої мети. Так, вибір конкретного маршруту, наприклад A→B3→C2→D або A→B4→C1→D, являє собою стратегію розв’язання завдання знаходження найкоротшого шляху. Завдання динамічного програмування розв’язується у два етапи. На першому з них будується так зване рекуррентне співвідношення, що зв’язує між собою різні кроки, а на другому етапі на основі зазначеного співвідношення будується обчислювальна процедура**, мета якої - вибрати оптимальну стратегію. Для спрощення обчислювального процесу вводяться змінні кроку й стану. Нехай п число пророблених кроків, а і - конкретний стан на кожному кроці. Тоді (п, i) є стан і на кроці п. Завдання знаходження найкоротшого шляху, яке розглянуте із цих позицій, представлено на рисунку 8.2., де в окружностях зазначено відповідні змінні кроку й стану.
Рис 8.2. Завдання на знаходження найкоротшого шляху. У кружках, що зображують міста, зазначено відповідні змінні кроку й стану. Щоб побудувати рекуррентне співвідношення, визначимо f (n, i) як мінімальну дистанцію від міста (0,1), тобто А, до міста (п, i), a r (п-1, j: n, i) – як дистанцію від міста (п-1, j) до міста (п, i). Так, r (1,1:2,2) у розглянутому завданні становить 8 кілометрів. Відповідно до принципу оптимальності, будуємо рекуррентное співвідношення: f(n,i) = min | f (n -1,j) + r (п -1, j:n,i) |. де по визначенню f (0,1) = 0. Даний вираз є типовим для рекуррентного співвідношень, які досліджуються у динамічному програмуванні. Шляхом багаторазового використання даного виразу можна одержати наступне. * Існує більш лаконічне й чітке формулювання принципу оптимальності: стратегія оптимальних витрат для п кроків визначається економічними наслідками чергового розв’язку й стратегією оптимальних витрат для інших (п - 1) кроків. ** Таку обчислювальну процедуру прийнято називати реккурентним алгоритмом. Крок 1: f(1,1) = f (0, 1) + r (0,1:1,1) = 5; f(1,2) = f (0, 1) + r (0,1:1,2) = 6; f(1,3) = f (0, 1) + r (0,1:1,3) = 7; f(1,4) = f (0, 1) + r (0,1:1,4) = 6. Крок 2:
f(2,1) = min f (1,2) + r (1,2:2,1) = 6+6 = 12; f (1,3) + r (1,3:2,1) = 7+6 = 13; f (1,4) + r (1,4:2,1) = 6+7 = 13. Отже, f(2,1) = f (1, 1) + r (1,1:2,1) = 11. Аналогічно f(2,2) = f (1,3) + r (1,3:2,2) = 12. та f(2,3) = f (1,1) + r (1,1:2,3) = 10. Крок 3:
f(3,1) = min f (2,2) + r (2,2:3,1) = 12+2 = 14; f (2,3) + r (2,3:3,1) = 10+5 = 15. Отже, f(3,1) = f (2,2) + r (2,2:3,1) = 14. Мінімальна відстань від міста (0,1) до міста (3,1) дорівнює 14 кілометрам, а оптимальний маршрут визначається за допомогою зворотної підстановки, а саме f (3,1) = f (2,2) + r(2,2:3,1); = f (1,3) + r(1,3:2,2) + r(2,2:3,1); = f (0,1) + r(0,1:1,3) + r(1,3:2,2) + r(2,2:3,1). Оптимальною стратегією, таким чином, є маршрут: місто (0,1) →місто (1,3) → місто (2,2) →місто (3,1), тобто A→B3→C2→D.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.49.59 (0.009 с.) |


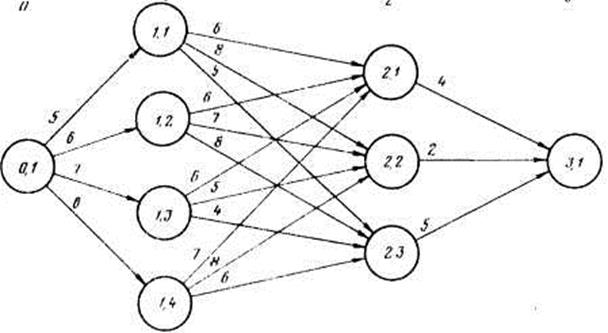
 f (1,1) + r (1,1:2,1) = 5+6 = 11;
f (1,1) + r (1,1:2,1) = 5+6 = 11; f (2,1) + r (2,1:3,1) = 11+4 = 15;
f (2,1) + r (2,1:3,1) = 11+4 = 15;


