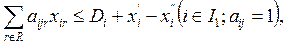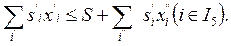Постановка економіко-математичної задачі.

Питання оперативного планування використання кормів, які заготовлені на стійловий період, представляють практичний інтерес. Оптимальний план повинен забезпечити найбільш раціональний розподіл запасів кормів між статево віковими групами і видами худоби з одночасним визначенням раціонів для кожної групи. При цьому необхідно знати, які корми слід докупити або продати (обміняти), а також скільки кормо-днів доцільно утримувати тварин для отримання максимальної кількості продукції тваринництва.

Бажаним критерієм оптимальності є максимум валової продукції тваринництва.

У відповідності з постановкою задачі в моделі будуть наступні групи змінних:

- види кормів і кормових добавок, з яких складають оптимальні раціони для груп худоби і птиці, які враховуються;

- кормо-дні перебування тварин у господарстві;

- корми, що купуються або продаються (обмінюються).

Перші дві групи змінних диференціюють за статево-віковими групами і видами худоби та птиці. Вони формують разом з обмеженнями по структурі кормових раціонів окремі блоки моделі. Таких блоків стільки, скільки груп і видів тварин враховується в задачі. Таким чином, модель оптимізації плану використання кормів має блочну структуру.

В моделі враховуються всі умови, які впливають на структуру використання кормів, що знаходить відображення в наступних групах обмежень:

- по поживним речовинам;

- відношенню окремих груп і видів кормів в існуючих групах;

- кормо-дням перебування окремих груп і видів худоби у господарстві;

- оптимальному розподілі (використанні) кожного виду корму з урахуванням можливої купівлі і (або) продажу;

- використанню коштів на купівлю недостатніх кормів.

Перші дві групи обмежень присутні в кожному блоці, і з їх допомогою визначаються оптимальні норми годівлі відповідної групи або виду худоби. Три останні групи є обмеженнями з'єднувального блоку і забезпечують пов’язання всіх умов у моделі.

Для запису вказаних груп умов повинні бути відомі наступні техніко-економічні коефіцієнти і константи:

- вміст поживних речовин в 1 кг кормів і добавок;

- потреба в поживних речовинах у розрахунку на 1 кормо-день кожної групи або виду худоби;

- допустимі межі (інтервали) потреби в корм.од. по групам кормів для кожної групи або виду худоби;

- допустимі межі (інтервали) утримання окремих груп або видів худоби в господарстві у кормо-днях;

- кошти, які виділяються на закупівлю недостатніх кормів;

- ціни на всі види кормів, що купуються або продаються.

Коефіцієнтами цільової функції є показники вартості продукції в розрахунку на 1 кормо-день за всіма групами і видами худоби, які враховуються.

Вихідна інформація для побудування числової моделі.

Необхідно розробити оптимальний план використання заготовлених у господарстві кормів. Критерій оптимальності – максимум валової продукції тваринництва. В господарстві утримують два види худоби – молочне стадо корів і свині на відгодівлі. Молочне стадо необхідно утримувати не менше 400 тис. кормо-днів, а свиней – не менше 150 тис. і не більше 250 тис. кормо-днів.

Добовий раціон корови живою масою 420 кг з надоєм 11 кг молока жирністю 3,8 % повинен містити: к.од. – не менше 9,5, перетравного протеїну – не менше 1005 г. За рахунок концентратів у раціоні повинно бути не менше 2 і не більше 3,5 к.од., грубих – від 2 до 4, силосу – не менше 4 к.од. Вартість продукції в розрахунку на 1 кормо-день корови становить 3,85 грн. (11*0,35 – закупівельна ціна 1 кг молока).

На кожний кормо-день свиней на відгодівлі витрачається 2,5 кг к.од. і 272 г ПП, причому за рахунок концентратів – не менше 1,8 і коренеплодів – не менше 0,7 к.од. Вартість продукції на 1 кормо-день свиней становить 0,9 грн. (0,45*2, де перше число означає приріст живої маси на 1 голову свиней, кг, друге – закупівельну ціну 1 кг).

Види заготовлених кормів, їх кількість і вміст поживних речовин у них подані в таблиці 4.

6. Інформація по заготовленим у господарстві кормам

Корми	Кількість, т	Міститься в 1 кг
к.од.	ПП, г
Зерно фуражне Комбікорм Сіно Силос Коренеплоди		1,2 1,1 0,5 0,15 0,12

 

Господарство може додатково придбати комбікорм по 14 грн. за 1 ц і реалізувати надлишок сіна, якщо такий буде, по 50 грн. за 1 т. На придбання кормів виділено 50 тис. грн.

Розробка числової моделі.

У відповідності з умовами задачі введемо змінні величини:

x₁ – зернофуражне на корм коровам, кг;

x₂ – комбікорм для корів, кг;

x₃ – сіно для корів, кг;

x₄ – силос для корів, кг;

x₅ – кормо-дні корів;

x₆ – зерно фуражне на корм свиням, кг;

x₇ – комбікорм для свиней, кг;

x₈ – коренеплоди для свиней, кг;

x₉ – кормо-дні свиней на відгодівлі;

x₁₀ – комбікорм, що купують, ц;

x₁₁ – надлишок сіна, що реалізується, т.

Модель буде складатися з двох блоків, перший з яких призначений для оптимізації кормового раціону корів, а другий – свиней.

Основні обмеження служать для запису умов по балансам поживних речовин. Так, в першому блоці обмеження по к.од. для корів матиме вигляд:

1. 1,2x₁+1,1x₂+0,5x₃+0,15x₄>=9,5x₅,

де техніко-економічні коефіцієнти при перемінних з x₁ до x₄ відображають вміст к.од. в 1 кг відповідних кормів для корів, а коефіцієнт при перемінній x₅ відображає потребу в к.од. в розрахунку на 1 кормо-день корови. Зміст цього обмеження полягає в тому, що загальний вихід к.од. від усіх кормів, які згодовуються корові, повинен бути не менше 9,5 в розрахунку на кожний кормо-день, а кількість кормо-днів є величиною перемінною і визначається в результаті розв’язання задачі на ЕОМ.

Якщо перенести в ліву частину нерівності 9,5x_5, отримаємо

-1,2x₁-1,1x₂-0,5x₃-0,15x₄+9,5x₅<=0.

2. Аналогічно записують по перетравному протеїну для корів:

-110x₁-125x₂-48x₃-14x₄+1005x₅<=0.

Математичний запис обмежень по поживним речовинам матиме вигляд

або після перетворення

де і – номер (або індекс) обмежень;

І₁ – множина, яка включає номера обмежень по поживним речовинам;

j – номер перемінної;

А – множина, яка включає номера перемінних, які позначають види кормів;

R - множина, яка включає номера перемінних, які позначають види і групи тварин (в кормо-днях);

r – номер перемінної, яка позначає види і групи тварин;

x_jr – перемінна, яка позначає шукану кількість корму j-того виду, який йде на корм r-й групі худоби;

x_r – перемінна, яка показує кількість кормо-днів перебування у господарстві r-ї групи тварин;

u_ijr – техніко-економічний коефіцієнт, який показує вміст і-тої поживної речовини в одиниці j-того виду корму, який згодовується r-тому виду або групі тварин;

a_ir – техніко-економічний коефіцієнт, який означає потребу в і-тій поживній речовині в розрахунку на 1 кормо-день r-тої групи або виду худоби.

3. З допомогою другої групи обмежень записують умови по окремим групам кормів для корів. Так, третє обмеження – “концентратів для корів не менше” – має вигляд:

1,2x₁+1,1x₂>=2x₅, або -1,2x₁-1,1x₂+2x₅<=0.

4. Умову – “концентратів для корів не більше” можна записати так:

1,2x₁+1,1x₂<=3,5x₅, або 1,2x₁+1,1x₂-3,5x₅<=0.

5. Так само записують умови по грубим кормам:

0,5x₃+2x₅<=0.

6. 0,5x₃-4x₅<=0.

7. Останнє обмеження в першому блоці - по силосу:

0,15x₄>=4x₅ або -0,15x₃+4x₅<=0.

Техніко-економічні коефіцієнти при перемінній x₅ позначають межі вмісту кормових одиниць у відповідних групах кормів в розрахунку на 1 кормо-день.

Математично записати умови по к.од. для окремих груп кормів можна наступним чином:

де І₂ – множина, яка включає номера обмежень по кормовим одиницям для окремих груп кормів.

Таким чином, перший блок моделі включає 5 перемінних і 7 обмежень.

Аналогічно записують обмеження другого блоку, в якому визначають оптимальний раціон свиней на відгодівлі. Цей блок включає 4 перемінних (з x₆ до x₉) і 4 обмеження (з 8-го до 11-го).

8. Обмеження по к.од. для свиней має вигляд:

-1,2x₆-1,1x₇-0,12x₈+2,5x₉<=0.

9. Обмеження по перетравному протеїну для свиней записується так:

-110x₆-125x₇-9x₈+272x₉<=0.

10. Запишемо обмеження по концентратам і коренеплодам для свиней:

-1,2x₆-1,1x₇+1,8x₉<=0.

11. -0,12x₈+0,7x₉<=0.

12. В умовах з’єднувального блоку є обмеження по кількості кормо-днів перебування корів і свиней в господарстві.

Дванадцяте обмеження має вигляд: x₅>=400000.

13. x₉>=150000.

14. x₉<=250000.

Математичний запис умов по числу кормо-днів перебування тварин у господарстві має вигляд:

^.

де І₃ – множина, яка включає номера обмежень по кормо-дням перебування тварин у господарстві;

B’_ír і B”_ir – константи, які позначають нижні та верхні межі перебування r-ї групи або виду худоби у господарстві.

Наступна група умов з’єднувального блоку відноситься до розподілу наявних запасів кормів між включеними у модель групами і видами худоби з урахуванням можливої купівлі недостатніх і реалізації надлишкових.

15. Обмеження по розподілу фуражного зерна:

x₁+x₆<=300000.

де перемінні позначають об’єм згодованого фуражного зерна відповідно коровам і свиням, а константа 300000 показує його запас у господарстві (кг).

16. Наступне обмеження відображає використання (розподіл) комбікорму з урахуванням можливої його купівлі:

x₂+x₇<=1000000+100x_10, або x₂+x₇-100x₁₀<=1000000,

де 100x₁₀ означає можливе збільшення наявного запасу комбікорму понад 1000 т.

17. Використання сіна з урахуванням його можливого продажу:

x₃<=3600000-1000x_11, або x₃+1000x₁₁<=3600000.

де 1000x₁₁ - об’єм запланованого до продажу сіна в тонах, знак “-“ показує. Що наявний в господарстві запас сіна при цьому зменшиться.

В наступних двох обмеженнях (18 і 19) відображене використання силосу і коренеплодів:

18. x₄<=12000000.

19. x₃<=1300000.

Математичний запис умов по використанню (розподілу) окремих видів кормів має вигляд:

або

де І₄ – множина, яка включає номера обмежень по розподілу кормів;

Dj – константа, яка означає запас j-того корму в господарстві;

x’j – перемінна, яка показує розмір купівлі j-того корму;

x”j – перемінна, яка визначає розмір продажу надлишку j-того виду корму.

Останнє обмеження, яке відноситься до умов з’єднувального блоку, визначає використання матеріально-грошових засобів на придбання кормів з урахуванням засобів, отриманих від продажу їх надлишків:

20. 14x₁₀<=50000+50x_11, або 14x₁₀-50x₁₁<=50000,

де коефіцієнти при перемінних x₁₀ і x₁₁ показують відповідно ціни купівлі 1 ц комбікорму і продажу 1 т надлишків сіна. Константа 50000 позначає розмір коштів, які господарство виділяє на придбання кормів, який може зрости на величину засобів, отриманих від реалізації надлишків сіна, тобто на 50x_11.

Математичний запис цієї групи умов має вигляд:

де І₅ – множина, яка включає номера обмежень по використанню матеріально-грошових засобів на купівлю кормів;

S – константа, яка вказує розмір виділених коштів;

s’i та s”i – техніко-економічні коефіцієнти, які позначають ціни придбання і реалізації кормів за одиницю.

Критерієм оптимальності в даній задачі є максимум виходу продукції тваринництва в грошовому виразі. Цільова функція має вид:

3,85x₅+0,9x₉ Þ max,

де 5,5 і 2,25 – коефіцієнти цільової функції при перемінних, які позначають кормо-дні перебування корів і свиней у господарстві, які показують вартість валової продукції на 1 кормо-день корів і свиней на відгодівлі.

Математичний запис цільової функції має вид:

де Cr – коефіцієнт цільової функції, який відображає вартість продукції в розрахунку на 1 кормо-день r-ї групи або виду тварин.

Результати розв’язання задачі подані в таблиці 5.

Як бачимо, господарство в змозі утримувати більше великої рогатої худоби, ніж було задано умовами. По оптимальному рішенню тривалість утримання корів повинна зрости до 450 тис. або на 50 тис. кормо-днів. Кормо-дні перебування свиней за оптимальним варіантом склали 222857. цей показник знаходиться в межах мінімуму і максимуму. В оптимальному варіанті корми повністю використовуються. Необхідна додаткова закупівля комбікорму в кількості 18,9 т, на що необхідно витрати 2,65 тис. грн. з 50 тис., які виділені на придбання недостатніх кормів.

Вартість продукції тваринництва за оптимальним планом 1933,1 тис. грн.

В результаті розв’язання задачі на ЕОМ поряд з оптимальним використанням і розподілом кормів по видам худоби отримали також оптимальні норми витрат кормів для корів і свиней.

Двоїста оцінка 18-го обмеження (по розподілу силосу) – 0,144. Це значить, що при збільшенні об’єму цього корму на 1 кг вартість валової продукції збільшиться на величину двоїстої оцінки, тобто на 14,4 коп. Ця оцінка пов’язана з оцінкою 7-го обмеження, яка дорівнює 0,96, - використання кожної додаткової кормової одиниці силосу збільшить функціонал на 96 коп. Дійсно, 1 кг силосу містить 0,15 к.од. (0,96/0,144).

5. Оптимальний розподіл кормів

Показники	Корови	Свині	Всього
Кормо-дні перебування у господарстві: за умовами за результатами оптимального розв’язання на ЕОМ Розподіл кормів, т: зерно комбікорм сіно силос кормові коренеплоди Вартість продукції тваринництва, тис. грн.	Не менше 400000     627,6 - 1732,5	150000 – 250000     - 391,3 - - 200,6	-   1018,9 1933,1