Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка моделей с распределенными лагамиСодержание книги
Поиск на нашем сайте
Методы оценки моделей с распределенными лагами в независимых переменных во многом определяются тем, конечное или бесконечное число лагов содержит соответствующее регрессионное уравнение. Модель, описываемая уравнением
с конечным числом лагов k (максимальный лаг определяет порядок модели), оценивается достаточно просто путем сведения ее к уравнению множественной регрессии. В этом случае, полагая в (6.13) Х 0 = хt, Х 1 = хt 1, …, Хk = хt k, получают уравнение:
оценка параметров которого может быть произведена по МНК. Возможные трудности при оценивании подобных моделей могут быть связаны с проявлением мультиколлинеарности или автокорреляции. В модели с бесконечным числом лагов, теоретическое уравнение которой имеет вид:
предполагается, что влияние переменной Х не заканчивается в момент времени k, а продолжается бесконечно, убывая по определенному закону. Подобные модели встречаются на практике и имеют достаточно ясный экономический смысл, так как логично предположить, что влияние прошлых значений объясняющих переменных на текущее значение зависимой переменной будет тем меньше, чем дальше по времени наблюдались эти показатели. Отметим, что в моделях (6.14) и (6.15) коэффициент b 0 называют краткосрочным мультипликатором в силу того, что он характеризует изменение среднего значения переменной Y под воздействием единичного изменения переменной Х в тот же самый период времени. Для модели с бесконечным числом лагов можно применить распределение Койка, в котором принимается, что коэффициенты (или «веса») bk при лагированных переменных убывают с каждым шагом по времени в геометрической прогрессии [33]: bk = b 0 k, k = 0, 1, 2, …, (6.16) где параметр (0 < < 1) характеризует скорость убывания коэффициентов с увеличением лага. Тогда модель (6.15) преобразуется в уравнение:
Модель (6.17) содержит теперь только три параметра (, b 0,), однако ее оценивание затруднено тем, что она является нелинейной. Наиболее часто для определения параметров уравнения (6.17) используется процедура, которая называется нелинейным методом наименьших квадратов. Эта процедура реализуется в большинстве компьютерных эконометрических пакетов. Сущность метода заключается в следующем. 1. С достаточно мелким фиксированным шагом (например, 0,01 или 0,001) перебираются все значения из интервала (0, 1). 2. Для каждого значения рассчитывается величина:
Значение р (предел суммирования) определяется из условия, что дальнейшие члены ряда вносят в его сумму незначительный вклад. 3. Для каждого z по МНК оценивается уравнение:
4. Выбирается то уравнение (6.19), которое обеспечивает наибольший коэффициент детерминации R 2. Соответствующее значение Другой способ оценивания состоит в преобразовании уравнения (6.17) в авторегрессионное уравнение. Для этого из уравнения (6.17) вычитается то же самое уравнение, сдвинутое по времени на один шаг назад и умноженное на. В результате получим следующее выражение:
или
Здесь vt = t t 1 (t = 1, …, n) представляет собой скользящую среднюю между t и t 1. Проведенное преобразование позволило избавиться от бесконечного числа лаговых переменных. С помощью МНК мы можем оценить параметры полученной двухфакторной регрессионной модели. При оценивании уравнения (6.20) следует учитывать возможное проявление автокорреляции для случайных отклонений vt, а также появление в модели, в качестве регрессора, переменной уt 1, которая, в принципе, носит случайный (стохастический) характер. Поэтому оценки параметров, и b 0 могут обладать недостатками, связанными с нарушением условий классической регрессионной модели. В модели геометрических лагов Койка на коэффициенты регрессии накладываются достаточно сильные ограничения, которые в ряде случаев могут не выполняться. Так, например, встречаются ситуации, когда значения лаговой объясняющей переменной за 3–4 периода от момента наблюдения оказывают на зависимую переменную большее влияние, чем текущее или предшествующее ему значение регрессора (b 3, b 4 > b 0, b). В таких случаях следует применять модели полиномиальных лагов Алмон, которые достаточно гибко отражают изменения в поведении лаговых объясняющих переменных [28]. В основе модели Алмон лежит предположение, что «веса» коэффициентов bi в уравнении (6.13) аппроксимируются полиномами определенной степени от величины лага i:
Для простоты изложения метода Алмон будем считать, что bi определяется квадратичной зависимостью:
Тогда уравнение (6.13) после подстановки (6.22) может быть представлено в виде:
Полагая, что
параметры которого, с 0, с 1 и с 2 могут быть оценены по МНК. Затем коэффициенты bi определяются из соотношения (6.22). В общем случае модель полиномиальных лагов Алмон содержит только r + 2 неизвестных параметров, где r степень полинома. Для эффективного применения метода Алмон рекомендуется вначале определиться с количеством лагов k и подобрать степень полинома r, описывающего структуру лага. Проверка адекватности модели может быть проведена на основе обычной F -статистики (см. раздел 3.3.2).
Авторегрессионные модели
Рассмотрим два примера авторегрессионных динамических моделей, наиболее часто встречающихся в экономике: модель адаптивных ожиданий и модель частичной корректировки. Как будет показано далее, эти модели можно также отнести к семейству моделей Койка. В уравнение модели адаптивных ожиданий в качестве объясняющей переменной вместо текущего значения xt входит ожидаемое (долгосрочное) значение
Так как ожидаемые значения не являются фактически наблюдаемыми, предполагается, что они связаны следующим соотношением:
согласно которому ожидания постоянно пересматриваются (корректируются) в определенной пропорции от разности между наблюдаемым xt и ожидаемым Уравнение (6.26) можно переписать в виде:
из которого следует, что значение переменной Подставляя (6.27) в уравнение (6.25), получим:
Из уравнения (6.28) может быть исключено ненаблюдаемое значение объясняющей переменной
Далее, выражая
где Можно заметить, что уравнение (6.30) по форме аналогично уравнению (6.20), полученному в результате преобразования Койка. На основании этого можно предположить, что процесс адаптивных ожиданий, описываемый уравнениями (6.25) и (6.27), может быть рассмотрен в рамках модели геометрических лагов Койка. В самом деле, воспользовавшись уравнением (6.27) для ожидаемого значения
Подставляя (6.31) в (6.27), получим:
Продолжая процедуру использования уравнения (6.27) для значения
Подставляя полученное для
Заметим, что полученное уравнение (6.33) совпадает с моделью геометрических лагов Койка и его параметры можно оценить, например, с помощью нелинейного метода наименьших квадратов. Модель адаптивных ожиданий может быть использована при анализе зависимости объема производства от ожидаемой цены на производимую продукцию, инвестиций от процентной ставки, цены на товар от ожидаемых цен на сырье или комплектующие изделия и в других ситуациях, где экономические показатели оказываются зависимыми от ожидаемых значений факторов. В модели частичной корректировки предполагается, что желаемое (оптимальное, целевое) значение исследуемой переменной Y определяется регрессионным уравнением [11,28]:
Так как ожидаемое значение
согласно которому фактическое приращение зависимой переменной пропорционально разнице между ее желаемым значением и значением в предыдущий период. С другой стороны, выражение (6.35) показывает, что наблюдаемое значение переменной Y не выходит мгновенно на желаемое значение, а изменяется только на долю в нужном направлении. Здесь (0 1) коэффициент корректировки. Уравнение (6.35) можно представить в следующем виде:
т. е. текущее значение Подставляя (6.34) в (6.36), получим следующее регрессионное уравнение:
которое и называется моделью частичной корректировки. Из уравнений (6.35) и (6.36) следует, что чем больше, тем быстрее идет корректировка; при = 1 полная корректировка происходит за один период, при = 0 корректировка не происходит вовсе. Например, если = 0,5, то экономический агент предполагает в каждом периоде сокращать разрыв между текущим и желаемым значениями переменной Y наполовину. Следует заметить, что модель частичной корректировки также относится к авторегрессионным моделям, поскольку включает в себя случайную объясняющую переменную Модели частичной корректировки применяются для оценки ожидаемых (желаемых) значений экономических показателей в зависимости от действующих на них текущих значений факторов (желаемого размера запасов от уровня продаж, желаемого запаса капитала от объема выпуска и др.). Необходимо отметить, что достаточно часто регрессоры в динамических моделях носят случайный (стохастический) характер. Например, авторегрессионные модели следует рассматривать как модели со стохастическими регрессорами. Во многих случаях это приводит к наличию корреляции между регрессорами и случайными отклонениями регрессионной модели, что, в свою очередь, делает МНК-оценки смещенными и несостоятельными. Одним из наиболее распространенных приемов устранения влияния указанной корреляции является метод инструментальных переменных. Идея метода заключается в том, чтобы переменную
коррелирующую с t, заменить новой, так называемой инструментальной переменной, которая бы достаточно тесно коррелировала с Оценивание с помощью инструментальных переменных обычно тесно связано с процедурой, которая называется двухшаговым методом наименьших квадратов (ДМНК). На первом этапе осуществляется регрессия исходных переменных Xj на Z: Xj = Z + v со случайным отклонением v и определяются оценки (прогнозные значения) Чтобы избежать возможных неверных выводов по модели, авторегрессионное уравнение (6.11) необходимо проверить на наличие автокорреляции остатков. Как уже было отмечено ранее (см. раздел 5.3.1), тест Дарбина-Уотсона (DW) в данном случае неприменим, так как не выполняются условия, лежащие в его обосновании. При наличии в правой части авторегрессионного уравнения лагированных зависимых переменных значения статистики Дарбина-Уотсона будут смещены в сторону принятия гипотезы об отсутствии автокорреляции, когда на самом деле эта гипотеза неверна. Для выявления автокорреляции первого порядка в авторегрессионных моделях может быть использован h-тест Дарбина [1]. Например, для уравнения (6.11) наблюдаемое значение h- статистики рассчитывается по формуле:
где n объем выборки; Если верна нулевая гипотеза H 0 об отсутствии автокорреляции первого порядка остатков модели, то, при достаточно большом объеме выборки, h -статистика имеет стандартное нормальное распределение. Например, гипотеза H 0 отвергается при уровне значимости = 0,05 в пользу присутствия положительной автокорреляции, если h > 1,645. При обнаружении автокорреляции в авторегрессионных моделях для ее устранения наиболее часто используются такие способы, как авторегрессионное преобразование и преобразование методом скользящих средних.
Вопросы и упражнения для самопроверки
1. Что понимается под временным рядом и динамической моделью? 2. Охарактеризуйте общую структуру временного ряда. 3. Каковы принципы построения моделей тренда? 4. Сформулируйте понятие стационарного временного ряда. 5. Опишите схему применения метода скользящих средних для выравнивания (сглаживания) временного ряда. 6. В чем заключаются аналитические методы выравнивания временного ряда? 7. В чем суть коэффициента автокорреляции и частного коэффициента автокорреляции временного ряда? 8. Как определить наличие сезонной составляющей в структуре временного ряда с помощью автокорреляционной функции? 9. Сформулируйте общие принципы прогнозирования экономических показателей на основе временных рядов. 10. В таблице приведены поквартальные данные о прибыли предприятия (млн. руб.)
а) Для данного временного ряда рассчитайте коэффициенты автокорреляции уровней ряда первого и второго порядка; б) Проведите выравнивание (сглаживание) временного ряда в) Постройте аналитическую функцию для моделирования основной тенденции временного ряда, полагая тренд линейным. 11. В чем состоит различие между моделями с распределенными лагами и авторегрессионными моделями? 12. Опишите процедуру оценивания моделей с распределенными лагами на основе распределения (преобразования) Койка. 13. Опишите общую схему применения метода Алмон. 14. Сформулируйте, в чем заключается суть нелинейного метода наименьших квадратов? 15. Как определяется автокорреляция остатков в авторегрессионных моделях? 16. Опишите основные свойства модели адаптивных ожиданий. 17. В чем состоит отличие модели адаптивных ожиданий от модели частичной корректировки? 18. В чем суть метода инструментальных переменных? 19. Приведите общую схему оценивания на основе двухшагового метода наименьших квадратов (ДМНК). 20. По данным за 30 месяцев некоторого временного ряда Охарактеризуйте структуру ряда; составьте наиболее обоснованное уравнение авторегрессии.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.20.205 (0.011 с.) |

 (6.13)
(6.13) (6.14)
(6.14) (6.15)
(6.15) (6.17)
(6.17) (6.18)
(6.18) (6.19)
(6.19) принимается за оценку параметра. Найденные оценки, b 0 и подставляются в (6.17).
принимается за оценку параметра. Найденные оценки, b 0 и подставляются в (6.17).
 (6.20)
(6.20) (6.21)
(6.21) . (6.22)
. (6.22)
 . (6.23)
. (6.23)

 получим уравнение:
получим уравнение: (6.24)
(6.24) , т. е. исследуемая величина Y зависит от ожидаемого значения фактора-аргумента:
, т. е. исследуемая величина Y зависит от ожидаемого значения фактора-аргумента: (6.25)
(6.25)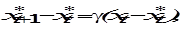 (6.26)
(6.26) значениями переменной Х в предыдущем периоде. Коэффициент 0 1 называется коэффициентом ожидания (адаптации). Если = 0, то ожидания являются неизменными (статичными):
значениями переменной Х в предыдущем периоде. Коэффициент 0 1 называется коэффициентом ожидания (адаптации). Если = 0, то ожидания являются неизменными (статичными):  Если же = 1, то
Если же = 1, то  что означает мгновенно реализуемые ожидания.
что означает мгновенно реализуемые ожидания. (6.27)
(6.27)
 . (6.28)
. (6.28) (6.29)
(6.29) (6.30)
(6.30) .
. . (6.31)
. (6.31) .
.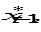 затем для
затем для  и так до бесконечности (итерируя (6.27)), получим соотношение:
и так до бесконечности (итерируя (6.27)), получим соотношение: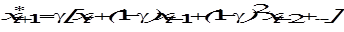 . (6.32)
. (6.32)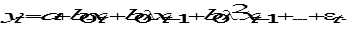 (6.33)
(6.33)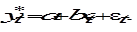 (6.34)
(6.34) не является фактически существующим, то относительно его выдвигается условие частичной корректировки:
не является фактически существующим, то относительно его выдвигается условие частичной корректировки: (6.35)
(6.35)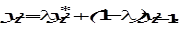 (6.36)
(6.36) равно взвешенному среднему ожидаемого уровня и фактического значения зависимой переменной в предыдущем периоде.
равно взвешенному среднему ожидаемого уровня и фактического значения зависимой переменной в предыдущем периоде. (6.37)
(6.37)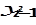 и может быть сведена к модели Койка. Однако для данной модели переменная
и может быть сведена к модели Койка. Однако для данной модели переменная 
 . Их мы теперь будем считать новыми независимыми переменными, и на втором этапе оценка вектора параметров В строится с помощью обычной регрессии Y на
. Их мы теперь будем считать новыми независимыми переменными, и на втором этапе оценка вектора параметров В строится с помощью обычной регрессии Y на 

 (6.38)
(6.38) дисперсия оценки коэффициента при
дисперсия оценки коэффициента при  оценка коэффициента автокорреляции первого порядка, которую можно вычислить по формуле (5.23):
оценка коэффициента автокорреляции первого порядка, которую можно вычислить по формуле (5.23):