
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временные ряды и их характеристикиСодержание книги
Поиск на нашем сайте
Динамические модели
Большинство динамических моделей можно разделить на два вида: модели с распределенными лагами и авторегрессионные модели. Лагированные модели встречаются каждый раз, когда зависимая переменная yt с некоторым запаздыванием (лагом) реагирует на изменение действующих на экономический объект факторов. Например, объем выпуска продукции некоторым предприятием в год t обычно зависит не только от инвестиций It в этот год, но и от инвестиций в предыдущие годы:
где е – случайная составляющая (ошибка) модели. Уравнение (6.10) является примером модели с распределенными лагами. Авторегрессионная модель включает в себя в качестве регрессора лагированные значения зависимой переменной Y и, например, может быть представлена следующим регрессионным уравнением:
В простейшем случае уравнение
описывает авторегрессионный процесс первого порядка, в котором исследуемая величина yt определяется ее значениями в предшествующий период. Подобная модель для случайных отклонений регрессии (= 0) была рассмотрена нами в предыдущей главе (раздел 5.3.2). Основой для построения авторегрессионных моделей может служить экономическая ситуация, когда под воздействием объясняющих переменных формируется не сама величина Y, а ее желаемое (ожидаемое) значение, которое в результате проявления определенных причин может отклоняться от фактического значения yt [4,11,28]. В данном случае в уравнение модели в качестве регрессора должно входить желаемое (долгосрочное) значение величины Y с соответствующим корректирующим коэффициентом. Подобные модели получили название моделей частичной корректировки. Например, соответствующая модель выплаты дивидендов некоторой фирмой в момент времени t подробно рассмотрена Дж. Линтнером [22]. В моделях адаптивных ожиданий происходит постоянная корректировка ожидаемого уровня результата на основе получаемой информации о реальных значениях исследуемого экономического показателя. Если реальное значение показателя оказалось больше ожидаемого, то ожидаемое в следующем периоде значение корректируется в сторону увеличения. В противном случае – наоборот. При этом величина корректировки должна быть пропорциональна разности между реальным и ожидаемым значениями. Наиболее известными из экономической теории примерами моделей адаптивных ожиданий являются модель потребления М. Фридмена и модель гиперинфляции Ф. Кейгена [22].
Авторегрессионные модели
Рассмотрим два примера авторегрессионных динамических моделей, наиболее часто встречающихся в экономике: модель адаптивных ожиданий и модель частичной корректировки. Как будет показано далее, эти модели можно также отнести к семейству моделей Койка. В уравнение модели адаптивных ожиданий в качестве объясняющей переменной вместо текущего значения xt входит ожидаемое (долгосрочное) значение
Так как ожидаемые значения не являются фактически наблюдаемыми, предполагается, что они связаны следующим соотношением:
согласно которому ожидания постоянно пересматриваются (корректируются) в определенной пропорции от разности между наблюдаемым xt и ожидаемым Уравнение (6.26) можно переписать в виде:
из которого следует, что значение переменной Подставляя (6.27) в уравнение (6.25), получим:
Из уравнения (6.28) может быть исключено ненаблюдаемое значение объясняющей переменной
Далее, выражая
где Можно заметить, что уравнение (6.30) по форме аналогично уравнению (6.20), полученному в результате преобразования Койка. На основании этого можно предположить, что процесс адаптивных ожиданий, описываемый уравнениями (6.25) и (6.27), может быть рассмотрен в рамках модели геометрических лагов Койка. В самом деле, воспользовавшись уравнением (6.27) для ожидаемого значения
Подставляя (6.31) в (6.27), получим:
Продолжая процедуру использования уравнения (6.27) для значения
Подставляя полученное для
Заметим, что полученное уравнение (6.33) совпадает с моделью геометрических лагов Койка и его параметры можно оценить, например, с помощью нелинейного метода наименьших квадратов. Модель адаптивных ожиданий может быть использована при анализе зависимости объема производства от ожидаемой цены на производимую продукцию, инвестиций от процентной ставки, цены на товар от ожидаемых цен на сырье или комплектующие изделия и в других ситуациях, где экономические показатели оказываются зависимыми от ожидаемых значений факторов. В модели частичной корректировки предполагается, что желаемое (оптимальное, целевое) значение исследуемой переменной Y определяется регрессионным уравнением [11,28]:
Так как ожидаемое значение
согласно которому фактическое приращение зависимой переменной пропорционально разнице между ее желаемым значением и значением в предыдущий период. С другой стороны, выражение (6.35) показывает, что наблюдаемое значение переменной Y не выходит мгновенно на желаемое значение, а изменяется только на долю в нужном направлении. Здесь (0 1) коэффициент корректировки. Уравнение (6.35) можно представить в следующем виде:
т. е. текущее значение Подставляя (6.34) в (6.36), получим следующее регрессионное уравнение:
которое и называется моделью частичной корректировки. Из уравнений (6.35) и (6.36) следует, что чем больше, тем быстрее идет корректировка; при = 1 полная корректировка происходит за один период, при = 0 корректировка не происходит вовсе. Например, если = 0,5, то экономический агент предполагает в каждом периоде сокращать разрыв между текущим и желаемым значениями переменной Y наполовину. Следует заметить, что модель частичной корректировки также относится к авторегрессионным моделям, поскольку включает в себя случайную объясняющую переменную Модели частичной корректировки применяются для оценки ожидаемых (желаемых) значений экономических показателей в зависимости от действующих на них текущих значений факторов (желаемого размера запасов от уровня продаж, желаемого запаса капитала от объема выпуска и др.). Необходимо отметить, что достаточно часто регрессоры в динамических моделях носят случайный (стохастический) характер. Например, авторегрессионные модели следует рассматривать как модели со стохастическими регрессорами. Во многих случаях это приводит к наличию корреляции между регрессорами и случайными отклонениями регрессионной модели, что, в свою очередь, делает МНК-оценки смещенными и несостоятельными. Одним из наиболее распространенных приемов устранения влияния указанной корреляции является метод инструментальных переменных. Идея метода заключается в том, чтобы переменную
коррелирующую с t, заменить новой, так называемой инструментальной переменной, которая бы достаточно тесно коррелировала с Оценивание с помощью инструментальных переменных обычно тесно связано с процедурой, которая называется двухшаговым методом наименьших квадратов (ДМНК). На первом этапе осуществляется регрессия исходных переменных Xj на Z: Xj = Z + v со случайным отклонением v и определяются оценки (прогнозные значения) Чтобы избежать возможных неверных выводов по модели, авторегрессионное уравнение (6.11) необходимо проверить на наличие автокорреляции остатков. Как уже было отмечено ранее (см. раздел 5.3.1), тест Дарбина-Уотсона (DW) в данном случае неприменим, так как не выполняются условия, лежащие в его обосновании. При наличии в правой части авторегрессионного уравнения лагированных зависимых переменных значения статистики Дарбина-Уотсона будут смещены в сторону принятия гипотезы об отсутствии автокорреляции, когда на самом деле эта гипотеза неверна. Для выявления автокорреляции первого порядка в авторегрессионных моделях может быть использован h-тест Дарбина [1]. Например, для уравнения (6.11) наблюдаемое значение h- статистики рассчитывается по формуле:
где n объем выборки; Если верна нулевая гипотеза H 0 об отсутствии автокорреляции первого порядка остатков модели, то, при достаточно большом объеме выборки, h -статистика имеет стандартное нормальное распределение. Например, гипотеза H 0 отвергается при уровне значимости = 0,05 в пользу присутствия положительной автокорреляции, если h > 1,645. При обнаружении автокорреляции в авторегрессионных моделях для ее устранения наиболее часто используются такие способы, как авторегрессионное преобразование и преобразование методом скользящих средних.
Вопросы и упражнения для самопроверки
1. Что понимается под временным рядом и динамической моделью? 2. Охарактеризуйте общую структуру временного ряда. 3. Каковы принципы построения моделей тренда? 4. Сформулируйте понятие стационарного временного ряда. 5. Опишите схему применения метода скользящих средних для выравнивания (сглаживания) временного ряда. 6. В чем заключаются аналитические методы выравнивания временного ряда? 7. В чем суть коэффициента автокорреляции и частного коэффициента автокорреляции временного ряда? 8. Как определить наличие сезонной составляющей в структуре временного ряда с помощью автокорреляционной функции? 9. Сформулируйте общие принципы прогнозирования экономических показателей на основе временных рядов. 10. В таблице приведены поквартальные данные о прибыли предприятия (млн. руб.)
а) Для данного временного ряда рассчитайте коэффициенты автокорреляции уровней ряда первого и второго порядка; б) Проведите выравнивание (сглаживание) временного ряда в) Постройте аналитическую функцию для моделирования основной тенденции временного ряда, полагая тренд линейным. 11. В чем состоит различие между моделями с распределенными лагами и авторегрессионными моделями? 12. Опишите процедуру оценивания моделей с распределенными лагами на основе распределения (преобразования) Койка. 13. Опишите общую схему применения метода Алмон. 14. Сформулируйте, в чем заключается суть нелинейного метода наименьших квадратов? 15. Как определяется автокорреляция остатков в авторегрессионных моделях? 16. Опишите основные свойства модели адаптивных ожиданий. 17. В чем состоит отличие модели адаптивных ожиданий от модели частичной корректировки? 18. В чем суть метода инструментальных переменных? 19. Приведите общую схему оценивания на основе двухшагового метода наименьших квадратов (ДМНК). 20. По данным за 30 месяцев некоторого временного ряда Охарактеризуйте структуру ряда; составьте наиболее обоснованное уравнение авторегрессии.
Эконометрических уравнений
Для простоты изложения материала будем считать, что системы содержат всего лишь два уравнения. При этом все полученные выводы могут быть обобщены на системы с произвольным числом уравнений и содержащихся в них переменных. В эконометрике принято различать следующие виды систем уравнений [1,28,33]: система независимых уравнений когда каждая зависимая переменная Y рассматривается как функция одного и того же набора факторов-аргументов X:
(7.1)
система рекурсивных уравнений когда зависимая переменная Y одного уравнения представляет собой объясняющую переменную другого уравнения:
(7.2)
система внешне не связанных уравнений:
(7.3)
При этом Cov (1, 2) 0. Данный вид модели может соответствовать экономической ситуации, когда уравнения (7.3) представляют зависимости результирующих экономических показателей различных предприятий, но действующих «в одной экономической среде» (например, компании «Газпром» и «ЛУКойл»). Внешне эти уравнения выглядят как не связанные друг с другом, однако в данной ситуации следует считать случайные отклонения 1 и 2 коррелированными. Отсюда следует, что эффективность оценивания можно повысить, рассматривая эти уравнения совместно; система взаимосвязанных (совместных) одновременных уравнений когда одни и те же зависимые переменные в одних уравнениях одновременно присутствуют в левой части, а в других – в правой:
(7.4)
Такая система уравнений называется структурной формой модели, а параметры a, b, c структурными коэффициентами. В общем случае системы эконометрических уравнений содержат множество взаимосвязанных переменных, которые принято классифицировать как экзогенные, эндогенные и предопределенные. Такая классификация осуществляется в зависимости от содержательной стороны модели и определяет разделение ролей в системе одновременных уравнений. Эндогенными переменными называются взаимосвязанные переменные Y, которые формируются внутри модели (экономического объекта). Экзогенными переменными называются внешние по отношению к модели переменные Х, значения которых определяются вне системы. Предопределенными переменными (т. е. заранее определенными) называются экзогенные и лаговые эндогенные переменные системы. Таким образом, эконометрическая модель в виде системы одновременных уравнений служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных. С точки зрения эконометрического анализа, основное отличие между экзогенными и эндогенными переменными заключается в том, что экзогенные переменные не коррелируют со случайными отклонениями (остатками) регрессии, а эндогенные, как правило, коррелируют. Классическим примером систем одновременных взаимосвязанных уравнений является равновесная модель «спроса-предложения» в рыночной экономике [1,26]:
где Pt цена некоторого товара в момент времени t; It доход в момент времени t; a, b, c неизвестные коэффициенты (параметры модели), которые подлежат определению. Модель содержит два регрессионных (поведенческих) уравнения и одно тождество В соответствии с моделью (7.5) цена и величина спроса и предложения определяются одновременно, подчиняясь соответствующим уравнениям, т. е. формируют свои значения внутри модели. Поэтому обе эти переменные следует считать эндогенными. В отличие от них значения переменной It поступают в систему как характеристики внешней среды, т. е. формируются вне модели. Следовательно, доход является экзогенной переменной. Если с целью совершенствования модели в уравнение предложения ввести переменную Pt 1, определяющую значения цены товара в предыдущий момент времени, то эта переменная и доход It будут являться предопределенными переменными в данной модели.
Оценивание систем уравнений
Для нахождения параметров системы уравнений (7.1) независимо применяется МНК, после чего проводится анализ качества полученных оценок. Системы рекурсивных уравнений (7.2), в которых эндогенные переменные последовательно (рекурсивно) связаны друг с другом, также могут быть оценены с использованием обычного МНК. В этих моделях структурные уравнения оцениваются поэтапно, т. е. на первом этапе оцениваем Y 1, затем Y 2 (в общем случае N уравнений, последовательно Y 1 Y 2 … YN). Наиболее часто в экономике приходится рассматривать системы одновременных уравнений вида (7.4). Если применить к данной системе обычный метод наименьших квадратов, то, как отмечено в разделе 6.2, полученные оценки будут несостоятельными вследствие корреляции эндогенных переменных с остатками регрессии. Поэтому для оценивания систем одновременных уравнений применяют такие специальные методы, как косвенный метод наименьших квадратов, двухшаговый метод наименьших квадратов (ДМНК) в сочетании с методом инструментальных переменных, трехшаговый метод наименьших квадратов [11,28]. Косвенный метод наименьших квадратов (КМНК) основан на использовании приведенных уравнений системы, которые могут быть получены в результате преобразования структурных уравнений и должны содержать в правых частях только экзогенные переменные Х. Процедура КМНК проводится по следующей схеме: 1. Исходя из структурных уравнений системы, строятся уравнения в приведенной форме (приведенная форма модели). 2. Оцениваются по МНК коэффициенты уравнений в приведенной форме. 3. На основе оценок, полученных на этапе 2, которые связаны определенными соотношениями с исходными параметрами, находятся оценки и самих параметров (коэффициентов структурных уравнений). Например, разрешая уравнения системы (7.4) относительно y 1 и y 2, запишем уравнения в приведенной форме:
(7.6)
где (7.7)
Приведенная форма модели представляет собой систему линейных уравнений, в которых эндогенные переменные выражены через все предопределенные переменные исходной системы и случайные отклонения. Далее, применяя к уравнениям (7.6) обычный МНК, получим оценки В рассмотренном примере уравнения (7.7) однозначно разрешимы относительно структурных параметров, что позволяет найти их несмещенные оценки. Очевидно, что подобная ситуация далеко не всегда имеет место. Таким образом, возникает вопрос: при каких условиях можно полностью восстановить структурную форму модели по приведенной? Поставленный вопрос отражает сущность задачи, логически предшествующей оцениванию уравнений, и подводит нас к необходимости рассмотрения проблемы идентификации систем эконометрических уравнений. Исходную систему уравнений называют идентифицируемой (точно определенной), если по коэффициентам приведенных уравнений можно однозначно определить все коэффициенты структурных уравнений. Исходная система называется неидентифицируемой, если хотя бы один из коэффициентов участвующих в ней структурных уравнений не может быть определен (восстановлен) по коэффициентам приведенных уравнений. Исходная система называется сверхидентифицируемой, если по коэффициентам приведенных уравнений определяются все коэффициенты приведенных уравнений, причем один или несколько коэффициентов данной приведенной формы могут одновременно принимать различные числовые значения. Обычно модель является идентифицируемой, когда количество оцениваемых структурных параметров в точности равно количеству оцененных коэффициентов приведенной формы. Проявление сверхидентифицируемости связано с количеством наблюдений: при достаточно большом объеме выборки все различные состоятельные оценки параметра близки к одному и тому же истинному значению. Неидентифицируемость уравнения системы не связана с числом наблюдений и определяется внутренней структурой модели, которая в данном случае формируется таким образом, что общее число структурных коэффициентов превышает число коэффициентов приведенной формы. Для получения необходимых выводов об идентифицируемости структурных уравнений разработаны следующие необходимые и достаточные условия. Если число эндогенных переменных в определенном уравнении системы обозначим через Н, а число предопределенных переменных, которые присутствуют в системе, но не входят в данное уравнение, – через D, то необходимое условие идентифицируемости уравнений модели может быть представлено в виде следующего счетного правила: D + 1 = Н уравнение идентифицируемо; D + 1 < Н уравнение неидентифицируемо; D + 1 > Н уравнение сверхидентифицируемо. Достаточное условие идентифицируемости, вытекающее из общей теории систем линейных уравнений, гласит, что определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не меньше числа эндогенных переменных системы минус единица. Рассмотрение задачи идентифицируемости структурных уравнений необходимо для выбора метода статистического оценивания параметров модели. Для оценки идентифицируемого уравнения системы применяется косвенный метод наименьших квадратов, для оценки сверх– идентифицируемых уравнений – двухшаговый метод наименьших квадратов. Основные понятия двухшагового метода наименьших квадратов (ДМНК) описаны нами в разделе 6.2.2 предыдущей главы. Нетрудно заметить, что в приведенной форме (7.6) экзогенные переменные х 1 и х 2 можно рассматривать как инструментальные для переменных у 1, у 2, не коррелирующие с остатками модели. На практике метод инструментальных переменных применяется в форме ДМНК, который в данном случае осуществляется следующим образом: в качестве инструментальных переменных используются прогнозные значения Для оценивания систем одновременных уравнений может быть применен так называемый трехшаговый метод наименьших квадратов (ТМНК), который учитывает взаимодействие уравнений в системе. Он более эффективен, чем ДМНК, так как позволяет проводить одновременное оценивание всех параметров системы в том случае, когда случайные отклонения различных уравнений системы взаимозависимы. В трехшаговом методе наименьших квадратов сохраняются первые два шага ДМНК. Однако полученные по ДМНК оценки уточняются с помощью одновременного оценивания на третьем шаге. На этом шаге используется обобщенный метод наименьших квадратов, т. е. составляется матричное уравнение системы и оценивается ковариационная матрица остатков всех уравнений, входящих в систему. Затем эта матрица используется для вычисления оценок всех структурных параметров. Процедура ТМНК одновременной оценки всех параметров уравнений системы как внешне не связанных широко применяется в стандартных компьютерных пакетах. Пример 7.1. [31]. Необходимо проверить, является ли идентифицируемой следующая эконометрическая модель[1]:
Модель имеет три эндогенные (у 1, у 2, у 3) и три экзогенные (х 1, х 2, х 3) переменные. Проверим каждое уравнение системы на необходимое и достаточное условия идентифицируемости. Первое уравнение. Необходимое условие: эндогенных переменных – 2 (у 1, у 3), отсутствующих экзогенных – 1 (х 2). Выполняется необходимое равенство: 2 = 1 + 1, следовательно, уравнение точно идентифицируемо. Достаточное условие: в первом уравнении отсутствуют переменные у 2 и х 2. Составим матрицу А из коэффициентов при них в других уравнениях системы:
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо. Второе уравнение: Необходимое условие: эндогенных переменных – 3 (у 1, у 2, у 3), отсутствующих экзогенных – 2 (х 1, х 3). Выполняется необходимое равенство: 3 = 2 + 1, следовательно, уравнение точно идентифицировано. Достаточное условие: во втором уравнении отсутствуют переменные х 1 и х 3. Составим матрицу В из коэффициентов при них в других уравнениях системы:
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации и второе уравнение точно идентифицируемо. Третье уравнение: Необходимое условие: эндогенных переменных – 2 (у 2, у 3), отсутствующих экзогенных – 1 (х 2). Выполняется необходимое равенство: 2 = 1 + 1, следовательно, уравнение точно идентифицируемо. Достаточное условие: в третьем уравнении отсутствуют переменные у 1 и х 2. Составим матрицу С из коэффициентов при них в других уравнениях системы:
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть оценена косвенным методом наименьших квадратов.
Вопросы и упражнения для самопроверки
1. Чем вызвана необходимость использования систем уравнений в эконометрическом моделировании? 2. Что представляют собой системы рекурсивных уравнений? 3. Что представляют собой системы одновременных уравнений? 4. Каким методом проводится оценивание параметров систем рекурсивных уравнений? 5. Как интерпретируется состав переменных в системе одновременных уравнений? 6. Поясните различие между структурной и приведенной формой модели в виде системы регрессионных уравнений. 7. В чем состоит суть косвенного метода наименьших квадратов (КМНК)? 8. Какую проблему необходимо рассматривать при численной оценке параметров структурных уравнений по оценкам коэффициентов приведенных уравнений? 9. Назовите причины сверхидентифицируемости и неидентифицируемсти систем одновременных уравнений. 10. Сформулируйте необходимое и достаточное условия идентифицируемости систем. 11. В чем состоит суть метода инструментальных переменных в форме двухшагового метода наименьших квадратов (ДМНК) при оценивании систем одновременных уравнений? 12. В чем заключается процедура оценивания параметров систем регрессионных уравнений, которая носит название трехшагового метода наименьших квадратов (ТМНК)? 13. Рассматривается система уравнений вида:
Укажите, какие переменные здесь являются экзогенными, а какие – эндогенными. Проверьте, является ли данная система идентифицируемой. Изменится ли ответ, если в число регрессоров второго уравнения включить переменную х?
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.033 с.) |

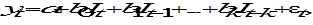 (6.10)
(6.10)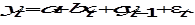 (6.11)
(6.11)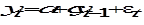 (6.12)
(6.12) , т. е. исследуемая величина Y зависит от ожидаемого значения фактора-аргумента:
, т. е. исследуемая величина Y зависит от ожидаемого значения фактора-аргумента: (6.25)
(6.25)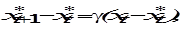 (6.26)
(6.26) значениями переменной Х в предыдущем периоде. Коэффициент 0 1 называется коэффициентом ожидания (адаптации). Если = 0, то ожидания являются неизменными (статичными):
значениями переменной Х в предыдущем периоде. Коэффициент 0 1 называется коэффициентом ожидания (адаптации). Если = 0, то ожидания являются неизменными (статичными):  Если же = 1, то
Если же = 1, то  что означает мгновенно реализуемые ожидания.
что означает мгновенно реализуемые ожидания. (6.27)
(6.27)
 . (6.28)
. (6.28) (6.29)
(6.29) (6.30)
(6.30) .
. . (6.31)
. (6.31) .
.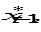 затем для
затем для  и так до бесконечности (итерируя (6.27)), получим соотношение:
и так до бесконечности (итерируя (6.27)), получим соотношение: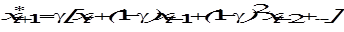 . (6.32)
. (6.32)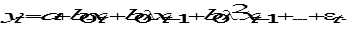 (6.33)
(6.33)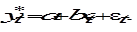 (6.34)
(6.34) не является фактически существующим, то относительно его выдвигается условие частичной корректировки:
не является фактически существующим, то относительно его выдвигается условие частичной корректировки: (6.35)
(6.35)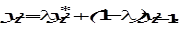 (6.36)
(6.36) равно взвешенному среднему ожидаемого уровня и фактического значения зависимой переменной в предыдущем периоде.
равно взвешенному среднему ожидаемого уровня и фактического значения зависимой переменной в предыдущем периоде. (6.37)
(6.37)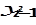 и может быть сведена к модели Койка. Однако для данной модели переменная
и может быть сведена к модели Койка. Однако для данной модели переменная 
 . Их мы теперь будем считать новыми независимыми переменными, и на втором этапе оценка вектора параметров В строится с помощью обычной регрессии Y на
. Их мы теперь будем считать новыми независимыми переменными, и на втором этапе оценка вектора параметров В строится с помощью обычной регрессии Y на 

 (6.38)
(6.38) дисперсия оценки коэффициента при
дисперсия оценки коэффициента при  оценка коэффициента автокорреляции первого порядка, которую можно вычислить по формуле (5.23):
оценка коэффициента автокорреляции первого порядка, которую можно вычислить по формуле (5.23): 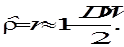

 ;
;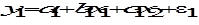
 ;
;

 .
. (уравнение предложения)
(уравнение предложения) (уравнение спроса) (7.5)
(уравнение спроса) (7.5) (условие равновесия рынка),
(условие равновесия рынка),
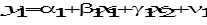
 ,
,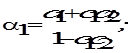



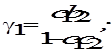
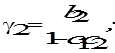



 и
и  . В свою очередь, равенства (7.7) позволяют выразить исходные параметры через,, и получить оценки косвенного метода наименьших квадратов
. В свою очередь, равенства (7.7) позволяют выразить исходные параметры через,, и получить оценки косвенного метода наименьших квадратов  .
.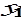 ,
,  переменных у 1, у 2, полученные при оценивании приведенной формы. Затем эти значения подставляются в правую часть структурной формы (7.4) и строятся МНК-оценки структурных коэффициентов. Если система точно идентифицируема, то оценки двухшагового метода наименьших квадратов совпадают с оценками, полученными косвенным методом наименьших квадратов. Очевидно, что в случае сверхидентификации уравнения системы имеется возможность использовать различные наборы инструментальных переменных. Тогда, согласно ДМНК, переменные
переменных у 1, у 2, полученные при оценивании приведенной формы. Затем эти значения подставляются в правую часть структурной формы (7.4) и строятся МНК-оценки структурных коэффициентов. Если система точно идентифицируема, то оценки двухшагового метода наименьших квадратов совпадают с оценками, полученными косвенным методом наименьших квадратов. Очевидно, что в случае сверхидентификации уравнения системы имеется возможность использовать различные наборы инструментальных переменных. Тогда, согласно ДМНК, переменные  должны представлять собой линейные комбинации инструментальных переменных, наиболее тесно коррелирующих с переменными Y.
должны представлять собой линейные комбинации инструментальных переменных, наиболее тесно коррелирующих с переменными Y. .
.

 .
.



