
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие сведения о кинематике и динамике волн.Содержание книги
Поиск на нашем сайте
Однородная изотропная идеально упругая среда. В идеально упругой среде существует линейная связь между напряжениями и деформациями, которая описывается законом Гука. Коэффициенты этой связи называются упругими постоянными среды. Для изотропной среды число независимых упругих постоянных равно двум. Часто употребляются такие пары упругих постоянных ([7], стр. 4-5): 1. Модуль растяжения (модуль Юнга) Е, коэффициент Пуассона 2. Коэффициенты Ламэ 3. Модуль всестороннего сжатия К и модуль сдвига Между ними существуют следующие связи:
В такой среде существуют только два типа упругих волн - продольная (Р) и поперечная (S), скорости которых определяются по формулам:
где Полупространство. Вдоль плоской свободной поверхности однородного твердого полупространства могут распространяться поверхностные волны Релея, траекторией движения частиц в которых является эллипс. Скорость волн Релея определяется скоростями продольной и поперечной волн и их отношением. В целом ([7], стр. 20-21)
В реальных условиях в верхней части разреза существует слой пониженной скорости. Скорость распространяющейся в этом случае псевдорелеевской волны зависит от ее длины, т.е. наблюдается дисперсия скорости. Волны, длина которых Плоские волны и плоские границы раздела При нормальном падении плоской волны (продольной или поперечной) на плоскую границу раздела образуются две монотипные (т.е. такого же типа) волны - отраженная и проходящая. Коэффициент отражения (для смещения частиц)
где
Коэффициент прохождения (для смещений частиц)
Ослабление волны при прохождении границы в прямом и обратном направлении (влияние промежуточной границы на отраженную волну)
При наклонном падении плоской волны на плоскую границу раздела образуются четыре волны - два типа отраженных и два типа проходящих (преломленных) волн. В формулы для коэффициентов отражения и преломления при этом входят значение угла падения и соотношения скоростей волн в обеих средах ([7], стр. 21). Углы отражения и преломления связаны законом Снеллиуса (рис.1)
Идеально упругая среда с объемными неоднородностями. За счет рассеяния на неоднородностях проходящая сейсмическая волна с расстоянием затухает
где
Величина коэффициента рассеяния зависит от размеров и акустической контрастности неоднородностей среды и обычно увеличивается с уменьшением длины волны. Рассеянные волны, накладываясь на проходящие волны, вызывают флуктуации их амплитуд и времен прихода - образуют сейсмическую мутность среды ([7], стр. 73-75). Неидеально упругая среда. В целом, для таких сред закон Гука не справедлив. Однако для изучения распространения сейсмических волн в таких средах можно использовать модифицированный закон Гука, где упругие постоянные имеют комплексную форму и зависят от частоты. В первом приближении изменением скорости волн за счет неидеальной упругости в реальных средах можно пренебречь, а уменьшение амплитуды волн за счет поглощения энергии волн в среде можно учитывать следующим образом:
где
Для большинства сред коэффициент поглощения линейно возрастает с частотой колебаний
где Для некоторых сред эта зависимость близка к квадратичной [5, стр. 56]
Так как затухание сейсмических волн вследствие поглощения их в неидеально упругой среде проявляется во многом так же, как и затухание вследствие рассеяния на неоднородностях среды, то большинство способов определения коэффициентов поглощения по записям сейсмических волн не позволяет разделить эти два эффекта. Поэтому часто говорят об эффективных коэффициентах затухания, включая в это понятие и рассеяние волн. Сферические волны. Плотность энергии сферической волны с удалением от источника уменьшается за счет расхождения фронта волны обратно пропорционально квадрату расстояния
где Поверхностная волна затухает медленнее
Вследствие этого поверхностные волны являются часто сильной помехой в сейсморазведке. При изучении распространения волн с произвольными фронтами в сложнопостроенных средах используются следующие принципы. Принцип Гюйгенса. Каждая точка, до которой дошло возбуждение, является источником вторичных волн; поверхность, огибающая фронты этих вторичных волн, указывает положение фронта действительно распространяющейся волны (рис. 2). Принцип Ферма. Действительный путь распространения волны из одной точки в другую есть тот путь, для прохождения которого волне требуется минимальное (экстремальное) время по сравнению с любым другим путем. Принцип взаимности. Время распространения монотипной волны из одной точки в другую не изменится, если поменять местами источник и приемник.
Годографы волн.
Годограф - это график зависимости времени вступления (экстремума) волны от координат точек наблюдений. Уравнение годографа
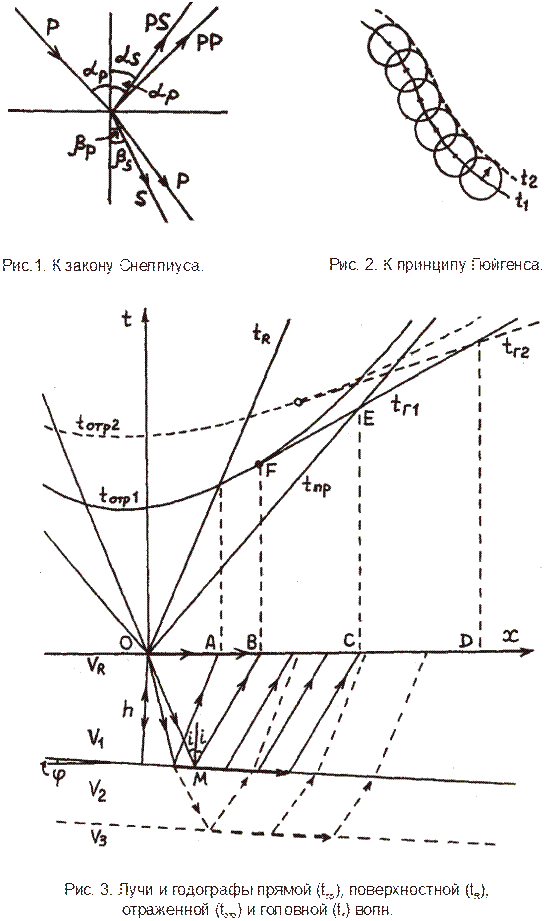
Кажущаяся скорость (V*) - скорость распространения волны вдоль линии наблюдений
Для плоской волны
где
Годограф прямой волны в однородной среде при наблюдении на прямолинейном продольном профиле является наклонной прямой линией (рис. 3). Уравнение годографа
Кажущаяся скорость прямой волны равна истинной скорости
Годограф отраженной волны от плоской отражающей границы, наклоненной под углом
в случае горизонтальной границы принимает вид
Кажущаяся скорость отраженной волны
меняется от
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.84.179 (0.009 с.) |

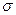 .
.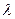 и
и 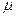 (
(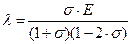 ;
; 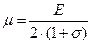 ;
; 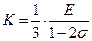 ; (1. 1)
; (1. 1) ;
; 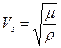 ; (1. 2)
; (1. 2) - плотность среды.
- плотность среды. (1. 3)
(1. 3) (1. 4)
(1. 4) и
и 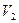 - скорости волн в первой и второй средах;
- скорости волн в первой и второй средах;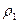 и
и  - плотности первой и второй среды;
- плотности первой и второй среды;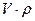 - акустическая жесткость среды.
- акустическая жесткость среды.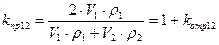 (1. 5)
(1. 5) (1. 6)
(1. 6)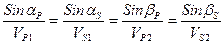 (1. 7)
(1. 7)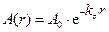 (1. 8)
(1. 8) и
и 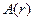 - амплитуды волны в начальной точке среды и на расстоянии
- амплитуды волны в начальной точке среды и на расстоянии 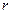 от нее;
от нее; - коэффициент рассеяния.
- коэффициент рассеяния.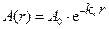 (1. 9)
(1. 9)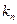 - коэффициент поглощения.
- коэффициент поглощения.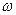 [5, стр. 55]
[5, стр. 55] (1.10)
(1.10) - постоянная поглощения, зависящая от своиств среды.
- постоянная поглощения, зависящая от своиств среды. (1.11)
(1.11) (1.12)
(1.12)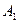 - амплитуды колебаний на расстояния
- амплитуды колебаний на расстояния 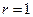 .
.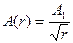 (1.13)
(1.13)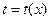
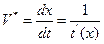 (1.14)
(1.14)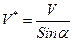 (1.15)
(1.15)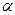 - угол выхода волны на поверхность;
- угол выхода волны на поверхность;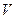 - истинная скорость волны в среде.
- истинная скорость волны в среде.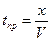 (1.16)
(1.16)
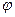 к линии наблюдений, и при однородной покрывающей толще со скоростью
к линии наблюдений, и при однородной покрывающей толще со скоростью  (1.17)
(1.17) (1.18)
(1.18)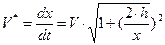 (1.19)
(1.19) при
при 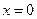 до
до  при
при  .
.


