Назовите основные этапы развития формальной логики.

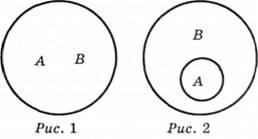
Дайте определение равнозначных понятий.

Равнозначные (тождественные) - это понятия, объемы которых полностью совпадают.

Приме: А - понятие «автор романа «Анна Каренина»»; В – понятие «автор романа «Война и мир»».

Объясните на примере отношение подчинения между понятиями.

Отношение подчинения существует между такими понятиями, одно из которых входит как часть в объем другого. В отношении подчинения находятся, например, понятие "право" и "государственное право". Объем понятия "государственное право" входит в объем понятия «право» как часть его объема. Объем понятия "право" шире, чем объем понятия "государственное право".

 

Объясните на примере отношение перекрещивания (пересечения) между понятиями. Перекрещивающиеся - это понятия, объемы которых частично совпадают. Пример. А – понятие «студент»; В – понятие «спортсмен».

Объясните на примере отношение соподчинения (координации) понятий.

Отношения несовместимых понятий. Отношение соподчинения. Данное отношение возникает между несовместимыми понятиями, имеющими общее родовое понятие, которому все они подчинены. Например, студенты, гимназисты, лицеисты соподчинены в отношении понятия учащиеся; воровство, казнокрадство, коррупция, подлог — в отношении понятия преступление. Как видно из примеров, соподчиненные понятия образуются в результате деления родового понятия на виды. Однако соподчинение не требует обязательного наличия всех видовых понятий, достаточно двух.

Приведите пример двух понятий, находящихся в отношении противоречия (контрадикторности), объясните суть этого отношения.

Отношение противоречия (контрадикторности). Отношение противоречия возникает между такими двумя несовместимыми понятиями, которые вместе составляют объем понятия, выражающего множество вещей, свойств или отношений. При этом между данными понятиями не может быть никаких других, которые не входили бы в их объем. Противоречащие понятия исключают друг друга, но не предполагают, как противоположные. Одно из таких понятий указывает на какие-то признаки, а другое — отрицает их. Таким образом, одно из противоречащих понятий является положительным, а другое — отрицательным. Подобные понятия часто используются как в быту, так и в науке: белый — не белый; сильный — несильный; болезнь — не болезнь; прекрасный — не прекрасный и т. п. Положительным понятиям в составе противоречащей пары можно подобрать противоположные: сильный — слабый; болезнь — здоровье; белый — черный; прекрасный — безобразный. Но эту операцию нельзя произвести с отрицательными понятиями, что демонстрирует принципиальное различие противоположности и противоречия.

Объясните на примере отношение противоположности понятий.

Противоположными (контрарными) понятиями являются такие, которые соподчинены третьему понятию и представляют собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия.

Пример. А – «черный»; В – «белый»; С – «цвет».

Покажите принципиальные отличия таких отношений между понятиями как противоположность и противоречие.

Противоположными (контрарными) понятиями являются такие, которые соподчинены третьему понятию и представляют собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия.

Пример. А – «черный»; В – «белый»; С – «цвет».

Противоречивые (контрадикторные) понятия подчиняются общему для них понятию, и при этом в общем понятии не существует такого элемента, который не был бы элементом одного из этих понятий. Их объемы делят объем общего для них понятия на две части.

Пример. А – «монархия»; В – «республика». Общим для этих понятий является понятие «форма правления». Причем «монархия» и «республика» – несовместимые формы правления, и в то же время других форм правления не существует.

Объясните сферу применения правил вывода в умозаключениях

Вывод — процесс рассуждения, в ходе которого осуществляется переход от некоторых исходных суждений (предпосылок) к новым суждениям — заключениям.

Правила преобразования исходной системы предпосылок в систему заключений называются правилами вывода или правилами проведения умозаключений. Если вид посылок и заключений указан явно, то вывод называется прямым. Если в посылках и заключении указаны лишь виды выводов, от одного из которых разрешается переходить к другому, то вывод называют косвенным.

Понятие вывода используется во многих формальных системах: в логике, математике, информатике, логическом программировании и др. В математической логике правила логического вывода задаются в исчислении высказываний либо исчислении предикатов.

В информатике вывод умозаключений проводится с использованием правил, принципов и законов логического вывода на основе заданных фактов и правил с использованием методов и средств логического программирования.

В информатике для описания фактов и правил логического вывода, а также баз знаний и моделей экспертных систем широко используется язык логического программирования Пролог.

Сформулируйте правила терминов и посылок категорического силлогизма.

Стратегия и тактика спора

Стратегия спора - это общий план его ведения. Нет какой-либо единой и неизменной стратегии спора, поскольку складывающаяся в споре ситуация постоянно меняется и невозможно предугадать все аспекты и нюансы спора; кроме того, в большинстве случаев каждая из спорящих сторон придерживается своей собственной стратегии.
Пропонент - тот, кто выдвигает и отстаивает некоторый тезис - должен позаботиться о том, чтобы обеспечить максимально возможную степень его обоснованности. Для этого необходимо заранее продумать доводы в защиту тезиса, а также последовательность их выдвижения.

Оппонент - это тот, кто оспаривает тезис. Если оппонент заранее ознакомлен с содержанием тезиса или с темой предстоящего обсуждения, ему можно рекомендовать заранее продумать слабые места тезиса и подобрать опровергающие доводы (контраргументы) или сосредоточить свое внимание на проблемных пунктах темы обсуждения и по возможности выработать проекты решения проблемных ситуаций.

Тактика спора - это подбор и использование в споре определенной совокупности логических и психологических приемов. Очевидно, что на разных этапах спора используются и разные тактические приемы. Их характер зависит от многих факторов: содержания спора, состава его участников, интеллектуальных и психологических особенностей спорящих сторон и т.д. Рассмотрим наиболее важные моменты тактики спора.
- Во-первых, в любом споре тактически верным будет корректное поведение его участников.
- Во-вторых, беспроигрышным тактическим приемом является внимательное и доброжелательное отношение к высказываниям противной стороны.
- В третьих, инвариант тактики спора составляет открытость (восприимчивость) одной стороны для убедительных доводов другой.

- В-четвертых, распространен тактический ход, называемый "условное принятие доводов противника". Этот прием позволяет избежать прямого опровержения точки зрения соперника в споре. Условно соглашаясь с доводами противника, мы вместе с ним выводим из его посылок сомнительные следствия, подводя к нужному окончательному выводу.

119) Покажите на примерах и обоснуйте принципиальное отличие паралогизма от софизма.

Логические ошибки бывают содержательными и формальными. Содержательные указывают на несоответствие мысли в той или иной ее форме реальной действительности, а формальные - на нарушение законов и правил образования мысли. Также ошибки делятся на паралогические и софические.

Паралогизмы - это неумышленные логические ошибки, обусловленные нарушением законов и правил логики, это невольные ошибки (по незнанию логики, невнимательности). Паралогизм не является, в сущности, обманом, так как не связан с умыслом подменить истину ложью.

В отличие от паралогизмов софизмы (от древнегреч, «софисма» - «хитрая уловка, выдумка») - результат преднамеренного обмана, умышленные логические ошибки. Софизм представляет собой рассуждение, кажущееся правильным, но содержащее скрытую логическую ошибку и служащее для придания видимости истинности ложному заключению. Софизм является особым приемом интеллектуального мошенничества, попыткой выдать ложь за истину и тем самым ввести в заблуждение. Софизм - не простое явление. На самом деле софизм - один из феноменов мышления, стимулирующее развитие логики.

«Для того чтобы видеть, нет необходимости иметь глаза, так как без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет, поэтому ясно, что глаза не являются необходимыми для зрения» и «Что ты не терял, то имеешь; рога ты не терял, значит, у тебя рога». Последний софизм является одним из самых известных и часто приводится в качестве примера.

120) Покажите на примере и объясните суть приемов в споре «аргумент к публике», «аргумент к жалости», «аргумент к невежеству», «аргумент к «тщеславию» и «аргумент к личности». Проиллюстрируйте примером и объясните логический термин «верификация».

Тот, кто заботится об успешном отстаивании своей позиции в дискуссии, должен, прежде всего, стараться опираться только на истинную информацию и следить за достоверностью информации, предоставляемой противником. Искаженная, как и ложная информация - источник ошибок.

"Внук мне дерзит ", - жалуется бабушка. А внук всего лишь выразил недоумение, что бабушка учит беречь электроэнергию, а сама забывает гасить свет.

Здесь можно еще раз подчеркнуть то, что аргументы должны составлять достаточное основание для тезиса: во-первых, относиться к рассматриваемой области, во-вторых, давать в совокупности достаточную информацию для подтверждения тезиса. Вряд ли кто-нибудь по здравом размышлении скажет, что обнаружение платка Дездемоны у одного из друзей

семьи - уместный и решающий аргумент в пользу измены Дездемоны (измены, существовавшей лишь в голове ревнивого Отелло). Но молодая женщина оказалась все же задушенной своим горячо любимым мужем, так и не успев доказать свою верность.

А ведь если человек способен заключить о ложности тезиса только на том основании, что еще не доказана его истинность, то он вполне оправдывает старинное название еще одной логической ошибки: " аргументация к невежеству ".

" Аргументация к личности " (или: апелляция к личности, довод к личности) при обосновании утверждений о поступках некоего человека приводит в качестве аргументов высказывания об этом человеке, к конкретному поступку не относящиеся, но составляющие эмоционально отталкивающий образ человека. Дмитрий Карамазов - пьяница, буян, угрожал убить отца, бросил невесту ради особы сомнительного поведения и т.д.

Слабость обоснования не всегда прячется за спину одного авторитета, иногда она стремится " раствориться в толпе ". Доказательство подменяется ссылкой на якобы общую признанность точки зрения, а то и на стереотипные представления, житейскую мудрость пословицы: " Всем хорошо известно, что...", "Даже ребенку ясно, что...", "Плетью обуха не перешибешь, поэтому..." - «аргумент к публике».

«Аргумент к жалости»

возбуждение в другой стороне спора жалости и сочувствия с намерением получить ее поддержку.

Напр., школьник, не выучивший урок, просит не ставить ему двойку, потому что дома бабушка, узнав об этом, очень расстроится (см.:Эристика

).

«Аргумент к тщеславию»

Расточение неумеренных похвал противнику в споре в расчете, что, тронутый ими, он станет мягче и покладистее.

Этот довод можно считать частным случаем аргумента к личности. Как только в споре начинают встречаться обороты типа "не подлежит сомнению глубокая эрудиция оппонента", "как человек выдающихся достоинств, оппонент...", можно предполагать завуалированный А. к т. (см.: Эристика).

Верификация

(от лат. verificatio - доказательство, подтверждение) понятие, используемое в логике и методологии научного познания для обозначения процесса установления истинности научных утверждений посредством их эмпирической проверки. Проверка заключается в соотнесении утверждения с реальным положением дел с помощью наблюдения, измерения или эксперимента. Различают непосредственную и косвенную В. При непосредственной В. эмпирической проверке подвергается само утверждение, говорящее о фактах действительности или экспериментальных данных. Однако далеко не каждое утверждение может быть

непосредственно соотнесено с фактами, ибо большая часть научных утверждений относится к идеальным, или абстрактным, объектам. Такие утверждения верифицируются косвенным путем. Из данного утверждения мы выводим следствие, относящееся к таким объектам, которые можно наблюдать или измерять. Это следствие верифицируется непосредственно. В. следствия рассматривается как косвенная В. того утверждения, из которого данное следствие было получено. Напр., пусть нам нужно верифицировать утверждение "Температура в комнате равна 20°С". Его нельзя верифицировать непосредственно, ибо нет в реальности объектов, которым соответствуют термины "температура" и "20°С". Из данного утверждения мы можем вывести следствие, говорящее о том, что если в комнату внести термометр, то столбик ртути остановится у отметки "20". Мы приносим термометр и непосредственным наблюдением верифицируем утверждение "Столбик ртути находится у отметки "20"". Это служит косвенной В. первоначального утверждения.

 

Назовите основные этапы развития формальной логики.

Формальная логика в своем развитии прошла два основных этапа.

Первый этап - это связь с работами Аристотеля, в которых дано систематическое изложение логики. Основным содержанием логики Аристотеля является теория дедукции, также содержаться элементы математической логики. Аристотель сформулировал основные законы мышления: тождества, противоречия и исключенного третьего, описал важнейшие логические операции, разработал теорию понятия и суждения, обстоятельно исследовал дедуктивное умозаключение. Учение о силлогизме составило основу одного из направлений современной математической логики - логике предикатов. Дополнением к этому учению была логика античных стоиков (Зенон, Хрисипп и других). Логика стоиков - основа другого направления математической логики - логики высказываний. Следующими, кто развил учение Аристотеля, следует назвать Галена; Порфирия, который разработал схему отображающую отношения между понятиями; Боэция, сочинения которого были логическими пособиями. Логика развивалась и в средние века, однако схоластика исказила учение Аристотеля, приспособив его для обоснования религиозной догматики. Значительны успехи логической науки в Новое время. Важнейшим этапом в ее развитии явилась теория индукции, разработанная Ф. Беконом. Он подверг критике дедуктивную логику, которая не может служить методом научных открытий. Методом должна быть индукция. Разработка индуктивного метода - огромная заслуга Бекона. Методы дедукции и индукции не исключают друг друга, а дополняют. Дж.С.Милль систематизировал методы научной индукции. Дедуктивная логика Аристотеля и индуктивная логика Бекона - Милля составили основу общеобразовательной дисциплины и составляют основу логического образования в настоящее время.

Второй этап - это появление математической логики. Философ Г.В. Лейбниц считается основоположником. Он пытался построить универсальный язык, с помощью которого споры между людьми можно было разрешить посредством вычисления. Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного вывода. Для выявления структуры вывода строят различные математические исчисления.

Другим основанием деления логики служит различие применяемых в ней принципов, на которых базируются исследования. В результате такого деления имеем классическую логику и неклассические логики. В.С. Меськов выделяет принципы классической логики: ”1) область исследования составляют обыденные рассуждения; 2) допущение о разрешимости любой проблемы; 3) отвлечение от содержания высказываний и от связей по смыслу между ними; 4) абстракция двузначности высказываний”.

11)Дайте определение категории «знак».

Знак - это любой чувственно воспринимаемый предмет, выступающий представителем другого предмета. Среди различных знаков выделим два вида: знаки-образы и знаки-символы.

Знаки-образы имеют определённое сходство с обозначаемыми предметами. Примеры таких знаков: копии документов, фотоснимки. Знаки-символы не имеют сходства с обозначаемыми предметами. Например: нотные знаки, знаки азбуки Морзе, буквы.

Множество исходных знаков составляет его алфавит.

12. Имя это языковое выражение для обозначения предмета. Имя предмета может быть простым (туризм, рынок), сложным (денежная система), собственным, общим (туристическая компания).
Каждое имя имеет значение - денотат и смысл имени - концепт. Термином называется слово или словосочетание, которое точно обозначает определенный предмет. Значение имени это обозначаемый данным именем предмет (менеджер, турист). Смысл имени это способ обозначения имени предмета, более точная фиксация его содержания. Денотату туризм соответствует концепт: путешествие с целью отдыха.

13) По составу различают имена простые, которые не включают других имен (государство), и сложные, включающие другие имена (спутник Земли)

14 СЕМАНТИЧЕСКИЕ КАТЕГОРИИ — типы значений выражений языка. Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно разбить на так называемые семантические категории, к которым относятся: 1) предложения: повествовательные, побудительные, вопросительные; 2) выражения, играющие определенную роль в составе предложений: дескриптивные и логические термины'.

Конъюнкция соответствует сонму “и”. Конъюнктивное высказывание обозначается: a ^ b, или а • b, или а & b (например, “Закончились лекции (а), и студенты пошли домой (b)”¹.

Дизъюнкция соответствует союзу “или”. Дизъюнктивное суждение обозначается: a v Ь (нестрогая дизъюнкция) и a v b (строгая дизъюнкция); отличие их в том, что при строгой дизъюнкции сложное суждение истинно только в том случае, когда истинно одно из составляющих суждений, но не оба, а при нестрогой дизъюнкции истинными могут быть одновременно оба суждения. “Он шахматист или футболист” обозначается как а v b. “Сейчас Петров находится дома или в институте” обозначается как а b.

Импликация соответствует союзу “если... то”. Условное суждение обозначается: а → b. (например: “Если будет хорошая погода, то мы пойдем в лес”).

Эквиваленция соответствует словам “если и только если”, “тогда и только тогда, когда”, “эквивалентно”. Эквивалентное высказывание обозначается: а ≡ b, или а ↔ b, или а →← b.

Отрицание соответствует словам “не”, “неверно, что”. Отрицание высказывания обозначается: ā, ┐а, ~а [например: “Падает снег” (а); “Неверно, что падает снег” (ā)].

Квантор общности обозначается и соответствует кванторным словам “все” (“всякий”, “каждый”, “ни один”). хР(х) - запись в математической логике. (Например, в суждении “Все красные мухоморы ядовиты” кванторное слово “все”).

Квантор существования обозначается и соответствует словам “некоторые”, “существует”. хР(х) - запись в математической логике. (Например, в суждениях “Некоторые люди имеют высшее образование” или “Существуют люди, которые имеют высшее образование” - кванторные слова выделены курсивом).

15) Основными логическими приемами формирования понятий являются анализ, синтез, сравнение, абстрагирование, обобщение. (Понятие - это форма мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов).

Анализ - мысленное расчленение предметов на их составные части, мысленное выделение в них признаков.

Синтез - мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа.

Сравнение - мысленное установление сходства или различия предметов по существенным или несущественным признакам.

Абстрагирование - мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделении существенных признаков и в отвлечении от несущественных, второстепенных.

Обобщение - мысленное объединение однородных предметов в некоторый класс.

16. Функции понятий
Понятие является представителем некоторого класса — это определенная совокупность признаков, которые мы ассоциируем с этим классом.
В умственной деятельности понятия выполняют несколько важных функций.
Одна из них состоит в содействии когнитивной экономии путем деления мира на единицы, которыми можно манипулировать. Мир наполнен таким множеством различных объектов, что если бы мы рассматривали каждый из них как нечто отдельное, то очень скоро потерялись бы в этом множестве. Рассматривая различные объекты как представителей одного и того же понятия, мы уменьшаем сложность мира, который нам надо представлять мысленно.
Вторая важная функция понятий: они позволяют предсказывать информацию, которую сразу нельзя воспринять. Например, понятие «яблоко» связано с такими трудновоспринимаемыми свойствами, как наличие семян и съедобность, а также с такими легко видимыми свойствами, как округлость, определенный цвет и местонахождение на дереве. Видимыми свойствами можно воспользоваться, чтобы категоризовать некоторый объект как «яблоко» (объект красный, круглый и висит на дереве), а затем заключить, что он обладает и менее видимыми свойствами яблока (в нем есть семечки и он съедобен). Понятия, таким образом, позволяют выйти за пределы данной информации
Есть также понятия о действиях (например, «съесть»), состояниях (например, «быть старым») и абстракциях (например, «правда», «справедливость» или даже число «два»). В каждом случае мы кое-что знаем о признаках, общих для представителей данного понятия. Широко применяемые понятия, вроде только что приведенных, ассоциируются с названием, состоящим из одного слова. Это позволяет быстро обмениваться переживаниями, которые возникают часто. Понятия можно также формировать «на месте», для какой-либо определенной цели. Если, например, вы планируете поездку за город, можно создать понятие «что нужно взять для поездки с ночевкой». Подобные целенаправленные понятия облегчают планирование. Хотя они используются относительно нечасто и у них, соответственно, относительно длинные названия, они все же создают определенную когнитивную экономию и обладают предсказательными

17-19 (Приведите пример универсального класса, укажите основное отличие универсальных классов.

Приведите пример единичного класса, дайте логические характеристики единичного класса.

Приведите пример нулевого класса, объясните саму возможность их существования.)
Классом, или множеством, называется определенная совокупность предметов, имеющих некоторые общие признаки. Таковы, например, классы (множества) высших учебных заведений, студентов, юридических законов, преступлений и т.д. На основании изучения определенного класса предметов формируется понятие об этом классе. Так, на основе изучения класса (множества) юридических законов образуется понятие юридического закона. Класс (множество) может включать в себя подкласс, или подмножество. Например, класс студентов включает в себя подкласс студенток юридических вузов, класс преступлений — подкласс экономических преступлений. Отношение между классом (множеством) и подклассом (подмножеством) является отношением включения и выражается при помощи знака с: А с В. Это выражение читается: А является подклассом В. Так, если А — следователи, а В — юристы, то А будет подклассом класса В. Классы (множества) состоят из элементов. Элемент класса — это предмет, входящий в данный класс. Так, элементами множества высших учебных заведений будут Московский государственный университет им. М.В. Ломоносова, Московская государственная юридическая академия и т.д.
Различают универсальный класс, единичный класс и нулевой, или пустой, класс.
Класс, состоящий из всех элементов исследуемой области, называется универсальным классом (например, класс планет Солнечной системы).
Если класс состоит из одного элемента, то это будет единичный класс (например, планета Юпитер);
класс, который не содержит ни одного элемента, называется нулевым (пустым) классом. Пустыми классами являются, например, вечный двигатель, круглый квадрат, русалка, леший

20.Закон обратного отношения между объемами и содержаниями понятий
В этом законе речь идет о понятиях, находящихся в родовидовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть.
Например, объем понятия “хищная рыба” целиком входит в объем другого, более широкого по объему понятия “рыба” (составляет часть объема понятия “рыба”). При этом содержание пер-вого понятия оказывается шире, богаче (содержит больше признаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем понятия, тем уже его содержание, и наоборот. Этот закон называется законом обратнох-о отношения между объемами и содержаниями понятий. Он указывает на то, что чем
меньше информации о предметах, заключенной в понятии, тем шире класс предметов и неопределеннее его состав (например, “водопад”), и наоборот, чем больше информации в понятии (например, “крупный водопад” или “крупный водопад в Канаде”), тем уже и определеннее круг его предметов, или даже мыслится только один предмет.

21 В языке понятия выражаются посредством слов или словосочетаний (групп слов).
Существуют слова-омонимы, имеющие различное значение, выражающие различные понятия, но одинаково звучащие (например, слово “коса” в смысле девичья коса, или как орудие труда, или как песчаная отмель).
Существуют слова-синонимы, имеющие одинаковое значение, т. е. выражающие одно и то же понятие, но различно звучащие (например, око - глаз, враг - недруг, хворь - болезнь и др.).

22. Дайте определение конкретных и абстрактных понятий.

Конкретными являются понятия о предметах, а абстрактными – о свойствах и отношениях. Например, конкретными являются понятия: «машина», «дом», «дорога», «деньги» и т.п.; абстрактными понятиями являются: «стойкость», «красота», «надежность», «сила», «координация», «субординация» и т.п.

23. Дайте определение положительных и отрицательных понятий.

Отрицательными называются понятия, в содержании которых указывается на отсутствие у предмета определенных свойств (например, "некрасивый поступок", "некрашеный дом", "некошеный луг" и др.). В русском языке отрицательные понятия выражаются обычно словами с отрицательными приставками "не" или "без" ("бес"): "неграмотный", "неверующий", "беззаконие", "беспорядок" и др. В словах иностранного происхождения - чаще всего словами с отрицательной приставкой "а": "агностицизм", "аморальный" и др. «не-человек»
Положительные - это понятия, содержание которых составляют свойства, присущие предмету: "принципиальность", "благородный поступок", "живущий по средствам", "успевающий студент" и др.

24. Дайте определение соотносительных и безотносительных понятий.

Если в понятии отражаются (обобщаются) предметы, которые предполагают существование других, родственных, предметов, то говорят о соотносительных понятиях. Например, такие понятия, как «отец», «родитель», «начальник», предполагают существование других людей, которые являются соответственно «ребенком», «рожденным», «подчиненным».
Безотносительные - такие понятия, предметы в которых мыслятся как существующие самостоятельно, сами по себе, независимо от того, в каком отношении они находятся с другими предметами. Например, «человек» (как существо, способное трудиться, мыслить и говорить), «кража» (как особые деяния, которые совершаются тайно и состоят в хищении чужого имущества).

25. Дайте определение собирательных и несобирательных понятий.

Собирательное понятие - такое, в котором мыслятся множества предметов, составляющих единое целое («коллектив», «армия», «группа учащихся»). Объем собирательного понятия составляют множества предметов, например множество членов коллектива, множество военнослужащих в армии. Содержание собирательного понятия составляют существенные признаки, относящиеся ко всей совокупности элементов, но не к каждому элементу.
Собирательные понятия могут быть общими («коллектив», «народ» и т. п.) и единичными («созвездие Большой Медведицы», «население города Москвы»).
В несобирательных единичных и общих понятиях содержание (совокупность существенных признаков) относится к каждому элементу объема понятия. Например, несобирательными общими понятиями являются: «преступление», «кража», «человек», а несобирательными единичными понятиями являются: «основатель Москвы Юрий Долгорукий», «первый космонавт Юрий Гагарин» и др.

26. Приведите пример и объясните суть пустых понятий.

Пустыми называются понятия, которым не соответствует ни один предмет в объективном мире. Например, «вечный двигатель», «эфир» (не легкая жидкость, а материальная субстанция), «кентавр», «звездолет», «терминатор» и т.п.

27. Дайте определение непустых понятий.

Соответственно, непустыми являются понятия, соответствующие каким-либо предметам действительности; например: «Млечный путь», «страны СНГ», «теория относительности», «кафедра философии» и т.п.

Приведите пример и объясните суть логически сравнимых и несравнимых понятий.

Сравнимые и несравнимые понятия. Сравнимыми называют понятия, в содержании которых имеется хотя бы один общий признак. Почти все понятия являются сравнимыми. В данном случае опровергается известная пословица «Нельзя сравнивать Божий дар с яичницей». С точки зрения логики, это также сравнимые понятия, так как о них, по крайней мере, можно сказать, что и то, и другое – предмет. Это и будет их общий признак. Несравнимыми называют понятия, в содержании которых нет ни одного общего признака. Некоторые авторы в качестве примера несравнимых понятий приводят понятия «предмет» и «свойство». Сравнимые понятия могут быть совместимыми или несовместимыми.

Приведите пример и объясните суть совместимых понятий.

Понятия называются совместимыми, если их объемы имеют хотя бы один общий элемент. Несовместимые – это понятия, в объемах которых нет ни одного общего элемента. Обычно отношения между понятиями изображают с помощью так называемых кругов Эйлера. Виды совместимых понятий. Совместимые понятия могут быть равнозначными (тождественными), перекрещивающимися, а также подчиненным и подчиняющим.