
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розробити модель центру ІТ – технологій і дослідити поведінку характеристик і ефективності.Содержание книги
Поиск на нашем сайте
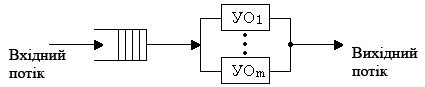
В центр ІТ - технологій з r комп’ютерами надходять замовлення на обчислювальні роботи від різних фірм. Якщо всі комп’ютери зайняті роботою, то замовлення, що поступає до центру, не приймається і фірма змушена звертатися в інше місце. Середній час виконання замовлення складає 3 год. Інтенсивність потоку заявок є величина λ. Дана система належить до багатоканальних систем масового обслуговування з відмовами. Багатоканальні СМО – це СМО з декількома однаковими пристроями обслуговування, що ввімкнені паралельно (мал. 2.4).
Аналіз багатоканальних СМО набагато складніший, ніж одноканальних. За допомогою теорії масового обслуговування можна отримувати аналітичні залежності в замкнутому вигляді для розрахунку характеристик роботи багатоканальних СМО в стаціонарному режимі роботи тільки лише для моделей типу Для системи, що складається з
Його можна трактувати як математичне очікування числа зайнятих пристроїв. Розглянемо класичне завдання Эрланга. Є п каналів, на які поступає потік заявок з інтенсивністю Система S (СМО) має наступні стани (нумеруємо їх по числу заявок, що знаходяться в системі): So, S1, S2,..., Sk..., Sn, де Sk — стан системи, коли в ній знаходиться k заявок, тобто зайнято k каналів. Граф станів СМО відповідає процесу загибелі і розмноження показаний на мал. 2
   … … 
Мал. 2
Потік заявок послідовно переводить систему з будь-якого лівого стану в сусідній правий з однією і тією ж інтенсивністю Для схеми загибелі і розмноження одержимо для граничної вірогідності стану
де члени розкладання Величина
Формула (а) для граничної вірогідності одержала назву формула Эрланга на честь засновника теорії масового обслуговування. Вірогідність відмови СМО є гранична вірогідність того що всі п каналів системи будуть зайняті, тобто
Відносна пропускна спроможність — вірогідність того, що заявка буде обслужена:
Середнє число зайнятих каналів є математичне очікування числа зайнятих каналів:
де pk — гранична вірогідність станів, визначуваних по формулі (8). Проте середнє число зайнятих каналів можна знайти простіше, якщо врахувати, що абсолютна пропускна спроможність системи А є не що інше, як інтенсивність потоку обслужених системою заявок (у одиницю часу). Оскільки кожен зайнятий канал обслуговує в середньому заявок (у одиницю часу), то середнє число зайнятих каналів
або
Складаємо ланцюг Маркова для даної системи:
Вихідні параметри: λ=0,7;r=3; µ=3
Висновок:
як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%.
Висновок У цій курсовій роботі розкриті поняття, що пояснюють функціонування системи масового обслуговування. Чітко розписані змодельовані процеси обслуговування, які дають чітке поняття про оптимізацію систем масового обслуговування. Також описані типові елементи, з яких складаються системи масового обслуговування (потік, що входить, його опис і основні особливості, черга і її дисципліна, обслуговуючі прилади і особливості механізму обслуговування, потік, що входить). Провівши дослідження СМО з кількістю каналів 3, інтенсивністю друку 0,9, і середньому часі обслуговування ми зробили висновок, що дана СМО гн є ефективною, оскільки коефіцієнт простою каналів 92,5%. Можна запропонувати внести зміни для покращення роботи СМО. А саме: зменшити кількість каналів до 1 і швидкість обслуговування до 2 хв. (поставити один принтер, більш дорогий який може друкувати з більшою швидкістю) зміни, що до інтенсивності ми вносити не можемо, отже вона залишається незмінною. Результати наших початкових досліджень наведені в таблиці, також там присутні запропоновані зміни по яким видно, що коефіцієнт простою каналів зменшився до 55%. Розглянувши таблицю нам чітко видно, що наші пропозиції доцільно застосувати, що покращить роботу СМО. Як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%. Дослідивши розроблену модель і основні показники роботи менеджера ми дійшли до висновку, що потрібно змінити вхідні параметри, щоб оптимізувати процес. За заданими параметрами ми отримали результати: Імовірність простою техніка Р0=2,04%,Коефіцієнт простою комп’ютера α=67,35%, Коефіцієнт очікування обслуговування β=47,75%,Середній час очікування Т=7,163121 хв. Розглянувши декілька варіантів внесення змін до даної СМО (приклади наведені в таблиці) ми зробили висновок, що доцільно зменшити кількість комп’ютерів до 4, що в свою чергу дасть нам збільшення простою техніка до 6,24% робочого часу, що не дуже багато, але це ж дасть нам змогу зменшити коефіцієнт простою комп’ютерів до 60,94% і коефіцієнт очікування обслуговування до 37,50%. Факт зменшення кількості комп’ютерів позитивно вплинув на процес, оскільки наші комп’ютери будуть більше працювати ніж простоювати, і відповідно утримувати 4 комп’ютери економічно вигідніше ніж 5. Якщо змінювати інтенсивність надходження вимог, то отримуємо залежність відповідно до якої збільшення інтенсивності надходження вимог призводить до погіршення роботи системи. Звідси випливає, що заданий параметр інтенсивності надходження вимог (5 вимог на годину) цілком об’єктивний і чітко підходить для оптимальної роботи системи. Як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.008 с.) |

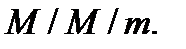 Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи.
Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи. однакових пристроїв обслуговування коефіцієнт завантаження дорівнює:
однакових пристроїв обслуговування коефіцієнт завантаження дорівнює: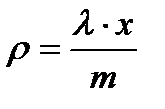
 . Потік обслуговувань має інтенсивність
. Потік обслуговувань має інтенсивність 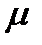 . Знайти граничну вірогідність станів системи і показники її ефективності.
. Знайти граничну вірогідність станів системи і показники її ефективності.

 …
… 
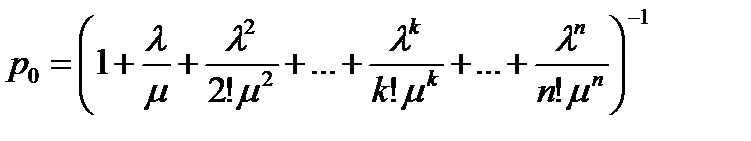
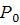 називається приведеною інтенсивністю потоку заявок або інтенсивністю навантаження каналу. Вона виражає середнє число заявок, що приходить за середній час обслуговування однієї заявки. Тепер
називається приведеною інтенсивністю потоку заявок або інтенсивністю навантаження каналу. Вона виражає середнє число заявок, що приходить за середній час обслуговування однієї заявки. Тепер (а)
(а)

 Абсолютна пропускна спроможність:
Абсолютна пропускна спроможність:



















 7,8%
7,8%



