
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математичне введення в теорію ланцюгів Маркова. (Markov’schain)Содержание книги
Поиск на нашем сайте
Дискретні ланцюги Маркова. Говоритимемо, що заданий дискретний ланцюг Маркова, якщо для послідовності випадкових величин виконується рівність Це означає, що потік випадкових величин визначається тільки вірогідністю переходу від попереднього значення випадкової величини до подальшого. Знаючи початковий розподіл вірогідності, можна знайти розподіл на будь-якому кроці. Величини in можна інтерпретувати як номери станів деякої динамічної системи з дискретною безліччю станів (типу кінцевого автомата). Якщо вірогідність переходів не залежить від номера кроку, то такий ланцюг Маркова називається однорідним і її визначення задається набором вірогідності Для однорідного Марківського ланцюга можна визначити вірогідність переходу із стану i в стан j за m кроків
Ланцюг Маркова називається тією, що не приводиться, якщо кожний її стан може бути досягнутий з будь-якого іншого стану. Стан i називається поглинаючим, якщо для нього pii =1. Стан називається поворотним, якщо вірогідність попадання в нього за кінцеве число кроків рівна одиниці. В іншому випадку стан відноситься до неповоротних. Поворотний стан може бути періодичним і аперіодичним залежно від наявності кратних кроків повернення. Введемо вірогідність повернення в стан i через n кроків після відходу з цього стану: Вони дозволяють визначити середнє число кроків або, інакше кажучи, середній час повернення: Стан називається поворотним нульовим, якщо середній час повернення в нього рівно нескінченності, і поворотним ненульовим, якщо цей час звичайно. Відомі дві важливі теореми: Теорема 1 Стани ланцюга Маркова, що не приводиться, або всі неповоротні, або всі поворотні нульові, або всі поворотні ненульові. У разі періодичного ланцюга всі стани мають один і той же період. Друга теорема розглядає вірогідність досягнення станів в стаціонарному (тобто не залежному від початкового розподілу вірогідності) режимі. Відповідний розподіл вірогідності також називають стаціонарним. Знаходження стаціонарного розподілу вірогідності досягнення станів одна з основних задач теорії телетрафіка.
Теорема 2 Для ланцюга Маркова, що не приводиться і аперіодичної, завжди існує гранична вірогідність, не залежна від початкового розподілу вірогідності. Більш того, має місце одна з наступних двох можливостей:
А) всі стани ланцюга неповоротні або всі поворотні нульові, і тоді вся гранична вірогідність рівна нулю і стаціонарного стану не існує; Б) всі стани поворотні ненульові і тоді існує стаціонарний розподіл вірогідності:
Стан називається ергодичним, якщо воно аперіодичне і поворотно-ненульове. Якщо всі стани ланцюга Маркова ергодичні, то весь ланцюг називається ергодичним. Граничну вірогідність ергодичного ланцюга Маркова називають вірогідністю стану рівноваги, маючи на увазі, що залежність від початкового розподілу вірогідності повністю відсутня. Ланцюг Маркова з кінцевим числом станів (кінцевий ланцюг), зручно зображати у вигляді орієнтованого графа, званого діаграмою переходів. Вершини графа асоціюються із станами, а ребра з вірогідністю переходів. Обчислення вірогідності досягнення станів проводиться прямими методами або за допомогою z-перетворення.
Ланцюг Маркова Введемо матрицю вірогідності переходів і вектор-рядок вірогідності на кроці n
Розподіл вірогідності на довільному кроці тоді підкорятиметься матричному співвідношенню:
Воно дозволяє рекурентно обчислювати всю вірогідність станів. Для знаходження граничного розподілу (стаціонарного) потрібно вирішити рівняння:
Його можна вирішувати як систему лінійних рівнянь алгебри, якщо ланцюг кінцевий. Для прикладу (мал. 1) маємо:
і рішення матричного рівняння зводиться до рішення системи трьох рівнянь:
Коефіцієнти першого рівняння в цій системі доповнюють до одиниці суму коефіцієнтів другого і третього рівнянь; це свідчить про лінійну залежність між ними. Тому для вирішення системи рівнянь потрібно ввести додаткову нормуючу умову. В даному прикладі: Вирішуючи систему отриманих рівнянь, маємо:
Рівняння для вірогідності досягнення стану в перехідному режимі вирішити значно важче. Деякого спрощення можна досягти, використовуючи z – перетворення. Застосуємо його до рівняння для перехідної вірогідності
Позначаючи відповідні перетворення, отримаємо: Всі отримані тут математичні результати відносилися до однорідних Марківських процесів, де вірогідність переходів не залежить від часу. В більш загальному випадку така залежність має місце.
Розглянемо вірогідність переходу системи із стану i на m-том кроці в стан j на n-том кроці для n > m. Можна показати, що ця вірогідність зв'язана між собою, так званим рівняннями Чепмена-Колмогорова. (Chapman – Kolmogorov)
Для однорідних ланцюгів Маркова ці рівняння спрощуються оскільки
І зводяться до аналізованих вище.
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.01 с.) |

 .
.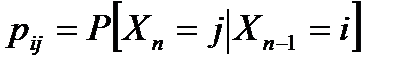 .
.

 .
.

 .
. .
.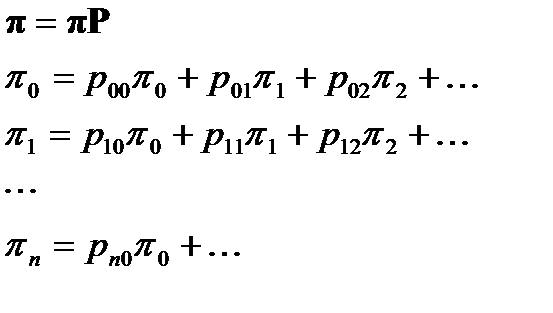
 .
.
 .
.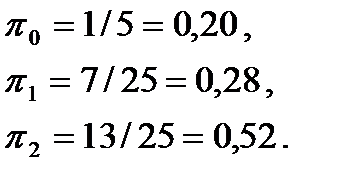
 .
. .
. .
.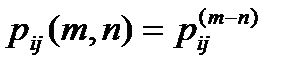 .
.


