
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Керівник проекту: Коваль Т.В.Содержание книги Поиск на нашем сайте
КУРСОВИЙ ПРОЕКТ з дисципліни «Моделювання систем» Допущений до захисту Виконав: «___»___________2012р. студент ІІІ курсу, групи КНСК 12 Захищений Спеціальність 6.050101 «__________________» Романчук Я.А. «___»______________2012р. Керівник проекту: Коваль Т.В. Київ-2012 Зміст Вступ 3 Моделювання, основні його задачі. 4 Математичне введення в теорію ланцюгів Маркова. (Markov’schain) 7 Системи масового обслуговування 11 Практична частина 15 Висновок 27 Список використаної літератури 29 Додатки 30
Вступ Аналітичні методи дослідження операцій здаються на перший погляд універсальними засобами для моделювання різноманітних явищ і процесів, які існують в житті. Але це не так, оскільки вони є надзвичайно динамічними, складними, різноманітними. Виходом з такого положення може здатися застосування математичних моделей, але за допомогою них не завжди можна вирішувати усі завдання які постають перед нами. Математичні моделі які можуть бути реалізовані за допомогою ефективних обчислювальних методів, є надто спрощені, а отже не адекватні реальним процесам. Що ж до адекватних математичних моделей то їх здебільшого не можна реалізувати через труднощі обчислювального характеру. У такому разі є сенс застосувати машинну імітацію, що полягає в моделюванні на ЕОМ реальної виробничої чи економічної системи. Машинна імітація дає змогу користувачеві проводити такі експерименти, які з існуючими реальними системами були б не можливі. Такий метод набуває сьогодні особливої ваги, насамперед як інструмент удосконалення управління економікою та її галузями в межах усієї України. Є всі підстави стверджувати, що машинна імітація – один з найзагальніших та найпотужніших методів прикладного системного аналізу. Адже з допомогою імітаційних моделей системи розкривається сутність відповідних явищ і процесів за умови, що натуральні досліди в реальному середовищі на реальних об’єктах виключаються.
Математичне введення в теорію ланцюгів Маркова. (Markov’schain) Дискретні ланцюги Маркова. Говоритимемо, що заданий дискретний ланцюг Маркова, якщо для послідовності випадкових величин виконується рівність Це означає, що потік випадкових величин визначається тільки вірогідністю переходу від попереднього значення випадкової величини до подальшого. Знаючи початковий розподіл вірогідності, можна знайти розподіл на будь-якому кроці. Величини in можна інтерпретувати як номери станів деякої динамічної системи з дискретною безліччю станів (типу кінцевого автомата). Якщо вірогідність переходів не залежить від номера кроку, то такий ланцюг Маркова називається однорідним і її визначення задається набором вірогідності Для однорідного Марківського ланцюга можна визначити вірогідність переходу із стану i в стан j за m кроків
Ланцюг Маркова називається тією, що не приводиться, якщо кожний її стан може бути досягнутий з будь-якого іншого стану. Стан i називається поглинаючим, якщо для нього pii =1. Стан називається поворотним, якщо вірогідність попадання в нього за кінцеве число кроків рівна одиниці. В іншому випадку стан відноситься до неповоротних. Поворотний стан може бути періодичним і аперіодичним залежно від наявності кратних кроків повернення. Введемо вірогідність повернення в стан i через n кроків після відходу з цього стану: Вони дозволяють визначити середнє число кроків або, інакше кажучи, середній час повернення: Стан називається поворотним нульовим, якщо середній час повернення в нього рівно нескінченності, і поворотним ненульовим, якщо цей час звичайно. Відомі дві важливі теореми: Теорема 1 Стани ланцюга Маркова, що не приводиться, або всі неповоротні, або всі поворотні нульові, або всі поворотні ненульові. У разі періодичного ланцюга всі стани мають один і той же період. Друга теорема розглядає вірогідність досягнення станів в стаціонарному (тобто не залежному від початкового розподілу вірогідності) режимі. Відповідний розподіл вірогідності також називають стаціонарним. Знаходження стаціонарного розподілу вірогідності досягнення станів одна з основних задач теорії телетрафіка.
Теорема 2 Для ланцюга Маркова, що не приводиться і аперіодичної, завжди існує гранична вірогідність, не залежна від початкового розподілу вірогідності. Більш того, має місце одна з наступних двох можливостей: А) всі стани ланцюга неповоротні або всі поворотні нульові, і тоді вся гранична вірогідність рівна нулю і стаціонарного стану не існує; Б) всі стани поворотні ненульові і тоді існує стаціонарний розподіл вірогідності:
Стан називається ергодичним, якщо воно аперіодичне і поворотно-ненульове. Якщо всі стани ланцюга Маркова ергодичні, то весь ланцюг називається ергодичним. Граничну вірогідність ергодичного ланцюга Маркова називають вірогідністю стану рівноваги, маючи на увазі, що залежність від початкового розподілу вірогідності повністю відсутня. Ланцюг Маркова з кінцевим числом станів (кінцевий ланцюг), зручно зображати у вигляді орієнтованого графа, званого діаграмою переходів. Вершини графа асоціюються із станами, а ребра з вірогідністю переходів. Обчислення вірогідності досягнення станів проводиться прямими методами або за допомогою z-перетворення.
Ланцюг Маркова Введемо матрицю вірогідності переходів і вектор-рядок вірогідності на кроці n
Розподіл вірогідності на довільному кроці тоді підкорятиметься матричному співвідношенню:
Воно дозволяє рекурентно обчислювати всю вірогідність станів. Для знаходження граничного розподілу (стаціонарного) потрібно вирішити рівняння:
Його можна вирішувати як систему лінійних рівнянь алгебри, якщо ланцюг кінцевий. Для прикладу (мал. 1) маємо:
і рішення матричного рівняння зводиться до рішення системи трьох рівнянь:
Коефіцієнти першого рівняння в цій системі доповнюють до одиниці суму коефіцієнтів другого і третього рівнянь; це свідчить про лінійну залежність між ними. Тому для вирішення системи рівнянь потрібно ввести додаткову нормуючу умову. В даному прикладі: Вирішуючи систему отриманих рівнянь, маємо:
Рівняння для вірогідності досягнення стану в перехідному режимі вирішити значно важче. Деякого спрощення можна досягти, використовуючи z – перетворення. Застосуємо його до рівняння для перехідної вірогідності
Позначаючи відповідні перетворення, отримаємо: Всі отримані тут математичні результати відносилися до однорідних Марківських процесів, де вірогідність переходів не залежить від часу. В більш загальному випадку така залежність має місце. Розглянемо вірогідність переходу системи із стану i на m-том кроці в стан j на n-том кроці для n > m. Можна показати, що ця вірогідність зв'язана між собою, так званим рівняннями Чепмена-Колмогорова. (Chapman – Kolmogorov)
Для однорідних ланцюгів Маркова ці рівняння спрощуються оскільки
І зводяться до аналізованих вище. Завдання №1 Розробити модель роботи видавничого центру та дослідити поведінку характеристик її ефективності. У видавничому центрі є принтери для друку документів. Інтенсивність друку документів дорівнює λ документів у хв.. Середній час друку складає s хв. Передбачається, що черга документів, що очікують друкування, може бути необмеженої довжини. Параметри завдання: r = 3; λ = 0,9; s = 4 Завдання №2 Завдання № 3 Висновок У цій курсовій роботі розкриті поняття, що пояснюють функціонування системи масового обслуговування. Чітко розписані змодельовані процеси обслуговування, які дають чітке поняття про оптимізацію систем масового обслуговування. Також описані типові елементи, з яких складаються системи масового обслуговування (потік, що входить, його опис і основні особливості, черга і її дисципліна, обслуговуючі прилади і особливості механізму обслуговування, потік, що входить). Провівши дослідження СМО з кількістю каналів 3, інтенсивністю друку 0,9, і середньому часі обслуговування ми зробили висновок, що дана СМО гн є ефективною, оскільки коефіцієнт простою каналів 92,5%. Можна запропонувати внести зміни для покращення роботи СМО. А саме: зменшити кількість каналів до 1 і швидкість обслуговування до 2 хв. (поставити один принтер, більш дорогий який може друкувати з більшою швидкістю) зміни, що до інтенсивності ми вносити не можемо, отже вона залишається незмінною. Результати наших початкових досліджень наведені в таблиці, також там присутні запропоновані зміни по яким видно, що коефіцієнт простою каналів зменшився до 55%. Розглянувши таблицю нам чітко видно, що наші пропозиції доцільно застосувати, що покращить роботу СМО. Як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%. Дослідивши розроблену модель і основні показники роботи менеджера ми дійшли до висновку, що потрібно змінити вхідні параметри, щоб оптимізувати процес. За заданими параметрами ми отримали результати: Імовірність простою техніка Р0=2,04%,Коефіцієнт простою комп’ютера α=67,35%, Коефіцієнт очікування обслуговування β=47,75%,Середній час очікування Т=7,163121 хв. Розглянувши декілька варіантів внесення змін до даної СМО (приклади наведені в таблиці) ми зробили висновок, що доцільно зменшити кількість комп’ютерів до 4, що в свою чергу дасть нам збільшення простою техніка до 6,24% робочого часу, що не дуже багато, але це ж дасть нам змогу зменшити коефіцієнт простою комп’ютерів до 60,94% і коефіцієнт очікування обслуговування до 37,50%. Факт зменшення кількості комп’ютерів позитивно вплинув на процес, оскільки наші комп’ютери будуть більше працювати ніж простоювати, і відповідно утримувати 4 комп’ютери економічно вигідніше ніж 5. Якщо змінювати інтенсивність надходження вимог, то отримуємо залежність відповідно до якої збільшення інтенсивності надходження вимог призводить до погіршення роботи системи. Звідси випливає, що заданий параметр інтенсивності надходження вимог (5 вимог на годину) цілком об’єктивний і чітко підходить для оптимальної роботи системи. Як видно з результатів моделювання коефіцієнт зайнятості вузлів дорівнює 7,8%, що є явною ознакою невисокої ефективності роботи системи. Для покращення показників функціонування необхідно зменшити кількість комп’ютерів до 2 більш дорогих які дадуть змогу зменшити середній час виконання до 2 год., тоді коефіцієнт зайнятості збільшиться до 16.7% і при цьому імовірність відмови зросте лише до 4,3%.
Додаток 1
КУРСОВИЙ ПРОЕКТ з дисципліни «Моделювання систем» Допущений до захисту Виконав: «___»___________2012р. студент ІІІ курсу, групи КНСК 12 Захищений Спеціальність 6.050101 «__________________» Романчук Я.А. «___»______________2012р. Керівник проекту: Коваль Т.В. Київ-2012 Зміст Вступ 3
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.009 с.) |

 .
.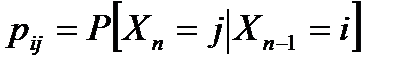 .
.

 .
.

 .
. .
.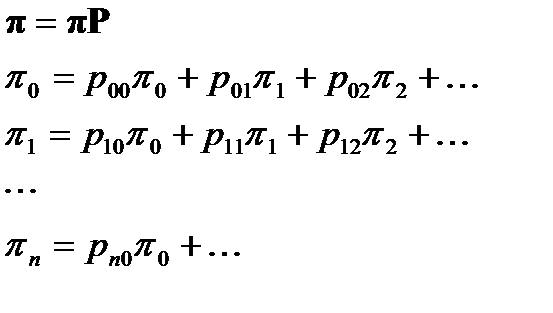
 .
.
 .
.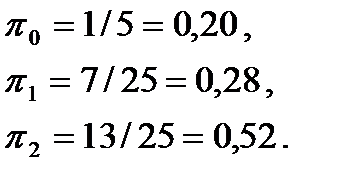
 .
. .
. .
.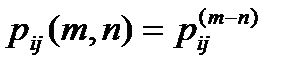 .
.


