
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет основных статистических показателейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
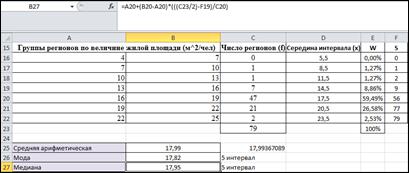
Расчет основных статистических показателей Показатели центра распределения Результаты группировки дополним следующими характеристиками: - нижняя граница интервала; - середина интервала; - верхняя граница интервала; - абсолютная частота; - относительная частота; - накопленная частота. Границы интервалов рассчитываются следующим образом: 1. Для первого интервала:
2. Для последующих интервалов:
где i = 2 … k Очевидно, что:
Нижняя граница первого интервала равна 4. Верхняя граница первого интервала равна 7. Нижняя граница второго интервала совпадает с верхней границей первого и равна 7. Верхняя граница второго интервала равна 10. Для всех последующих групп расчеты ведутся аналогично. Особенностью построения интервальных рядов является предположение об отсутствии вариации признака в пределах группы или интервала (равномерное или прямоугольное распределение). Поэтому в качестве оценки признака в группе используется середина интервала:
Абсолютные частоты – это значения в столбце «Число регионов». Относительные частоты или частости (W) – пример показателя структуры. Они определяют удельный вес единиц данной группы в составе совокупности. Как правило, выражаются в процентах. Накопленные частоты рассчитываются по формулам:
Таким образом, дополненные результаты группировки представлены в таблице 4. Таблица 4 – Дополненные результаты группировки
Первая группа показателей – показатели центра распределения: средняя, мода и медиана. Средняя рассчитывается по формуле средневзвешенной через абсолютные или относительные частоты:
или
Расчет средней арифметической представлен на рисунке 1.
Рисунок 1 – Расчет средней арифметической.
То есть средняя общая площадь жилых помещений, приходящаяся в среднем на одного жителя в 79 регионах РФ равна 17,99 м2. Модальное значение признака рассчитывается по формуле:
где xн – нижняя граница модального интервала; fMo – абсолютная частота признака в модальном интервале; fMo-1 – абсолютная частота признака в интервале, предшествующего модальному; fMo+1 – абсолютная частота признака в интервале, следующего за модальным; h – величина интервала изменения признака в группах. Первое что нужно определить, это интервал с наиболее часто повторяющимся значением (с максимальной абсолютной или относительной частотой). В данном случае это пятый интервал. Расчет моды представлен на рисунке 2.
Рисунок 2 – Расчет моды.
То есть самая распространенная общая площадь жилых помещений, приходящаяся в среднем на одного жителя в 79 регионах РФ равна 17,82 м2. Медиана рассчитывается по формуле:
где xн – нижняя граница медианного интервала; h – длина интервала; SMe-1 – накопленная частота интервала, предшествующего медианному; fMe – абсолютная частота медианного интервала. Первоначально нужно определить интервал, в котором накапливается не менее половины всей совокупности, то есть:
Половина совокупности равна 39,5 (79/2). Очевидно, что медианный интервал пятый. Расчет медианы представлен на рисунке 3.
Рисунок 3 – Расчет медианы.
То есть в 79 регионах РФ величина общей площади жилых помещений, приходящаяся в среднем на одного жителя не превышала 17,95 м2. Показатели структуры распределения Нижний (первый) квартиль рассчитывается по формуле:
где xн – нижняя граница квартильного интервала; h – длина интервала; SQ1-1 – накопленная частота интервала, предшествующего квартильному; fQ1 – абсолютная частота квартильного интервала. Первоначально нужно определить интервал, в котором накапливается не менее четверти всей совокупности, то есть:
Аналогично рассчитывается верхний (третий) квартиль по формуле:
Первый квартиль находится в пятом интервале, а третий квартиль – в шестом: 1/4 от 79 = 19,75 3/4 от 79 = 59,25 Расчет верхнего и нижнего квартиля представлен на рисунке 4.
Рисунок 4 – Расчет верхнего и нижнего квартиля.
Показатели вариации Наиболее простым является расчет показателя размаха вариации R как разницы между максимальным (xmax) и минимальным (xmin) наблюдаемыми значениями признака:
R = 25-4 = 21 То есть в 79 регионах РФ общая площадь жилых помещений, приходящаяся в среднем на одного жителя, варьируется в пределах от 4 до 25. Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Точнее характеризует вариацию признака показатель, основанный на учете колеблемости всех значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений отдельных единиц признака от средней величины. Простейший показатель такого типа – среднее линейное отклонение или среднее абсолютное отклонение как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
или
Для расчета среднего линейного отклонения используется функция =ABS(). Расчет представлен на рисунке 5.
Рисунок 5 – Расчет среднего линейного отклонения.
Дисперсия для сгруппированных данных рассчитывается по формуле:
или
Расчет дисперсии представлен на рисунке 6.
Рисунок 6 – Расчет дисперсии.
Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии и показывает, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности:
расчет основных статистических показателей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.30 (0.006 с.) |











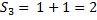 и т.д.
и т.д.



 ,
,
 =17,82
=17,82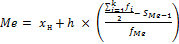 ,
,
 = 17,95
= 17,95 ,
, ,
,

 = 16,69
= 16,69 = 19,46
= 19,46



 = 1,61
= 1,61


 = 5,34
= 5,34




