Проверка адекватности обучения

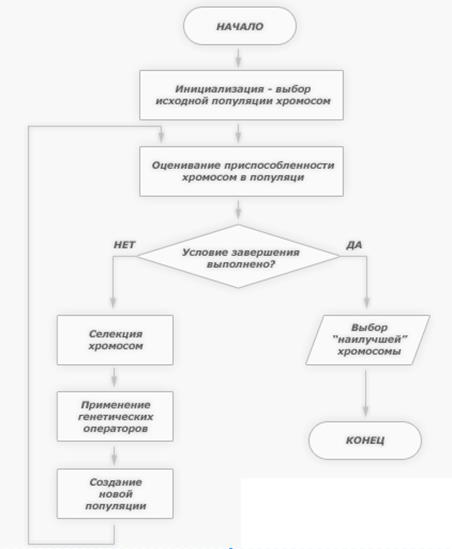
Даже в случае успешного, на первый взгляд, обучения сеть не всегда обучается именно тому, чего от неё хотел создатель.[2]

Вывод

В алгоритме обучения ничего не говорится о том, насколько будет продолжительным во времени процесс обучения сети. В некоторых ситуациях бывает очень трудно определить выполнено ли условие разделимости для обучающего множества. Так же в некоторых примерах простой перебор всех возможных весов может оказаться лучше. Эти проблемы являются важной областью современных исследований.

Генетический алгоритм

Генети́ческий алгори́тм (англ. genetic algorithm) ‒ это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.

Описание алгоритма:

Схема работы генетического алгоритма:

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

 

Некоторым, обычно случайным, образом создаётся множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определённое значение («приспособленность»), которое определяет насколько хорошо фенотип им описываемый решает поставленную задачу.

Из полученного множества решений («поколения») с учётом значения «приспособленности» выбираются решения (обычно лучшие особи имеют большую вероятность быть выбранными), к которым применяются «генетические операторы» (в большинстве случаев «скрещивание» ‒ crossover и «мутация» ‒ mutation), результатом чего является получение новых решений. Для них также вычисляется значение приспособленности, и затем производится отбор («селекция») лучших решений в следующее поколение.[3]

 

 

Этот набор действий повторяется итеративно, так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:

• нахождение глобального, либо субоптимального решения;
• исчерпание числа поколений, отпущенных на эволюцию;
• исчерпание времени, отпущенного на эволюцию.

Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

§ Задать целевую функцию (приспособленности) для особей популяции;

§ Создать начальную популяцию (Начало цикла);

§ Размножение (скрещивание);

§ Мутирование;

§ Вычислить значение целевой функции для всех особей;

§ Формирование нового поколения (селекция);

§ Если выполняются условия останова, то (конец цикла), иначе (начало цикла);

§ Создание начальной популяции;

Перед первым шагом нужно случайным образом создать начальную популяцию; даже если она окажется совершенно неконкурентоспособной, генетический алгоритм все равно достаточно быстро переведет ее в жизнеспособную популяцию. Таким образом, на первом шаге можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции, и на них можно было подсчитать функцию приспособленности (Fitness). Итогом первого шага является популяция H, состоящая из N особей.

Размножение (Скрещивание)

Размножение в генетических алгоритмах обычно половое ‒ чтобы произвести потомка, нужны несколько родителей, обычно два.

Размножение в разных алгоритмах определяется по-разному ‒ оно, конечно, зависит от представления данных. Главное требование к размножению ‒ чтобы потомок или потомки имели возможность унаследовать черты обоих родителей, «смешав» их каким-либо способом.

Почему особи для размножения обычно выбираются из всей популяции H, а не из выживших на первом шаге элементов H0 (хотя последний вариант тоже имеет право на существование)? Дело в том, что главный бич многих генетических алгоритмов ‒ недостаток разнообразия (diversity) в особях. Достаточно быстро выделяется один ‒ единственный генотип, который представляет собой локальный максимум, а затем все элементы популяции проигрывают ему отбор, и вся популяция «забивается» копиями этой особи. Есть разные способы борьбы с таким нежелательным эффектом; один из них ‒ выбор для размножения не самых приспособленных, но вообще всех особей.

 

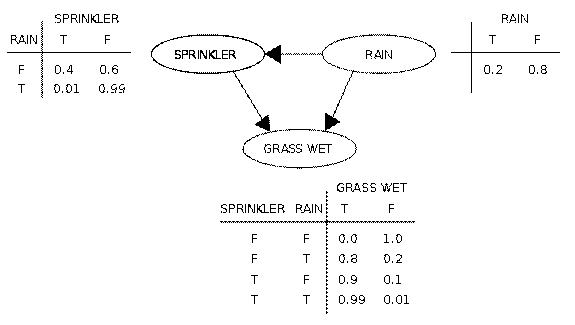
Мутации

К мутациям относится все то же самое, что и к размножению: есть некоторая доля мутантов m, являющаяся параметром генетического алгоритма, и на шаге мутаций нужно выбрать mN особей, а затем изменить их в соответствии с заранее определенными операциями мутации.

Отбор

На этапе отбора нужно из всей популяции выбрать определенную ее долю, которая останется «в живых» на этом этапе эволюции. Есть разные способы проводить отбор. Вероятность выживания особи h должна зависеть от значения функции приспособленности Fitness(h). Сама доля выживших s обычно является параметром генетического алгоритма, и ее просто задают заранее. По итогам отбора из N особей популяции H должны остаться sN особей, которые войдут в итоговую популяцию H'. Остальные особи погибают.[4]

Вывод

Генетические алгоритмы в разных формах применяются к решению многих научных и технических проблем. Генетические алгоритмы используются при создании других вычислительных структур, например, автоматов или сетей сортировки. В машинном обучении они используются при управлении роботами. Они также применяются при моделировании развития в разных предметных областях. Генетические алгоритмы являются эффективной процедурой поиска, которая конкурирует с другими процедурами. Эффективность генетических алгоритмов сильно зависит от таких деталей, как метод кодирования решений, операторов, настраивания параметров, отдельных критериев успеха.

Байесовская сеть

Байесовская сеть (или Байесовская сеть доверия) ‒ это вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей. Например, байесовская сеть может быть использована для вычисления вероятности того, чем болен пациент по наличию или отсутствию ряда симптомов, основываясь на данных о зависимости между симптомами и болезнями.

Формально, байесовская сеть ‒ это направленный ациклический граф, вершины которого представляют переменные, а ребра кодируют условные зависимости между переменными. Вершины могут представлять переменные любых типов, быть взвешенными параметрами, скрытыми переменными или гипотезами. Существуют эффективные методы, которые используются для вычислений и обучения байесовских сетей. Байесовские сети, которые моделируют последовательности переменных, называют динамическими байесовскими сетями. Байесовские сети, в которых могут присутствовать как дискретные переменные, так и непрерывные, называются гибридными байесовскими сетями.

Предположим, что может быть две причины, по которым трава может стать мокрой (GRASS WET): сработала дождевальная установка, либо прошел дождь. Также предположим, что дождь влияет на работу дождевальной машины (во время дождя установка не включается). Тогда ситуация может быть смоделирована проиллюстрированной Байесовской сетью. Все три переменные могут принимать два возможных значения: T (правда ‒ true) и F (ложь ‒ false).

Совместная вероятность функции:

P(G,S,R) = P(G | S,R)P(S | R)P(R), где имена трех переменных означают G = Трава мокрая (Grass wet), S = Дождевальная установка (Sprinkler), и R = Дождь (Rain).

Модель может ответить на такие вопросы как «Какова вероятность того, что прошел дождь, если трава мокрая?» используя формулу условной вероятности и суммируя переменные:

Вывод:

В силу того, что Байесовская сеть ‒ это полная модель для переменных и их отношений, она может быть использована для того, чтобы давать ответы на вероятностные вопросы. Например, сеть можно использовать чтобы получить новое знание о состоянии подмножества переменных наблюдая за другими переменными (переменные ‒ свидетельства). Это процесс вычисления апостериорного распределения переменных по переменным-свидетельствам называют вероятностным выводом. Это следствие дает нам универсальную оценку для приложений, где нужно выбрать значения подмножества переменных, которое минимизирует функцию потерь, например вероятность ошибочного решения. Байесовская сеть может также считаться механизмом для автоматического построения расширения Теоремы Байеса для более сложных задач.

 

 

Интеллектуальные САПР