Определение ширины запрещенной зоны полупроводника

 

Поскольку подвижность электронов и дырок слабо зависит от температуры формулу (26) мы можем записать в виде:

 

, (27)

 

где DE_g – ширина запрещенной зоны; k – постоянная Больцмана; Т – температура по шкале Кельвина; s(T) – удельная электропроводность кристалла как функция температуры, s₀ - начальная удельная электропроводность.

На эксперименте определяется сопротивление образца R. Величина, обратная сопротивлению образца, называется электропроводностью: Σ=1/ R. При этом удельная электропроводность σ и сопротивление образца связаны соотношением:

 

,

 

где S -площадь поперечного сечения образца, l - его длина. Отношение S/l изменяется незначительно при изменении температуры, поэтому σ и отличаются постоянным множителем, не зависящим от температуры и в формуле (27) вместо удельной электропроводности σ можно использовать :

 

, (28)

 

где - начальное сопротивление.

Взяв натуральный логарифм от левой и правой частей (28), получим:

 

. (29)

 

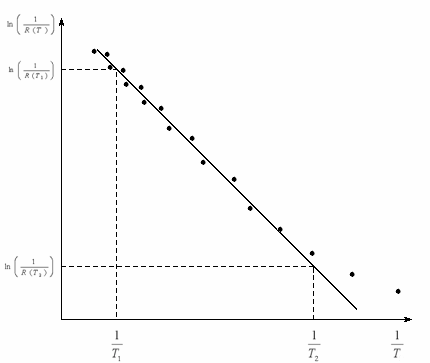
График функции от в области собственной проводимости представляет собой прямую линию (рис. 12). Тангенс угла между данной прямой и осью абсцисс равен DE_{g .}/(2k). На этом и основан экспериментальный метод определения ширины запрещенной зоны полупроводников по измерению проводимости (сопротивления).

Формула для расчета ширины запрещенной зоны на основании графика, представленного на рис. 12, имеет следующий вид:

 

(30)

 

 

Рис 12. Зависимость натурального логарифма обратного сопротивления полупроводника от обратной температуры.

 

Точки 1 и 2 берутся на прямой (см. ниже). Для удобства расчета формулу (30) представим в виде:

 

(31)

 

где tgα определяется по формуле:

 

(32)

 

Величину tgα невозможно определить из графика путем измерения угла на графике и вычисления тангенса этого угла, так как в данном случае tgα - величина, размерность которой равна градусу Кельвина. Для определения значения этой величины вначале наносят экспериментальные точки. Далее проводится усредняющая прямая, наилучшим образом согласующаяся с этими точками в той области температур, где собственная проводимость значительно превышает примесную (50 ─ 100⁰С). При расчетах на компьютере используется метод наименьших квадратов. На усредняющей прямой берутся точки 1 и 2 (см. рис. 12). Для этих точек определяются значения величин ln[1/ R(T) ] и , которые и подставляются в формулу (32).

 

Определение температурного коэффициента сопротивления металла

 

Сопротивление металла при температурах от 0^оС и выше определяется по широко известной формуле:

 

, (33).

 

где - температура по шкале Цельсия, - сопротивление при =0^оС. Она легко получается, если использовать выражение для удельного сопротивления (23). Если известны сопротивления и при температурах и , соответственно, то температурный коэффициент сопротивления металла определится по формуле:

(34)

 

Для определения используется график зависимости сопротивления от температуры (рис. 13).

 

 

Рис. 13. Зависимость сопротивления металла от температуры

 

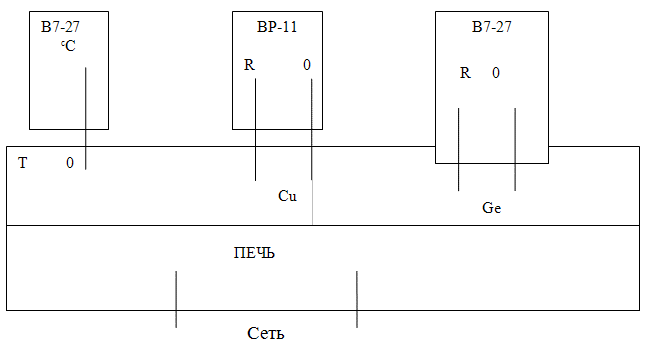
Вначале на график наносятся экспериментальные данные. Далее проводится усредняющая прямая, на которой выбираются точки 1 и 2, которые должны заметно отстоять друг от друга. Для определения прямую продолжают до пересечения с осью ординат, которой соответствует = 0^оС.

Блок-схема установки приведена на рис. 13. Нагревательная печь (сушильный шкаф) питается от сети переменного тока 220 В. В печи находятся исследуемые объекты – монокристалл германия и катушка медного провода. Их сопротивления определяются с помощью электронных вольтметров, работающих в режиме измерения сопротивлений. Температура измеряется с помощью специального датчика, присоединяемого к вольтметру.

 

Рис.13. Блок-схема установки

Задание

 

1. Измерить зависимость сопротивления меди и германия от температуры. Измерения сопротивления проводить через каждые 5^оС в области от комнатной температуры до 100^оС. Полученные результаты занести в таблицу 1. На основании данных таблицы 1 построить графики зависимостей R_Cu(T^oC) и R_Ge(T^oC).

Таблица 1

 

T^oC	RCu, кОм	RGe, кОм

 

2. Определить ширину запрещенной зоны германия, для чего:

2.1 Заполнить таблицу 2. В расчетных данных для Ln(1/R_Ge) и 1/T приводить три значащих цифры.

2.2 По данным таблицы 2 построить график зависимости Ln(1/R_Ge) от (), аналогичный тому, который представлен на рис. 12.

2.3 Для данных, соответствующих области 50-100⁰С, провести на графике усредненную прямую.

2.4 Выбрать на прямой точки 1 и 2 и определить координаты этих точек.

2.5 Определить тангенс угла наклона прямой по формуле (32).

2.6 Рассчитать ширину запрещенной зоны германия по формуле (31). Постоянная Больцмана k = 1,38∙10^-23 Дж/K

3. Определить температурный коэффициент сопротивления меди, для чего:

3.1 Построить график зависимости сопротивления катушки из медной проволоки от температуры по шкале Цельсия. За начало оси температур принять = 0^оС.

3.2 Провести усредняющую прямую.

3.3 Выбрать на прямой точки 1 и 2 и определить величины , , , .

3.4 Продолжить усредняющую прямую до пересечения с осью ординат и определить величину .

3.5 Провести расчет по формуле (34).

 

Таблица 2

 

T^oC	T, K	1/T, K^-1 (3 знача- щих цифры)	RCu, кОм	1/RGe, (кОм)^-1	Ln(1/RGe) (3 знача- щих цифры)

Контрольные вопросы

 

1. Сформулируйте основные положения, лежащие в основе классической теории электропроводности.

2. Получите формулу для плотности тока. Какие величины определяют удельное сопротивление?

3. Что такое средняя длина свободного пробега электрона и подвижность?

4. Как зависит от температуры удельное сопротивление металлов?

5. Что такое валентная зона, запрещённая зона и зона проводимости?

6. Что такое металлы, полупроводники и диэлектрики с точки зрения зонной теории?

7. Какие электроны дают вклад в электропроводность, теплопроводность и теплоёмкость металлов?

8. Как зависит от температуры концентрация носителей заряда в собственном и примесном полупроводниках?

Литература

 

1. Савельев И.В. Курс общей физики, т. 2. – М.: КНОРУС, 2012, с. 262 – 272.

2. Савельев И.В. Курс общей физики, т.3. – М.: КНОРУС, 2012, с. 213 –. 245

3. Наркевич И.И. Физика: Учеб./ И.И. Наркевич, Э.И. Волмянский, С.И. Лобко. – Мн.: Новое знание, 2004, с. 320 – 325, 563 – 581.

4. Трофимова Т.И.Курс физики: учеб. пособие для вузов./ Т.И. Трофимова. – М.: «Академия», 2007, с. 186 – 191, 441 – 459.