Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание лабораторного занятия № 19Содержание книги Поиск на нашем сайте
«Измерение длины волны при помощи дифракционной решетки» (наименование лабораторного занятия) по дисциплине «ФИЗИКА» (наименование дисциплины) Цель занятия: изучить свойства света как электромагнитной волны и определять ее характеристики». Оборудование: проекционный фонарь, дифракционная решетка, экран с миллиметровым масштабом, измерительная линейка, набор светофильтров, разрядная газоразрядная трубка (неон или азот), индукционная катушка. λ = необходимо знать
 tg tg   (из рисунка) (из рисунка)  Подставляя значение  в выражение (1), получим окончательную формулу для нахождения длины волны: λ = в выражение (1), получим окончательную формулу для нахождения длины волны: λ =  (2) (2)
Длины волн измеряются в нанометрах (1 нм = 10-9 м). Ход работы. 1. Включить лампочку проекционного фонаря в сеть переменного тока.
8. Между дифракционной решеткой и проекционным фонарем поставить различные светофильтры и пронаблюдать дифракционный спектр от монохроматического света. 9. Вычислить погрешность измерений, ответ записать в виде λ= λср+ ∆λср Контрольные вопросы. 1. Почему дифракционная картина, полученная в белом свете спектральная? 2. Какому из цветов(фиолетовому, красному) соответствует больший угол отклонения? 3. Зависит ли положение максимумов освещенности, создаваемых дифракционной решеткой, от числа щелей?
Министерство образования и науки Краснодарского края
Государственное БЮДЖЕТНОЕ образовательное учреждение среднего профессионального образования
«Новороссийский колледж радиоэлектронного приборостроения» КРАСНОДАРСКОГО КРАЯ
Описание лабораторной работы № 20
«Изучение свойств элементарных частиц По фотографиям треков» по дисциплине «ФИЗИКА» (наименование дисциплины) Цель занятия: научиться определять частицы и их параметры по фотографиям треков. Оборудование: 1. Фотографии косых столкновений частиц, транспортир, линейка, тонко отточенный карандаш. Теоретическая часть. В результате нецентрального (косого) соударения двух элементарных частиц каждая разлетается по траектории, выходящей из одной точки, поэтому образуется «вилка».
такого взаимодействия движущейся частицы (масса её M, скорость движения до и после взаимодействия v и v 1) и неподвижной (масса её m, скорость движения после Рис. 1 взаимодействия u). θ – угол рассеяния; φ – угол отдачи; Mv и Mv1 – векторы импульсов налетающей частицы до и после взаимодействия; mu – вектор импульса неподвижной частицы после взаимодействия. Энергия частиц до взаимодействия Mv2/2 после взаимодействия Mv12/2 и Mu2/2, поэтому в соответствии с законом сохранения энергии запишем уравнение Mv2/2 = Mv12/2 + Mu2/2 (1) Из ∆AOC (рис.1), согласно теореме синусов, запишем Mu/sin θ = Mv/sin(π-(θ+φ)); Mv1/sin φ = Mv/sin(π-(θ+φ)). Следовательно, u = Mv sin θ/ sin(mπ-(θ+φ) (2) v1=v sinφ/ sin(θ+φ), Уравнения (2) подставим в уравнение (1), и получим
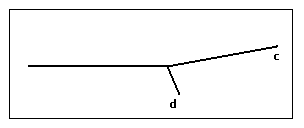
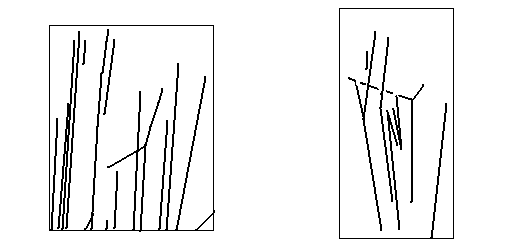
После сокращения обеих частей последнего уравнения на Mv2/2 Имеем или Преобразуем левую часть уравнения (3), зная, что sin2α+sin2β=sin (α + β) sin (α - β); sin2 (θ+φ) –sin2φ=sin(θ+2φ) sinθ. Следовательно, sin2 (θ+φ) –sin2φ=sin(θ+2φ) sinθ.(4) Учитывая выражение (4), уравнение (3) запишем так: sin(θ+2φ) sinθ=Msin2θ/m или M/m=sin (θ+2φ)/sinθ. (5) Исследуя треки заряженных частиц по готовым фотографиям и используя формулу (5), можно решить ряд задач. На фотографии треков частиц в толстослойной эмульсии (рис. 2) след с – трек рассеянной частицы. Зная, что d- трек протона, определить неизвестную частицу.
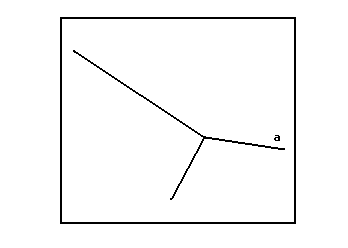
(Рис. 2) Ход работы. 1. Используя рис. 1, начертить в тетради трек налетающей частицы и продолжить его. 2. Начертить прямолинейные участки треков взаимодействующих частиц, сохранив углы рассеяния θ и отдачи φ. Отметить эти углы. 3. Записать массу m известной частицы в а.е.м. и, используя формулу (5), вычислить массу M рассеянной частицы. 4. Зная М, используя таблицу «Периодическая система элементов», определить, ядром какого атома является рассеянная частица. Назовите частицу. 5. Результаты измерений, вычислить и записать в таблицу. 6. Исследование повторить (п. 1-6) для решения задачи II. Сталкиваясь в камере Вильсона с атомом газа, α-частица отклонилась на 142º. Определить, с атомом какого газа столкнулась α-частица (рис. 3)
Контрольные вопросы. 1. Назовите формулу кинетической энергии частиц; сформулируйте закон сохранения энергии.
Рис. 3 Рис. 4
Рис. 5
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.104.30 (0.01 с.) |

 (1)
(1) и тогда
и тогда

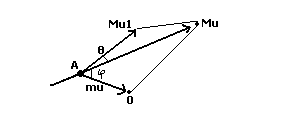 На рис 1. Показана импульсная диаграмма
На рис 1. Показана импульсная диаграмма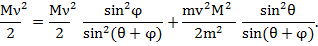
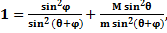
 (3)
(3)