Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: моделювання кола постійного та синусоідального струму засобами MatlabСодержание книги
Поиск на нашем сайте Мета: Отримати практичні навички моделювання кіл постійного та синусоїдального струму засобами Matlab
Для схеми розробити алгоритм і скласти програму що передбачає: • Розрахунок струмів у гілках методом контурних токів • Перевірку балансу потужностей. • Побудування потенційної діаграми для будь-якого замкненого контуру, що включає джерело ЕРС. Зробити перевірочний розрахунок: • Промоделювати процеси в електричній схемі в середовищі Simulink (бібліотека PowerSystemBlockset). Систему лінійних рівнянь з невідомими струмами, розв'язати методом Крамера. Для цього створити універсальну власну функцію за відповідним алгоритмом.
Струм контуру помножується на суму опорів контуру, потім опір, який належить двом контурам помножується на струм контуру, сполученого з даним контуром і знак визначається за напрямком контурних струмів. II(r1+r5+r6+r7)-IIIr5-IIII(r6+r7)=-J1(r5+r6+r7) -IIr5+III(r2+r4+r5)-IIIIr2=E2+J1r5 -II(r6+r7)-IIIr2+IIII(r2+r3+r6+r7)=-E2+J1(r5+r6+r7) Якщо в контурі присутня ЕРС вона записується в правій частині рівняння як за 2-им законом Кірхгофа. Гілка з джерелом струму виділяється як гілка зв’язку. Ця гілка входить тільки до одного контуру і його контурний струм дорівнює струму джерела струму. Для цього контуру складати рівняння не треба, але для інших контурів цей струм треба враховувати.Потім струми в гілках електричної схеми обчислюються за допомогою обчислених контурних струмів. I1=ІІ I2=III-IIIII5=IIІ-II-J1 I4=IІІI3=IIIII6=I2-I5 Перевірка балансу потужностей Перевірка балансу потужностей необхідна для перевірки результатів обчислення струмів гілок електричної схеми. Для роботи схеми у нормальному режимі, необхідно щоб потужність, яка генерується джерелами живлення схеми, дорівнювала потужності споживачем.
де Е – ЕРС Ik– струм джерела струму; Uk – напруга на джерелі струму; І – струми гілок; R – відповідні опори гілок; Баланс потужностей не повинен перевищувати 5 %. В нашому випадку:
Побудування потенціальної діаграми для контуру, який має ЕРС Потенціальна діаграма є однією з перевірок струмів у схемі. При обходу якого-небудь замкненого контуру потенціал вузла, з якого починається обхід, приймаємо рівним нулю, і якщо після закінчення обходу останній потенціал (тобто потенціал з якого починали обхід) дорівнює нулю, то струми в контурі розраховані правильно. Для побудови потенціальної діаграми φ(R) треба розрахувати вектор потенціалів і відповідний до нього вектор опорів. v=[0 I(4)*R(4) I(2)*R(2)-E(2)+I(4)*R(4)I(5)*R(5)-E(2)+I(2)*R(2)+I(4)*R(4)] r0=[0 R(4)R(4)+R(2)R(4)+R(2)+R(5)] Для обчислення струмів та напруг у електричних колах матричним методом спершу необхідно визначити наступні параметри: q – кількість вузлів у схемі; m=q-1 – кількість незалежних вузлів; р – кількість гілок з невідомими струмами; n=p-m– кількість незалежних контурів. Після цього складаємо матриці незалежних контурів Gрозміром (p*n), з’єднань Dрозміром (m*p), а також вектори ЕРС Е розміром (р*1), джерел струму Jk розміром (т*1), квадратну діагональну матрицю опорів Z розміром (р*р). Елементи матриць G і D утворюються згідно з формулами: Gij=1, коли напрям і –ої гілки співпадає з напрямом j –огоконтура; -1, навпаки; 0, коли гілка і не належить контуру j. Dij=1, коли напрям j- оїгілки до вузла і; -1, навпаки; 0, коли гілка j не підходе до вузла і. А= [D; G’*Z]; B= [-Jk; G’*E], отримаємо систему лінійних рівнянь А*І=В, яку можна вирішити любим з відомих методів.
Рішення лінійних рівнянь методом Крамера Суть методу зручно зрозуміти на прикладі рішення системи двох алгебраїчних рівнянь з двома невідомими.
або у векторній формі АХ=В де А= Нехай відомо, що визначник матриці А не є нульовим. тобто detA≠0. Якщо кожне з рівнянь системи помножити відповідно на алгебраїчні доповнення ad11 iad21 потім отримані рівняння скласти, то для першого рядка отримаємо: (a11*ad11+a21*ad21)*x1+(a12*ad11+a22*ad21)*x2=b1*ad11+b2*ad21. За правилами математики: a11=ad22 a22=ad11 -a12=ad21 -a21=ad12 Тому після підстановки одержимо: (a11*a22-a12*a21)*x1+(a12*a22-a22*a12)*x2=b1*a22-b2*a12. a11*a22-a12*a21=detA (a12*a22-a22*a12)*x2=0 b1*a22-b2*a12= звідки x1= Аналогічно можна отримати формулу обчислення х2 з другого рядка. Наведені положення та формули дійсні для матриць любого розміру. Якщо визначник основної матриці А систем n лінійних алгебраїчних рівнянь з n невідомими не дорівнює нулю (detA≠0),то така система має єдине рішення, яке визначаеться за формулою xі= Наприклад B1= Матриця Ві формується шляхом заміни і-го стовпця матриці А на стовпець В.
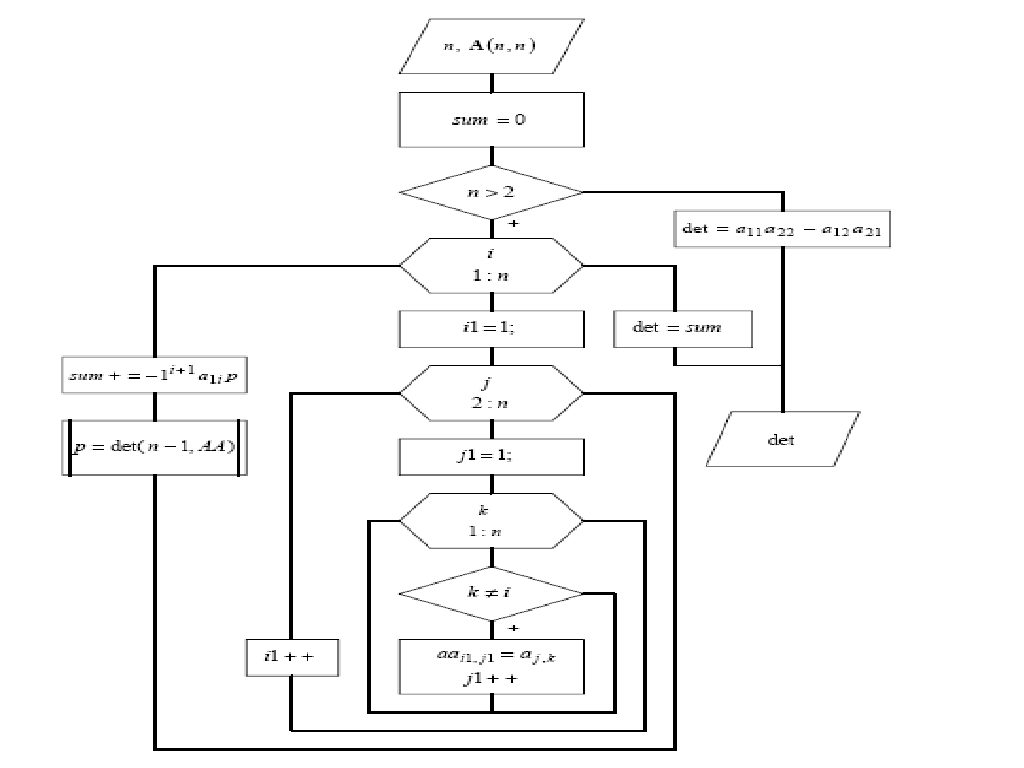
Блок-схема обчислення визначника матриці А
Блок-схема алгоритму методу Крамера
ПРОГРАМА ОБЧИСЛЕНЬ Матричний метод clc closeall %Матричный метод E2=10;ik=3 G=[1 0 0; 0 1 -1; 0 0 1; 0 1 0; -1 1 0; 1 0 -1] D=[0 -1 0 0 1 1; 1 0 -1 0 0 -1; 0 1 1 -1 0 0] E=[0 0] J=[0 0] R=[8 14 20 12 40 18] Z=diag(R); A=[D;G'*Z]; B=[-J;G'*E]; I=A\B bI=D*I+J; bU=G'*Z*I-G'*E; методконтурних струмів clc closeall r1=8;r2=14;r3=20;r4=12;r5=40;r6=12;r7=6;ik=3;E=10; A=[r1+r5+r6+r7 -r5 -(r6+r7);-r5 r2+r4+r5 -r2;-(r6+r7) -r2 r2+r3+r6+r7] B=[-ik*(r6+r7+r5);E+ik*r5;ik*(r6+r7)-E] %Метод Крамера dA=det(A) for j=1:3 Aj=A; Aj(:,j)=B; d(j)=det(Aj); end i=d/dA i1=i(1) i4=i(2) i3=i(3) i5=i4-i1-ik i2=i4-i3 i6=i2-i5 Перевiрка балансу потужностей Pist=abs(i2)*E+ik*abs(i1)*r1 Ppotr=i1^2*r1+i2^2*r2+i3^2*r3+i4^2*r4+i5^2*r5+i6^2*(r6+r7) dP=abs((Pist-Ppotr)/Pist)*100 Побудування потенційної діаграми v=[0I(4)*R(4) I(2)*R(2)+I(4)*R(4)-E2I(2)*R(2)+I(5)*R(5)+I(4)*R(4)-E2]; Ro=[0 R(4) R(4)+R(2) R(4)+R(5)+R(2)]; plot(Ro,v,'r') grid
Функцiя для метода Крамера functionx=kramer(a,b) [m,n]=size(a); z=opr(n,a); for j=1:m buf=a; fori=1:m buf(i,j)=b(i); end opr_(j)=opr(n,buf); end fori=1:m x(i)=opr_(i)/z; end Функцiя для обисленнявизначникаматрицi functionD=opr(n,a) sum=0; if n>2 fori=1:n i1=1; for j=2:n j1=1; for k=1:n if k~=i aa(i1,j1)=a(j,k); j1=j1+1; end end i1=i1+1; end p=opr(n-1,aa); sum=sum+(-1)^(i+1)*a(1,i)*p; end D=sum; else D=a(1,1)*a(2,2)-a(1,2)*a(2,1); end
моделюванняелектричноі схеми в середовищі Simulink
Рисунок 5.1- Схема зібрана за допомогоюбібліотеки PowerSystemsBlockset у Simulink, пакету MatLab. РЕЗУЛЬТАТИ ОБЧИСЛЕНЬ Методконтурних струмів A = 66 -40 -18 -40 66 -14 -18 -14 52 B = -174 i1 = -2.0600 i4 = 0.7948 i3 = 0.3471 i5 = -0.1452 i2 = 0.4478 i6 = 0.5929 Перевiркабалансупотужностi Ppotr = 53.9171 Pist = 53.9171 dP = 1.3178e-014 Матричний метод G = 1 0 0 0 1 -1 0 0 1 0 1 0 -1 1 0 1 0 -1
D = 0 -1 0 0 1 1 1 0 -1 0 0 -1 0 1 1 -1 0 0 E = J = R = 8 14 20 12 40 18 I = -2.0600 0.4478 0.3471 0.7948 -0.1452 0.5929
Simulink
Результати отримані у Simulink
Потенційна діаграма Потенціальна діаграма для контуру з джерелом ЕРС Аналіз результатів
ПРАКТИЧНЕ ЗАНЯТТЯ №14
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |



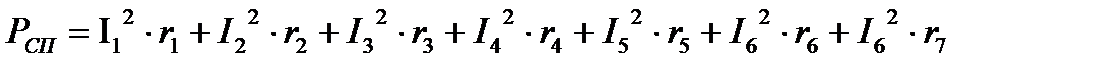
 ;
;  ;
;  ;
; 

 , В=
, В= 
 =detB1 то: detA*x1=detB1
=detB1 то: detA*x1=detB1
 , де і=1,2,3…,n.
, де і=1,2,3…,n. .
.