Законы: сохранения массы и энергии, постоянства состава, Авогадро, кратных отношений, простых объемных отношений, парциальных давлений Дальтона.

ЗСМ: Масса веществ, вступивших в реакцию, равна массе веществ, образующихся в результате реакции. ЗСЭ: При любых взаимодействиях в изолированной системе энергия этой системы остаётся постоянной. Возможны лишь переходы из одного вида энергии в другой.(E=m*c²) ЗПС: При хим. Реакциях остаётся постоянной не только общая масса веществ, но и масса каждого элемента. ЗА: В равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул. (Закон Авогадро имеет несколько следствий: Первое следствие: один моль любого газа при одинаковых условиях занимает одинаковый объём. В частности, при нормальных условиях, т. е. при 0 °C (273К) и 101,3 кПа, объём 1 моля газа, равен 22,4 л. Этот объём называют молярным объёмом газа V_m. Второе следствие: Молярная масса любого газа равна удвоенной относительной его плотности по водороду. M(x)=M(H₂)*D_H2.) ЗКО: Если два элемента образуют несколько различных соединений, то на одну и ту же массу одного из них приходятся такие массы другого, которые относятся между собой, как простые целые числа. ЗОО: при постоянном давлении и температуре объемы газов, вступающих в химическую реакцию, находятся в простых отношениях друг к другу и к объемам газообразных продуктов реакции, то есть отношение объемов, в которых газы участвуют в реакции, соответствует отношению небольших целых чисел. ЗпдД: Давление смеси газов, химически не взаимодействующих друг с другом, равно сумме парциальных давлений газов, составляющих смесь. (P_общ = P₁ + P₂ + … + P_n). Парциальное давление газа – это то давление, которое производило бы имеющееся в смеси кол-во газа, если бы оно занимало весь объём, занимаемый смесью.

 

Эквивалент элемента и вещества. Закон эквивалентов.

Эквивалент — это реальная или условная частица, которая может присоединять, высвобождать или другим способом быть эквивалентна катиону водорода в ионообменных реакциях или электрону в окислительно-восстановительных реакциях. Например, в реакции: NaOH + HCl = NaCl + H₂O эквивалентом будет реальная частица — ион Na⁺, а в реакции Zn(OH)₂ + 2HCl = ZnCl₂ + 2H₂O эквивалентом будет являться мнимая частица ½Zn(OH)_2. Под эквивалентом вещества также часто подразумевается количество эквивалентов вещества или эквивалентное количество вещества — число моль вещества, эквивалентное одному моль катионов водорода в рассматриваемой реакции. Число эквивалентности z представляет собой небольшое положительное целое число, равное числу эквивалентов некоторого вещества, содержащихся в 1 моль этого вещества. Фактор эквивалентности Э связан с числом эквивалентности z следующим соотношением: Э =1/z. Например, в реакции: Zn(OH)₂ + 2HCl = ZnCl₂ + 2H₂O Эквивалентом является частица ½Zn(OH)₂. Число ½ есть фактор эквивалентности, z в данном случае равно 2. Эквивалентная масса — это масса одного эквивалента данного вещества. Молярная масса эквивалентов вещества — масса одного моля эквивалентов, равная произведению фактора эквивалентности на молярную массу этого вещества. M_экв = Э×M, или. M_экв = M/z. Эквивалентный объём – отношение произведения молярного объёма на эквивалент элемента, к числу атомов элемента. Vэ=Vm*Э/N. В результате работ Рихтера(1792—1800) был открыт закон эквивалентов: Закон эквивалентов: все вещества реагируют и образуются в эквивалентных отношениях. m(A)/Mэкв(A)=m(B)/Mэкв(B), или V(A)/Vэкв(A)=V(B)/Vэкв(B).

Расчет молярной массы эквивалента простого и сложного вещества.

Молярная масса эквивалента простого вещества определяется как отношение молярной массы вещества к произведению числа атомов элемента в молекуле на его валентность. М_э(х) = М(х)/Z Z=N*B B – валентность

Молярная масса эквивалента оксида определяется как отношение молярной массы оксида к произведению числа атомов элемента в молекуле на его валентность. М_э(х) = М(х)/Z Z=N*B B – валентность

Молярная масса эквивалента кислоты определяется как отношение молярной массы кислоты к её основности.

Основность кислоты определяется числом ионов водорода, способных замещаться на атомы металла. М_э(х) = М(х)/Z Z=N_н+

Молярная масса эквивалента основания определяется как отношение молярной массы основания к его кислотности.

М_э(х) = М(х)/Z Z=N_он-.

Молярная масса эквивалента веществ, участвующих в ОВР – это отношение молярной массы вещества к числу электронов, отданных или принятых веществом. М_э(х) = М(х)/Z Z=N_е.

Молярная масса эквивалента иона - это отношение молярной массы иона к его заряду. М_э(х) = М(х)/Z Z – заряд иона.

5. Уравнение Менделеева-Клапейрона, основные газовые законы.

Уравнение состояния идеального газа -формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: p*Vм = R*T, гдеp — давление, Vм — молярный объём, R — универсальная газовая постоянная, T — абсолютная температура, К. Так какVм=V/n, где n — количество вещества, а n=m/M, где m — масса, M — молярная масса, уравнение состояния можно записать: p*V= n*R*T. В случае постоянной массы газа уравнение можно записать в виде: p*V/T=const. Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта (Если Т=const, то p*V=const), Шарля (Если V=const, то p/T=const) и Гей-Люссака (Если p=const, тоV/T=const). А в форме пропорции P₁*V₁/T₁=P₂*V₂/T₂ этот закон удобен для расчёта перевода газа из одного состояния в другое. Закон Авогадро: В равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул. (Закон Авогадро имеет несколько следствий: Первое следствие: один моль любого газа при одинаковых условиях занимает одинаковый объём. В частности, при нормальных условиях, т. е. при 0 °C (273К) и 101,3 кПа, объём 1 моля газа, равен 22,4 л. Этот объём называют молярным объёмом газа V_m. Второе следствие: Молярная масса любого газа равна удвоенной относительной его плотности по водороду. M(x)=M(H₂)*D_H2.). Закон парциальных давлений: Давление смеси газов, химически не взаимодействующих друг с другом, равно сумме парциальных давлений газов, составляющих смесь. (P_общ = P₁ + P₂ + … + P_n). Парциальное давление газа – это то давление, которое производило бы имеющееся в смеси кол-во газа, если бы оно занимало весь объём, занимаемый смесью.

Строение и свойства атомов

1.Квантово-механическая модель строения атома, уравнение де Бройля, принцип Гейзенберга, волновая функция, уравнение Шредингера. К сожалению, описать атомы со сложной структурой, опираясь на модель Бора, не представляется возможным. Поэтому, в 20-х годах прошлого века получила широкое распространение квантово-механическая модель (КММ) атома. В основу КММ положена квантовая теория атома, согласно которой электрон обладает как свойствами частицы, так и свойствами волны. Другими словами, о местоположении электрона в определенной точке можно судить не точно, а с определенной долей вероятности. Поэтому в КММ орбиты Бора заменили орбиталями ("электронные облака" - области пространства в которых существует вероятность пребывания электрона). Состояние электрона в атоме описывают с помощью 4 чисел, которые называют квантовыми: Главное квантовое число n (описывает Энергетический уровень орбитали, принимает значения n=1,2,3,…). Чем больше значение n, тем выше энергия электрона и больше размер электронного облака. Если в атоме несколько электронов с одинаковым n, то они образуют электронные облака одинакового размера - электронные оболочки. Орбитальное квантовое число L (Описывает форму орбитали, принимает значения от 0 до n-1). Орбитали, имеющие одинаковое n, но разные L называют энергетическими подуровнями и обозначают буквами латинского алфавита: s,p,d,f,g. Магнитное квантовое число m (Описывает ориентацию орбиталей в пространстве, принимает значения -L,0,L). Например: Для L=0 возможно только одно значение: m=0. Это значит, что s-орбиталь имеет только одну пространственную ориентацию. Для L=1: m=-1;0;+1 - p-орбиталь имеет три пространственные ориентации. Cпиновое квантовое число m_s (Описывает направление вращения электрона в магнитном поле - по часовой стрелке или против. На каждой орбитали может находиться только два электрона: один со спином +½ другой -½). Для частиц не очень высокой энергии, движущихся со скоростью v<<c (скорости свет), , где h=6,626*10^-34Дж*с – постоянная Планка. Волновая функция, или пси-функция — функция, используемая в квантовой механике для описания движения электрона в атоме. 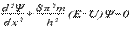² – характеризует вероятность нахождения электрона в данной точке атомного пространства и определяется с помощью уравнения Шрёдингера , де x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы. В 1927г. Гейзенберг постулировал принцип неопределённости, согласно которому положение и импульс движения субатомной частицы принципиально невозможно определить в любой момент времени с абсолютной точностью. В каждый момент времени можно определить только лишь одно из этих свойств.