
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временные параметры сетевых графиков и их нахождение.
Параметры событий:
если j имеет несколько предыдущих событий, то
где Если
Резерв времени определяется как
Показывает на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличение срока выполнения комплекса работ. Замечания. Критические события резервов времени не имеют. Отсюда вывод: определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути, в выявляя событие с нулевыми резервами времени, определяем его топологию.
       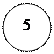 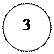  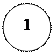   Пример: критические события Пример: критические события
1, 2, 3, 5, 6 критический путь 1→2→3→5→6 tкр = 5 + 1 + 8 + 6 = 20
Параметры работ Ранний срок начала работы
Тогда ранний срок окончания работ
Поздний срок окончания работ Очевидно
Значит поздний срок начала работ
Резерв времени пути определяется как разность между длиной критического и рассматриваемого пути
Он показывает, на сколько в сумме могут быть увеличены продолжительность всех работ, принадлежащих этому пути. Вывод: любая из работ пути Среди резервов времени выделяют 4 разновидности резервов. а) полный резерв времени
Полный резерв времени равен резерву максимальному из путей, проходящих через данную работу.
Важным свойством б) частный резерв времени 1-го вида
или Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное событие совершаются в свои самые поздние сроки. в) частный резерв 2-го вида
или Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события совершаются в свои самые ранние сроки. г) Независимый резерв времени Rн(i,j). Это часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки.
или Таким образом, если частичный резерв времени 1-го вида может быть использован на увеличение продолжительности данной и последующих работ без затрат резерва времени предшествующих работ, свободный резерв времени – на увеличение продолжительности данной и предшествующих работ без нарушения резерва времени последующих работ, то независимый резерв времени может быть использован для увеличения продолжительности только данной работы. Работы, лежащие на критическом пути, так же как и критические события, резервов времени не имеют. Если на критическом пути лежит начальное событие i, то
Если на критическом пути лежит конечное событие, то
Если на критическом пути лежит начальное и конечное событие i и j, но сама работа не принадлежит этому пути, то
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.254 (0.008 с.) |
 - определяется продолжительностью максимального пути, предшествующего этому событию.
- определяется продолжительностью максимального пути, предшествующего этому событию. (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) - любой путь, следующий за
- любой путь, следующий за 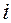 -м событием, т.е. путь от
-м событием, т.е. путь от  , то удобно пользоваться формулой
, то удобно пользоваться формулой (2.4)
(2.4) (2.5)
(2.5)
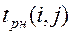 . Очевидно
. Очевидно (2.6)
(2.6)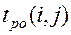
 (2.7)
(2.7)
 (2.8)
(2.8)
 (2.9)
(2.9) (2.10)
(2.10) на его участке, не совпадающем с критическим путем обладает резервом времени.
на его участке, не совпадающем с критическим путем обладает резервом времени.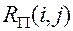 работы
работы  – показывает насколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменяется
– показывает насколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменяется (2.11)
(2.11)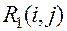 есть часть полного резерва времени, на который можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события
есть часть полного резерва времени, на который можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события (2.12)
(2.12) (2.13)
(2.13) или свободный резерв представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события.
или свободный резерв представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20)


