
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типового расчета по дисицплине «теорияСодержание книги
Поиск на нашем сайте
СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ» Методические указания предназначены для выполнения типового расчета по курсу «Теория систем и системный анализ». Содержат задания по основным задачам системного анализа: задачи управления запасами, задачи упорядочения, сетевому моделированию, принятию решений в конфликтных ситуациях (теория игр) и балансовым моделям. В первой части содержатся примеры выполнения задания по каждому из разделов, во второй – задания для самостоятельного выполнения.
Раздел I. Примеры выполнения заданий и методические указания 1. З адачи управления запасами. В данном курсе для студентов специальности 080801 в качестве примера задач системного анализа рассматриваются простейшие задачи управления запасами: а) однопродуктовая модель простейшего типа; б) модель с равномерным пополнением запаса; в) модель управления запасами с дефицитом. а) однопродуктовая модель простейшего типа: Оптимальное строение модели предусматривает заказ Оптимальное значение размера заказа (формула Вильсона)
Оптимальные затраты
Стратегия размещения заказов должна определить т. возобновления заказа. На практике это реализуется путем непрерывного контроля уровня запаса до момента достижения им очередной т. возобновления заказа.
б) модели с равномерным исполнением запаса Оптимальное значение размера заказа в этом случае равно
в) модели с дефицитом Пусть в рассматриваемой модели допускается дефицит. Пусть
Нетрудно показать, что если модель с равномерным пополнением запаса допускает дефицит, то формулы (1.4), (1.5) и (1.6) преобразуются в формулы (модель «смешанного типа»)
Пример: Ежедневный спрос на некоторый товар составляет около 100 ед. Затраты на размещение каждого запаса постоянны и равны 100 руб. Ежедневные затраты на хранение ед. запаса составляют 0,02 руб. Нужно определить экономический размер партии и точку возобновления заказа при сроке выполнения заказа, равном 12 дням. Решение:
Соответствующая оптимальная продолжительность составляет
Заказ размером Усложним условия задачи. Пусть запасы пополняются равномерно с интенсивностью Тогда
Еще раз скорректируем условие задачи. Пусть в первоначальной модели допускается дефицит. Причем удельные потери от дефицита составляют
Задачи упорядочения. Характеризуются следующими особенностями. Например, имеется множество различных деталей с определенными технологическими маршрутами, а также несколько единиц оборудования (фрезерный, токарный, шлифовальный станки), на которых эти детали обрабатываются, т.к. одновременно обрабатывать более одной детали невозможно, у некоторых станков может образоваться очередь, т.е. деталей, ждущих обработки. Время обработки каждой детали известно. Определить такую очередность обработки деталей на каждом станке, при котором минимизируется некоторый критерий оптимальности, например, суммарная продолжительность завершения комплекса работ. Также задача называется задачей календарного планирования или составления расписания, а выбор очередности запуска деталей в обработку – упорядочением. В качестве примера рассмотрим упрощенный вариант этой задачи, для которой разработан удобный алгоритм. Пусть имеется несколько изделий, каждое из которых должно быть обработано на 2-х машинах (станках). Известны время обработки и последовательность обработки каждого изделия на каждой машине. Требуется выбрать такой порядок обработки изделий, при котором суммарное время обработки будет минимальным. Основные ограничения: а) время перехода от одной машины к другой незначительно и им можно пренебречь; б) каждое изделие обрабатывается в определенном технологическом порядке; в) каждое обслуживание должно быть завершено прежде, чем начнется следующее. Обозначим Пример:
Построение модели. Пусть
Так как сумма Построение алгоритма. Для нахождения оптимальной последовательности порядка обслуживания “m” требований на 2-х пунктах обслуживания наибольшую известность получил «алгоритм Джонсона». Включает следующие этапы: а) поиск наименьшего элемента: Рассмотрим все б) перестановка изделий: Если выбранная величина находится в 1-й строке (относится к 1-й машине), то соответствующее изделие помещается на обслуживание в первую возможную очередь. Если – во 2-й строке (относится ко 2-й машине) – то в последнюю очередь. в) исключение из рассматриваемого выбранного изделия: Выбранному изделию присваивается новый номер в очереди, который в дальнейшем считается занятым. Из последующего рассмотрения оно исключается. Далее осуществляется переход к этапу а). После определения оптимального порядка обработки изделий на машинах графически определяется время простоя и работы 2-й машины, которое является минимальным из всех возможных.
Сетевое моделирование. Порядок и правила построения сетевых графиков: 1) Сеть строится слева направо, от исходного события к завершающему. 2) Длина и наклон стрелок значения не имеют. Однако все они направлены слева направо. 3) В сети не должно быть контуров (т.е. замкнутых путей). 4) Сетевой график – это плоский график, поэтому стрелки в нем не должны пересекаться.
6) В сети не должно быть (кроме исходного) хвостовых событий, т.е. событий, в которые не входит ни одна работа. 7) В сети не должно быть (кроме завершающего) тупиковых событий, т.е. событий, из которых не выходит ни одна работа. Нумерация (упорядочение сетевого графика) производится по методу ранжирования. Пример:
3,4 – событие 2-го ранка; 5 – событие 3-го ранга.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.007 с.) |

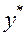 ед. продукции через каждые
ед. продукции через каждые 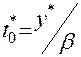 ед. времени.
ед. времени.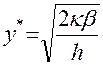 (1.1)
(1.1)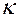 - затраты на оформление заказа;
- затраты на оформление заказа; - интенсивность спроса.
- интенсивность спроса. (1.2)
(1.2) - затраты на хранение в ед. времени.
- затраты на хранение в ед. времени. (1.3)
(1.3) (1.4)
(1.4)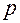 - удельные потери от дефицита. Тогда можно показать (6), что оптимальное значение размера заказа для данных случаев
- удельные потери от дефицита. Тогда можно показать (6), что оптимальное значение размера заказа для данных случаев (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8)

 размещается, когда уровень запаса достигает
размещается, когда уровень запаса достигает 



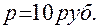 Тогда
Тогда
 - величина дефицита.
- величина дефицита. - время обработки j-го изделия на 1-й машине,
- время обработки j-го изделия на 1-й машине,  - на 2-й машине.
- на 2-й машине.





























 - время простоя 2-й машины между концом выполнения работы по обработке
- время простоя 2-й машины между концом выполнения работы по обработке  -го изделия на 2-й машине и началом обработки
-го изделия на 2-й машине и началом обработки  -го изделия на той же самой машине. Тогда суммарное время обработки изделий составит:
-го изделия на той же самой машине. Тогда суммарное время обработки изделий составит:
 известна, то надлежит минимизировать
известна, то надлежит минимизировать 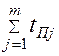 (в нашем случае
(в нашем случае 
 и
и  . В нашем случае это
. В нашем случае это  .
.
















 n1=4
n1=4
 Тmin=23+4+1=34
Тmin=23+4+1=34 5) Пара событий может быть соединена только одной работой (т.е. сетевой график не может быть мультиграфом). Для устранения этой ситуации вводится дополнительное событие и фиктивная работа.
5) Пара событий может быть соединена только одной работой (т.е. сетевой график не может быть мультиграфом). Для устранения этой ситуации вводится дополнительное событие и фиктивная работа.










 : или
: или











 2 – событие 1-го ранга;
2 – событие 1-го ранга;


