
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні настанови щодо виконання завдання 5Содержание книги
Поиск на нашем сайте
Побудувати переріз заданої кривої поверхні площиною загального положення. Розв’язання задачі розглянуто на прикладі (див. рис. 14), коли крива поверхня задана похилим конусом, а січна площина прямими m і n, які перетинаються, з використанням допоміжного косокутного проекціювання. 1. Для визначення перетину твірних поверхні з січною площиною, переводимо її з загального положення в проекціююче положення, (див. п.1, 4 пояснення до завдання 4). При косокутному проекціюванні в напрямку однієї з ліній січної площини, вона спроекціюється в пряму лінію на відповідній площині проекцій. Напрямом допоміжного косокутного проекціювання вибираємо пряму m. Тому з M2 та N2 (які вибрані довільно) проведемо допоміжні проекціюючі промені паралельно m2 до перетину з віссю x1 2 . Перетин ліній проекціювального зв’язку з допоміжними проекціювальними променями на площині П1, проведеними з M1 та N1 паралельно напрямку проекціювання, визначить допоміжні проекції та 2. Конус проекціюємо на площину П1 в тому ж напрямку що і площину mn. Основа конуса належить площині П1, тому вона буде незмінна. З вершини S2 проведемо допоміжний проекціювальний промінь до перетину з віссю x1 2 . З 3. Позначаємо контурні твірні конуса на площинах проекцій: на площині П2 це твірні S2A2 та S2B2, а на площині П1 – S1C1 та S1D1. Будуємо допоміжні твірні SE та SK, у яких точки Е і К на площині П2 збігають.
25.
Рис. 14. Приклад виконання завдання 5 26. 4. З’єднаємо точки основи А1, В1, С1, D1, Е1, К1 з допоміжною проекцією вершини конуса
5. Проекціювання кожної точки перерізу в зворотному напрямку, паралельно попередньому, на відповідну проекцію твірної, визначить горизонтальну 112131415161 і фронтальну 122232425262 проекції перерізу. 6. Визначимо видимість перерізу (еліпса) на площинах проекцій. Переріз на ділянці 4151216131 на площину П1 проекціюється як видимий, тому що твірні,
на яких розташовані точки, проекціються як видимі. Переріз на ділянці 12326222 на площину П2 проекціюється як невидимий, тому що твірні, на яких розташовані точки, проекціються як невидимі. Завдання 6. Перетин геометричних тіл прямою лінією та побудова розгортки Умова: Побудувати перетин заданих поверхонь призми, піраміди, циліндра, конуса, сфери відрізком прямої. Визначити видимість прямої на проекціях. Побудувати розгортку поверхні з нанесенням точок перетину прямої з поверхнею. Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 6 збірника завдань. Методичні настанови щодо виконання завдання 6 Визначити точки перетину поверхонь призми, піраміди, циліндра, конуса, кулі відрізком прямої. Визначити видимість на проекціях. Побудувати розгортку поверхні з нанесенням точок перетину прямої з поверхнею. В прикладі (див. рис. 15), для визначення точок перетину прямої з поверхнею похилого конуса, використовується допоміжне центральне косокутне проекціювання. Центр проекціювання – вершина конуса. 1. На заданій прямій виберемо довільні точки А і В. Проведемо проекціювальні промені з вершини S2 через А2 та В2. З допоміжних проекцій
проведеними з вершини S1 через А1 та В1.
27.
Рис. 15. Приклад виконання завдання 6 28. 2. Перетин допоміжної проекції прямої 3. Визначити видимість прямої на площинах проекцій дозволить місце розташування точок М1 і N1. Горизонтальна проекція прямої до точки М1 проекціюється як видима, тому що точка М1 розташована на видимій частині поверхні конуса. Між точками перетину і після точки N1 пряма проекціюється як невидима. Так саме визначиться видимість фронтальної проекції прямої. 4. Суміщення поверхні з площиною називають розгорткою. Для поверхні конуса використаємо метод апроксимації – наближення.
Вписавши в конус правильну піраміду з восьмикутником 1121314151617181 в основі і вершиною конуса S1, наблизимо криву поверхню до граної. 5. Використовуючи обертання кожного ребра вписаної піраміди навколо вісі, яка проходить через вершину S 1 і перпендикулярна до площини проекцій Π1, визначимо НВ бічних ребер піраміди. 6. В довільному місці проведемо пряму, на якій відкладемо НВ бічного ребра піраміди S 2 1¯2. З точки 10 проведемо дугу радіусом 1121, а з точки S0 дугу радіусом S 2 2¯2. Будуємо інші точки основи піраміди (конуса). Побудовані точки з’єднаємо за допомогою лекала. Дотично до лекальної кривої будуємо коло основи. 7. Побудова на розгортці точок перетину прямої з поверхнею похилого конуса зрозуміла з приклада. Завдання 7. Взаємний перетин багатогранників Умова: Побудувати лінію взаємного перетину заданих багатогранників. Показати видимість на площинах проекцій. Завдання виконати на форматі А4. Варіанти наведені в табл. 7 збірника завдань.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.128.229 (0.007 с.) |

 1
1 ≡
≡  1, через які пройде слід площини
1, через які пройде слід площини  на площині проекцій П1.
на площині проекцій П1. направимо лінію проекціювального зв’язку до перетину з допоміжним проекціювальним променем, який пройшов з вершини S1 паралельно напрямку проекціювання. Допоміжну проекцію вершини конуса
направимо лінію проекціювального зв’язку до перетину з допоміжним проекціювальним променем, який пройшов з вершини S1 паралельно напрямку проекціювання. Допоміжну проекцію вершини конуса  з’єднаємо з колом основи.
з’єднаємо з колом основи.
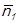 визначать допоміжні проекції точок перерізу:
визначать допоміжні проекції точок перерізу: =
=  ∩
∩ 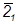 =
=  ∩
∩  =
=  ∩
∩  =
=  ∩
∩  =
= 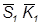 ∩
∩  =
=  ∩
∩ 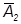 та
та  проведемо лінії зв’язку до перетину з проекціювальними променями
проведемо лінії зв’язку до перетину з проекціювальними променями
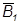 з колом основи, в яке спроекціювалася бічна поверхня конуса, визначить допоміжні проекції точок перетину. Проекції M1 та N1 побудовані за допомогою зворотних променів. Проекції M2 та N2 будуємо використовуючи належність точки до прямої.
з колом основи, в яке спроекціювалася бічна поверхня конуса, визначить допоміжні проекції точок перетину. Проекції M1 та N1 побудовані за допомогою зворотних променів. Проекції M2 та N2 будуємо використовуючи належність точки до прямої.


