
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні настанови щодо виконання завдання 1Содержание книги
Поиск на нашем сайте НАРИСНА ГЕОМЕТРІЯ
Методичні вказівки до самостійного виконання розрахунково-графічних робіт студентів усіх напрямів підготовки факультету МКТ
Київ КНУТД 2014 Нарисна геометрія: Методичні вказівки до самостійного виконання розрахунково-графічних робіт студентів усіх напрямів підготовки факультету МКТ / упор. Ю.А. Ковальов, С.А. Плешко. – К.: КНУТД, 2014. – 34 с.
Упорядники: Ю.А. Ковальов, канд. тех. наук, доцент С.А. Плешко, канд. тех. наук, доцент Робота виконана під загальною редакцією канд. тех. наук, професора М.В. Куща. Відповідальний за випуск: завідувач кафедри інженерної механіки д-р тех. наук, професор В.П. Місяць Затверджено на засіданні кафедри інженерної механіки. Протокол № 10 від 07.03.2014 р. Методичні вказівки розроблені для самостійної роботи студентів при виконанні розрахунково-графічних робіт складених на базі типової програми з нарисної геометрії у відповідності з курсом, що читається в Київському національному університеті технологій та дизайну. У виданні, за конкретними темами, наведені приклади розв’язання задач, настанови по оформленню розрахунково-графічних робіт. Видання розраховане для студентів усіх напрямів підготовки факультету МКТ. Загальні положення Нарисна геометрія вивчається студентами вищих навчальних закладів в перших семестрах навчання і досліджує просторові форми за їх зображеннями на площині. Зображеннями просторових форм користуються представники різних спеціальностей. Нарисна геометрія має свої певні теоретичні обґрунтування. Тільки систематичне і глибоке вивчення цього курсу сприяє розвитку просторового мислення, вмінню уявити просторові форми предметів за їх зображеннями, виконувати креслення об’єктів, що проектуються. Закріплюють знання з теми шляхом самостійного виконання розрахунково-графічних робіт (РГР), які являють собою епюри (кресленики). Їх виконують по мірі послідовного проходження курсу. Завдання для РГР індивідуальні та розроблені по варіантах. Номер його надає викладач. Умови завдань наведені в методичних матеріалах „Нарисна геометрія: Збірник завдань до самостійної роботи студентів усіх напрямів підготовки факультету МКТ при виконанні розрахунково-графічних робіт / упор.: Ю.А. Ковальов, С.А. Плешко – К.: КНУТД, 2014. – 15 с.” Приклади розв’язання задач та методичні настанови наведені вцих м етодичних вказівках. При оформленні завдань слід додержуватись таких вимог: 1. Завдання виконують на аркушах папері для креслення стандартного формату А4 (297х210) або А3 (297х420). На подальшому всі розміри визначаються в міліметрах (мм). 2. Кресленик (умова та рішення) має рівномірно заповнювати формат. 3. Написи виконують стандартним шрифтом розміром 5 або 7 згідно з ГОСТ 2.304-81. 4. Побудови виконують використовуючи інструменти для креслення та олівці: з грифелем ТМ або НВ для проведення тонких ліній та наведення кресленика, а з м’яким грифелем М або В – для виконання написів. 5. Товщина ліній на кресленику повинна становити (ГОСТ 2.303-68): лінія суцільна товста основна (лінії видимого контуру) – 0,8...1,4; лінія штрихова (лінії невидимого контуру) – 0,4...0,7; лінії виносні, розмірні, осьові, горизонтального та вертикального зв’язку та лінії допоміжної побудови – 0,3...0,4. 6. Проекції точок позначають кружками діаметром 1...2 мм. 7. Послідовність дій у графічній роботі має бути зазначена стрілками на відповідних лініях. Стрілками позначають напрям проекціювання. Також повинна бути відображена видимість геометричних елементів. 8. На аркуші РГР мають бути: • внутрішня рамка, яку виконують суцільною товстою основною лінією, відступивши з лівого боку 20 мм, з правого боку, знизу, зверху по 5 мм; 3. • у лівому верхньому куті записують номер завдання та його тему без скорочень (рис. 1);
Рис. 1 • у правому верхньому куті виконують таблицю з координатами точок (рис. 2) або наклеюють варіант умови задачі; • у правому нижньому куті зазначається номер варіанту, академічна група, прізвище студента (рис. 3).
Рис. 2 Рис. 3
4.
Рис. 4 Альбом графічних робіт оформляється титульним аркушем. На прикладі оформлення титульного листа (рис. 4) в дужках зазначені номери шрифтів для кожного напису. Показані на прикладі осьові лінії (штрихпунктирні) є висями симетрії для компоновки написів. Після завершення роботи вони видаляються. Титульний лист і графічні роботи за номерами підшивають в альбом, який студент особисто, у визначений термін, здає викладачу. Викладач підписує альбом після захисту всіх робіт студентом. Без підписаного викладачем альбому графічних робіт студент до екзамену або заліку не допускається.
5. Завдання 1. Визначення положення та величин ребер багатогранника за їх проекціями Умова. В заданому багатограннику: а) визначити положення ребер відносно площин проекцій; б) позначити подвійною лінією проекції ребер, які проекціюються в натуральну величину, та подвійною дугою проекції кутів нахилу ребер до площин проекцій П1 та П2; в) визначити натуральну величину одного з ребер загального положення, кути нахилу його до площин проекцій та побудувати проекції слідів цього ребра на площинах проекцій; д) одне з ребер загального положення поділити точкою у відношенні 2:3. Завдання виконати на аркуші формату А4. Варіанти завдань наведені в табл. 1 збірника завдань. Рис. 5. Приклад виконання завдання 1 8. Завдання 2. Площина. Взаємно перпендикулярні та паралельні площини Умова: а) Визначити натуральну величину відстані від точки D до площини заданої трикутним відсіком АВС; б) побудувати площинку яка паралельна площині DEK та віддалена від неї на 35 мм; в)через пряму DK провести площину яка перпендикулярна до заданої площини АВС. Побудувати лінію їх взаємного перетину та визначити видимість елементів площин в проекціях. Позначити проекції кута між прямою DK та площиною АВС. Завдання виконати на 3 аркушах формату А4 в масштабі 1:1. Координати точок по варіантах наведені в табл. 2 збірника завдань. Рис. 12. Приклад виконання завдання 3 д 22.
Рис. 13. Приклад виконання завдання 4 23. 1. Розташування січної площини в проекціювальному положенні дозволяє легко знайти точки перерізу – точки перетину проекцій ребер багатогранника зі слідом січної площини. Для перетворення січної площини в проекціювальне положення замінимо площину проекцій П2 на нову площину П4 ,яку розташуємо перпендикулярно до сліду січної площини. Проведемо нову вісь x1 4 перпендикулярно до горизонтального сліду h1 площині. Площина П1 стала незмінною. 2. Будуємо проекцію сліду січної площини на площині П4. Якщо січна площина перпендикулярна до П4, проекції точок січної площини будуть розташовані на прямій перетину заданої площини з новою площиною проекцій П4, тобто на сліді. В прикладі такою точкою є довільна точка Ν2 на сліді f2. Будуємо проекцію вибраної точки на П4. Відстань від Ν4 до нової вісі x1 4 дорівняє відстані від Ν 2 до x1 2 . Через Ν4 і точку перетину горизонтального сліду h1 з x14 проходить слід f4. 3. Будуємо проекцію піраміди на площині П4. Фронтальна проекція основи піраміди збігає з віссю x1 2 , тому на новій площині проекцій П4 вона також буде збігати з віссю x1 4 . Перетин ліній зв’язку, проведених з незмінних проекцій А1, В1, С1, D1, з новою віссю x1 4 , визначить проекції вершин основи А4, В4, С4, D4 на площині П4. Вершину піраміди S4 на площині П4 (відстань від S4 до нової вісі x1 4 дорівняє відстані від S2 до x1 2 ) з’єднаємо з проекціями вершин основи А4, В4, С4, D4 . 4. Перетин сліду заданої січної площини f4 з проекціями ребер визначить точки перерізу 1234 (1 = f ∩ SА; 2 = f ∩ SВ; 3 = f ∩ SС; 4 = f ∩ SD). Кожну точку перерізу проекціюємо в зворотному напрямку на проекції ребер, яким ці точки належать. 5. З’єднаємо точки перерізу, визначаючи видимість його на площинах проекцій. Якщо грань проекціюється на площину проекцій як видима, то і лінія перерізу на цій грані спроекціюється на площину проекцій як видима. 6. Для визначення НВ перерізу замінимо площину проекцій П4 на нову площину П5, яка паралельна до перерізу. Проведемо нову вісь x45 паралельно до перерізу 14243444. Визначимо проекції 15, 25, 35, 45,відкладаючи відстань від замінних проекцій 11, 21, 31, 41 до замінної вісі x1 4 (наприклад, від 11 до x1 4 ). Чотирикутник 15253545 визначить НВ перерізу.
24. Завдання 5. Перетин поверхні циліндра, конуса, сфери площиною Умова: Побудувати переріз заданої кривої поверхні площиною загального положення. Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 5 збірника завдань. Рис. 14. Приклад виконання завдання 5 26. 4. З’єднаємо точки основи А1, В1, С1, D1, Е1, К1 з допоміжною проекцією вершини конуса
5. Проекціювання кожної точки перерізу в зворотному напрямку, паралельно попередньому, на відповідну проекцію твірної, визначить горизонтальну 112131415161 і фронтальну 122232425262 проекції перерізу. 6. Визначимо видимість перерізу (еліпса) на площинах проекцій. Переріз на ділянці 4151216131 на площину П1 проекціюється як видимий, тому що твірні, на яких розташовані точки, проекціються як видимі. Переріз на ділянці 12326222 на площину П2 проекціюється як невидимий, тому що твірні, на яких розташовані точки, проекціються як невидимі. Завдання 6. Перетин геометричних тіл прямою лінією та побудова розгортки Умова: Побудувати перетин заданих поверхонь призми, піраміди, циліндра, конуса, сфери відрізком прямої. Визначити видимість прямої на проекціях. Побудувати розгортку поверхні з нанесенням точок перетину прямої з поверхнею. Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 6 збірника завдань. Рис. 15. Приклад виконання завдання 6 28. 2. Перетин допоміжної проекції прямої 3. Визначити видимість прямої на площинах проекцій дозволить місце розташування точок М1 і N1. Горизонтальна проекція прямої до точки М1 проекціюється як видима, тому що точка М1 розташована на видимій частині поверхні конуса. Між точками перетину і після точки N1 пряма проекціюється як невидима. Так саме визначиться видимість фронтальної проекції прямої. 4. Суміщення поверхні з площиною називають розгорткою. Для поверхні конуса використаємо метод апроксимації – наближення. Вписавши в конус правильну піраміду з восьмикутником 1121314151617181 в основі і вершиною конуса S1, наблизимо криву поверхню до граної. 5. Використовуючи обертання кожного ребра вписаної піраміди навколо вісі, яка проходить через вершину S 1 і перпендикулярна до площини проекцій Π1, визначимо НВ бічних ребер піраміди. 6. В довільному місці проведемо пряму, на якій відкладемо НВ бічного ребра піраміди S 2 1¯2. З точки 10 проведемо дугу радіусом 1121, а з точки S0 дугу радіусом S 2 2¯2. Будуємо інші точки основи піраміди (конуса). Побудовані точки з’єднаємо за допомогою лекала. Дотично до лекальної кривої будуємо коло основи. 7. Побудова на розгортці точок перетину прямої з поверхнею похилого конуса зрозуміла з приклада. Завдання 7. Взаємний перетин багатогранників Умова: Побудувати лінію взаємного перетину заданих багатогранників. Показати видимість на площинах проекцій. Завдання виконати на форматі А4. Варіанти наведені в табл. 7 збірника завдань. Рис. 17. Приклад виконання завдання 8 32. 1. Визначимо граничні 1 і 5 точки взаємного перетину. Контурні твірні похилого циліндра на П1 перетинають в точках 11 і 51 з колом основи прямого циліндра, в яке проекціюється його бічна поверхня. Перетин ліній зв’язку з фронтальними проекціями контурних твірних похилого циліндра на П1 визначить шукані точки 12 і 52. 2. Граничні точки А і В будуємо з використання допоміжної січної площини Σ (Σ1 ┴ Π1). 3. Побудову проміжних точок розглянемо на прикладі точок 4 і 6. Допоміжна фронтальна січна площина перетне бокову поверхню циліндрів по твірним, в тому числі похилий циліндр по твірним 41 і 61. Перетин фронтальних проекцій 4¯2 і 6¯2 з відповідними твірними прямого циліндра визначить шукані точки 42 і 62. 4. З’єднаємо побудовані точки з урахування видимість лінії перетину. Точки 51, 41 ≡ 61, 31 ≡ 71 розташовані на видимій частині поверхонь циліндрів. Фронтальна проекція лінії перетину на ділянці 7262524232 спроекціюється як видима. Завдання 9. Утворення і зображення кривих поверхонь Умова. Побудувати проекції кривих поверхонь Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 9 збірника завдань. НАРИСНА ГЕОМЕТРІЯ
Методичні вказівки до самостійного виконання розрахунково-графічних робіт студентів усіх напрямів підготовки факультету МКТ
Київ КНУТД 2014 Нарисна геометрія: Методичні вказівки до самостійного виконання розрахунково-графічних робіт студентів усіх напрямів підготовки факультету МКТ / упор. Ю.А. Ковальов, С.А. Плешко. – К.: КНУТД, 2014. – 34 с.
Упорядники: Ю.А. Ковальов, канд. тех. наук, доцент С.А. Плешко, канд. тех. наук, доцент Робота виконана під загальною редакцією канд. тех. наук, професора М.В. Куща. Відповідальний за випуск: завідувач кафедри інженерної механіки д-р тех. наук, професор В.П. Місяць Затверджено на засіданні кафедри інженерної механіки. Протокол № 10 від 07.03.2014 р. Методичні вказівки розроблені для самостійної роботи студентів при виконанні розрахунково-графічних робіт складених на базі типової програми з нарисної геометрії у відповідності з курсом, що читається в Київському національному університеті технологій та дизайну. У виданні, за конкретними темами, наведені приклади розв’язання задач, настанови по оформленню розрахунково-графічних робіт. Видання розраховане для студентів усіх напрямів підготовки факультету МКТ. Загальні положення Нарисна геометрія вивчається студентами вищих навчальних закладів в перших семестрах навчання і досліджує просторові форми за їх зображеннями на площині. Зображеннями просторових форм користуються представники різних спеціальностей. Нарисна геометрія має свої певні теоретичні обґрунтування. Тільки систематичне і глибоке вивчення цього курсу сприяє розвитку просторового мислення, вмінню уявити просторові форми предметів за їх зображеннями, виконувати креслення об’єктів, що проектуються. Закріплюють знання з теми шляхом самостійного виконання розрахунково-графічних робіт (РГР), які являють собою епюри (кресленики). Їх виконують по мірі послідовного проходження курсу. Завдання для РГР індивідуальні та розроблені по варіантах. Номер його надає викладач. Умови завдань наведені в методичних матеріалах „Нарисна геометрія: Збірник завдань до самостійної роботи студентів усіх напрямів підготовки факультету МКТ при виконанні розрахунково-графічних робіт / упор.: Ю.А. Ковальов, С.А. Плешко – К.: КНУТД, 2014. – 15 с.” Приклади розв’язання задач та методичні настанови наведені вцих м етодичних вказівках. При оформленні завдань слід додержуватись таких вимог: 1. Завдання виконують на аркушах папері для креслення стандартного формату А4 (297х210) або А3 (297х420). На подальшому всі розміри визначаються в міліметрах (мм). 2. Кресленик (умова та рішення) має рівномірно заповнювати формат. 3. Написи виконують стандартним шрифтом розміром 5 або 7 згідно з ГОСТ 2.304-81. 4. Побудови виконують використовуючи інструменти для креслення та олівці: з грифелем ТМ або НВ для проведення тонких ліній та наведення кресленика, а з м’яким грифелем М або В – для виконання написів. 5. Товщина ліній на кресленику повинна становити (ГОСТ 2.303-68): лінія суцільна товста основна (лінії видимого контуру) – 0,8...1,4; лінія штрихова (лінії невидимого контуру) – 0,4...0,7; лінії виносні, розмірні, осьові, горизонтального та вертикального зв’язку та лінії допоміжної побудови – 0,3...0,4. 6. Проекції точок позначають кружками діаметром 1...2 мм. 7. Послідовність дій у графічній роботі має бути зазначена стрілками на відповідних лініях. Стрілками позначають напрям проекціювання. Також повинна бути відображена видимість геометричних елементів. 8. На аркуші РГР мають бути: • внутрішня рамка, яку виконують суцільною товстою основною лінією, відступивши з лівого боку 20 мм, з правого боку, знизу, зверху по 5 мм; 3. • у лівому верхньому куті записують номер завдання та його тему без скорочень (рис. 1);
Рис. 1 • у правому верхньому куті виконують таблицю з координатами точок (рис. 2) або наклеюють варіант умови задачі; • у правому нижньому куті зазначається номер варіанту, академічна група, прізвище студента (рис. 3).
Рис. 2 Рис. 3
4.
Рис. 4 Альбом графічних робіт оформляється титульним аркушем. На прикладі оформлення титульного листа (рис. 4) в дужках зазначені номери шрифтів для кожного напису. Показані на прикладі осьові лінії (штрихпунктирні) є висями симетрії для компоновки написів. Після завершення роботи вони видаляються. Титульний лист і графічні роботи за номерами підшивають в альбом, який студент особисто, у визначений термін, здає викладачу. Викладач підписує альбом після захисту всіх робіт студентом. Без підписаного викладачем альбому графічних робіт студент до екзамену або заліку не допускається.
5. Завдання 1. Визначення положення та величин ребер багатогранника за їх проекціями Умова. В заданому багатограннику: а) визначити положення ребер відносно площин проекцій; б) позначити подвійною лінією проекції ребер, які проекціюються в натуральну величину, та подвійною дугою проекції кутів нахилу ребер до площин проекцій П1 та П2; в) визначити натуральну величину одного з ребер загального положення, кути нахилу його до площин проекцій та побудувати проекції слідів цього ребра на площинах проекцій; д) одне з ребер загального положення поділити точкою у відношенні 2:3. Завдання виконати на аркуші формату А4. Варіанти завдань наведені в табл. 1 збірника завдань. Методичні настанови щодо виконання завдання 1 За координатами вершин будуємо проекції багатогранника (приклад виконання на рис. 5). В заданому багатограннику: а) визначити положення ребер багатогранника відносно площин проекцій. Аналізуємо розташування проекції ребер відносно вісі x12. Якщо вони паралельні або перпендикулярні до вісі (одна проекція або дві) – ребро займає особливе (часткове) положення, а якщо під кутом до вісі – загальне положення. б) подвійною лінією позначити проекції ребер, які проекціюються в натуральну величину та подвійною дугою проекції кутів нахилу ребер до площин проекцій П 1 і П 2. Ребро, яке займає особливе положення, проекціюється на відповідну площину (або площини) проекцій в натуральну величину (НВ) тапозначається подвійною тонкою лінією або поруч з проекцією проводять тонку лінію. На цю ж площину проекцій в НВ проекціюється і кут нахилу ребра до іншої площини проекцій. Це кут між проекцією ребра в НВ та горизонтальною лінією, яка паралельна вісі x1 2 . Він позначається подвійною дугою. в) визначити НВ одного з ребер загального положення, кути нахилу його до площин проекцій П1 і П2. Для визначення НВ ребра використаємо спосіб прямокутного трикутника. 1. Будуємо перпендикуляр до проекції ребра загального положення C1S1 в одній із точок, наприклад S1. Всі побудови пропонуємо виконувати в напрямку протилежному від проекцій багатогранника. 2. На перпендикулярі відкладемо різницю відстаней (координат) кінців іншої проекції ребра до вісі x1 2 . Так на горизонтальній проекції відкладемо різницю аплікат (по вісі z) - zs-zс, а на фронтальній – різницю ординат (по вісі y) – yс - ys. 3. Побудовану точку позначимо літерою S1', яка відповідає літері S1 кінця ребра. Відрізок C1S1' – НВ ребра CS.
6. 4. Кут між НВ ребра C1S1' та його проекцією C1S1 є НВ кута α нахилу ребра до горизонтальної площини проекцій П 1. Для визначення НВ кута β нахилу ребра до фронтальної площини проекцій П2 виконаємо аналогічну побудову з використанням фронтальної проекції ребра C2S2. г) побудувати проекції слідів цього ребра на площинах проекцій П1 та П2. Слід – це точка перетину прямої з площиною проекцій. 1. Для побудови проекцій горизонтального сліду H ребра CS подовжимо фронтальну проекцію ребра C2S2 до перетину з x12 – отримаємо фронтальну проекцію H2 горизонтального сліду. З H2 проведемо лінію зв’язку (ці лінії завжди перпендикулярні до вісі проекцій) до перетину з подовженням проекції C1S1. Горизонтальну проекцію горизонтального сліду позначимо літерою H1. 2. Подовження горизонтальної проекції ребра C1S1 до перетину з віссю x12 дає горизонтальну проекцію фронтального сліду – F1. Точка перетину лінії зв’язку з подовженням фронтальної проекції ребра C2S2 – фронтальна проекція фронтального сліду F2. д) одне з ребер загального положення поділити точкою у відношенні 2:3. Поділимо ребро (наприклад, CS)у заданому відношенні, використовуючи властивості подібності трикутників. З одного кінця ребра (наприклад, C2), під довільним кутом, проведемо допоміжну пряму, на якій відкладемо п’ять (2+3) рівних відрізків довільної довжини. Сполучимо точки S2 та 5. Паралельно відрізку S25, через точку 2 проведемо пряму до перетину з C2S2. Отримаємо точку N2 (C2N2: N2S2 = 2:3). Використовуючи належність точки до прямої визначимо Ν1. Точка Ν поділяє ребро CS у заданому відношенні.
7.
Рис. 5. Приклад виконання завдання 1 8. Завдання 2. Площина. Взаємно перпендикулярні та паралельні площини Умова: а) Визначити натуральну величину відстані від точки D до площини заданої трикутним відсіком АВС; б) побудувати площинку яка паралельна площині DEK та віддалена від неї на 35 мм; в)через пряму DK провести площину яка перпендикулярна до заданої площини АВС. Побудувати лінію їх взаємного перетину та визначити видимість елементів площин в проекціях. Позначити проекції кута між прямою DK та площиною АВС. Завдання виконати на 3 аркушах формату А4 в масштабі 1:1. Координати точок по варіантах наведені в табл. 2 збірника завдань.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |






 . Точки перетину допоміжних проекцій твірних зі слідом площини
. Точки перетину допоміжних проекцій твірних зі слідом площини  ≡
≡ 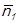 визначать допоміжні проекції точок перерізу:
визначать допоміжні проекції точок перерізу: =
=  ∩
∩ 
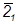 =
=  ∩
∩  =
=  ∩
∩  =
=  ∩
∩  =
= 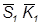 ∩
∩  =
=  ∩
∩ 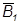 з колом основи, в яке спроекціювалася бічна поверхня конуса, визначить допоміжні проекції точок перетину. Проекції M1 та N1 побудовані за допомогою зворотних променів. Проекції M2 та N2 будуємо використовуючи належність точки до прямої.
з колом основи, в яке спроекціювалася бічна поверхня конуса, визначить допоміжні проекції точок перетину. Проекції M1 та N1 побудовані за допомогою зворотних променів. Проекції M2 та N2 будуємо використовуючи належність точки до прямої.



