
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні настанови щодо виконання завдання 3Содержание книги
Поиск на нашем сайте В заданому багатограннику визначити: а) відстань між зазначеними паралельними ребрами. Відстань зображується в НВ, якщо ребра займають проекціююче положення відносно до однієї з площин проекцій. Для приведення прямих в таке положення, використовується один із способів перетворення комплексного кресленика: заміна площин проекцій, плоско-паралельне переміщення, обертання тощо.
14. 1. Розв’язання задачі з використанням заміни площин проекцій. 1.1. Замінимо одну з площин проекцій на нову. Для цього проводимо вісь проекцій параллельно до горизонтальних або фронтальних проекцій заданих ребер. Площина, на якій розташовані ці проекції, стане незмінною. 1.2. З незмінних проекцій точок багатогранника проведемо лінії зв’язку на нову площину проекцій. На відповідних лініях зв’язку, від нової вісі проекцій відкладемо координати точок на замінній площині проекцій, а саме відстань від замінної проекції точки до замінної вісі проекцій. 1.3. З’єднаємо відповідні проекції точок на новій площині. Новоутворені проекції ребер, що спроекціювалися в НВ, позначимо подвійною лінією. 1.4. Виконаємо другу заміну, а саме: замінимо площину проекцій, з якої виконувалась остання побудова, на нову, яка розташована перпендикулярно до заданих ребер. На комплексному кресленику проведемо нову вісь проекцій перпендикулярно НВ ребер. 1.5. З незмінної площини проекцій проведемо лінії зв’язку на нову площину проекцій. На відповідній лінії зв’язку, від нової вісі проекцій відкладемо координати точок з замінної площині. 1.6. З’єднаємо побудовані проекції точок. Відстань між точками, в які спроекціювалися задані ребра, визначить відстань між ними. 2. Розв’язання задачі з використанням плоско-паралельного переміщення. 2.1. Перемістимо багатогранник, без зміни його розмірів, паралельно до одній з площин проекцій. Переміщення закінчимо, коли проекції заданих ребер будуть паралельні до вісі x1 2 . 2.2. При переміщенні фігури паралельно до однієї з площини проекцій, точки фігури переміщуються в площинах паралельних до цієї площини. Тому на іншій площині проекцій, проекції точок фігури переміщуються по слідам площин, які паралельні до вісі x1 2 . Використовуючи це правило, а також лінії зв’язку, визначимо іншу проекцію багатогранника. 2.3. Перемістимо нову проекцію багатогранника без зміни його розмірів. Переміщення закінчимо, коли проекції заданих ребер розташуються перпендикулярно до вісі x1 2 У відповідності з пунктом 2.2, визначимо іншу проекцію багатогранника. Відстань між точками, в які спроекціювалися задані ребра, визначить відстань між ними. б) найкоротшу відстань між зазначеними мимобіжними ребрами (приклад виконання на рис. 9). Перпендикуляр з точки, в яку після перетворення спроекціюється одне з ребер, на проекцію іншого ребра, визначить потрібну відстань. Задачу розв’яжемо з використанням заміни площин проекцій. 1. Замінимо площину П2 на нову площину П4, яку розташуємо паралельно до одного з заданих ребер. На кресленику нову вісь проекцій x1 4 проведемо паралельно до ребра С1S1. Площина П1 стане незмінною. 2. З незмінних проекцій А1, В1, С1, S1 проведемо лінії зв’язку на нову площину проекцій. 3. На лініях зв’язку, від нової вісі проекцій x14, на нову площину П4, відкладемо координати точок на замінній площині П2. Наприклад, від В2 до x1 2 , від S2 до x1 2 . 4. З’єднаємо проекції точок на площині П4 між собою, а проекцію ребра С4S4, що спроекціювалося в НВ, позначимо подвійною лінією. 5. Замінимо площину П4 на нову площину П5, яка розташована перпендикулярно до заданого ребра. Площина проекцій П4 стане незмінною. Проведемо нову вісь x45 перпендикулярно до ребра С4S4. 6. З незмінної площини П4 проведемо лінії зв’язку на нову площину проекцій П5. Від нової вісі x45 на нову площину П5, відкладемо координати точок на замінній площині П1. На приклад, від В1 до x1 4 , від S1 до x1 4 . 7. Перпендикуляр з точки С5 ≡ S5, в яку спроекціювалося задане ребро СS, на проекцію А5В5 іншого заданого ребра, визначить НВ відстані між ребрами. в) відстань від вершини до ребра або грані. Для визначення відстані від вершини до ребра, треба одним зі способів перетворення комплексного кресленика перевести задане ребро в проекціювальне положення – точку. Відстань від цієї точки до проекції вершини визначить шукану відстань. Відстань від вершини до грані буде визначена, якщо грань переведена в проекціювальне положення – в пряму лінію. Перпендикуляр з проекції заданої вершини на проекцію грані (пряму) визначить НВ відстані. Розглянемо розв’язання задачі на прикладі ( див. рис. 10 ) з використанням заміни площин проекцій. 1. Щоб грань АВS зайняла проекціювальне положення треба нову площину П4 розташувати перпендикулярно до неї. Проведемо горизонталь h грані АВS. 2. Замінимо площину П2 на нову площину П4, яка перпендикулярна до горизонталі h. Проведемо нову вісь x1 4 перпендикулярно до горизонталі h1 Площина П1 стане незмінною. 3. З незамінних проекцій А1, В1, С1 , S1 проведемо лінії зв’язку. 4. Від нової вісі x1 4 , на площину проекцій П4, відкладемо координати точок з замінної площині проекцій П2. Наприклад, від В2 до x1 2 , від S2 до x1 2 , від А2 до x1 2 .
16.
17. 5. Задана грань АВS на площину П4 спроекціювалась в пряму лінію. Перпендикуляр з вершини С4 на проекцію грані А4В4S4 визначить шукану величину. г) відстань від ребра до паралельної йому грані. Задану грань треба перевести, після відповідного перетворення, в проекціююче положення – в пряму. Відстань визначиться перпендикуляром з проекції заданого ребра на пряму, в яку спроекціюється задана грань. г) відстань між паралельними гранями. Задані грані, після відповідного перетворення, треба перевести в проекціююче положення – в прямі. Відстань визначиться перпендикуляром між прямими, в які спроекціюються грані. д) визначити величину кута між двома гранями при зазначеному ребрі (приклад виконання на рис. 7). Розглянемо розв’язання задачі на прикладі з використанням плоско-паралельного переміщення. 1. На площині П1 перемістимо проекцію багатогранника без зміни її розмірів. Переміщення закінчимо, коли проекція зазначеного ребра А1S1 розташується паралельно до x1 2 . 2. На підставі правила (п. 2.2 на стор. 11), на площині П2 кожна точка переміщається по прямій лінії, яка паралельна до x1 2 . 3. За допомогою ліній зв’язку, визначимо проекції точок після переміщення 4. З’єднаємо нові проекції точок між собою, а проекцію зазначеного ребра 5. На площині П2 переміщаємо проекцію багатогранника без зміни її розмірів. Переміщення закінчимо, коли проекція зазначеного ребра 6. На горизонтальній площині проекцій ребро проекціюється в точку
18.
19.
Рис 11. Приклад виконання завдання 3 е 20. д) визначити НВ грані заданої трикутним відсіком (приклад виконання, рис. 12). Розв’яжемо задачу з використанням обертання навколо лінії рівня. Трикутний відсік спроекціюється на площину проекцій в НВ, якщо його, після обертання навколо лінії рівня, розташувати паралельно площині. 1. Проведемо горизонталь h грані АВС. 2. При обертанні грані АВС навколо h вершина А та точка 1 нерухомі, а вершини В та С обертаються в площинах перпендикулярних h. Визначивши НВ радіуса обертання кожної вершини, визначимо і НВ грані. 3. Перпендикуляр з В1 на h1 визначить горизонтальну проекцію радіуса обертання точки навколо горизонталі, а точка О 1 - проекцію центра обертання. 4. За допомогою способу прямокутного трикутника визначимо НВ радіуса R (В1О1 ) обертання вершини В. Подальша побудова зрозуміла з приклада.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

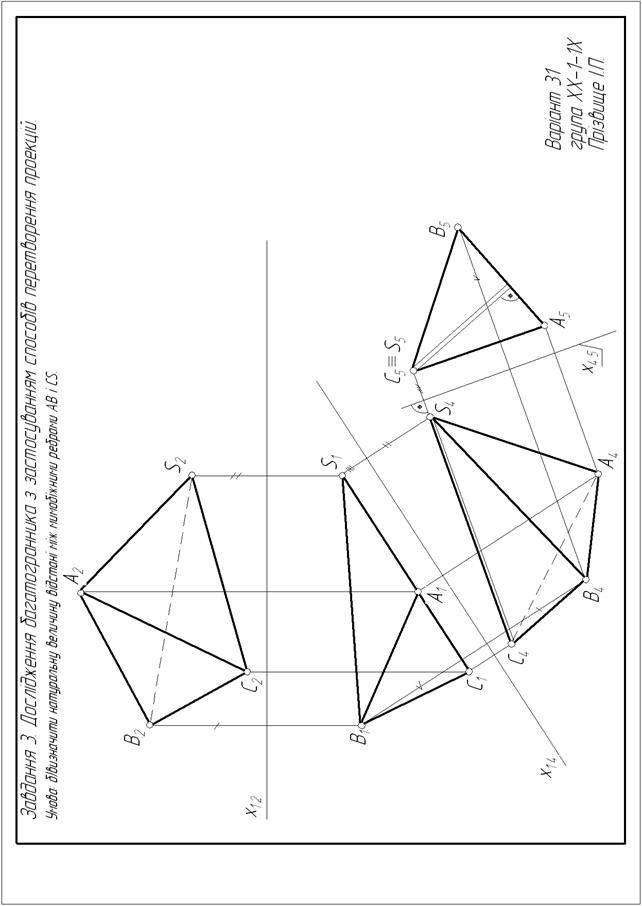 Рис. 9. Приклад виконання завдання 3 б
Рис. 9. Приклад виконання завдання 3 б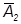 ,
,  ,
, 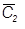 ,
, 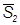 .
.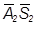 , що спроекціювалася в НВ, позначаємо подвійною лінією.
, що спроекціювалася в НВ, позначаємо подвійною лінією.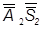 розташується перпендикулярно до x1 2 .
розташується перпендикулярно до x1 2 .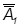 ≡
≡ 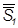 , відповідні грані – в прямі лінії, а кут між ними – в НВ кута при зазначеному ребрі.
, відповідні грані – в прямі лінії, а кут між ними – в НВ кута при зазначеному ребрі.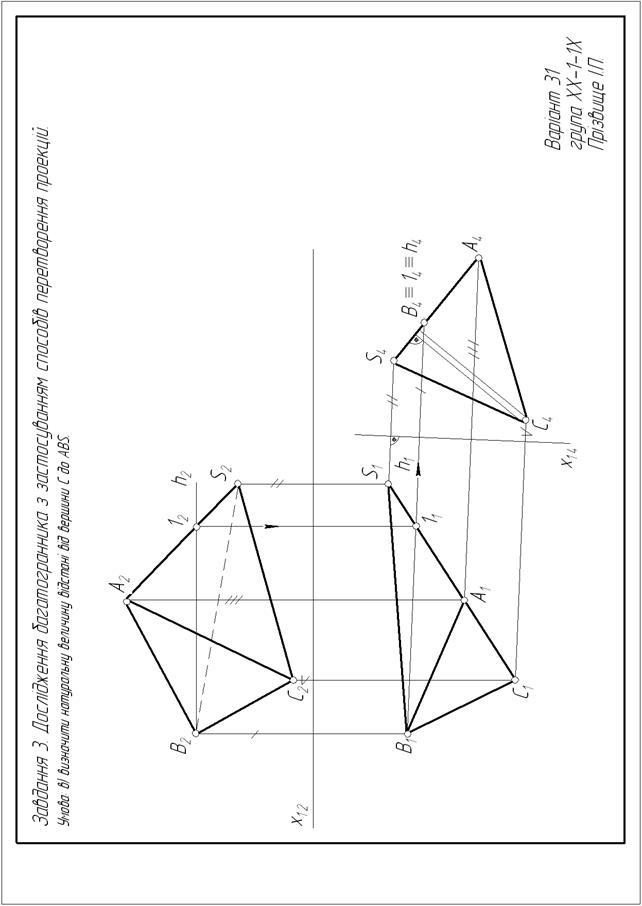 Рис. 10. Приклад виконання завдання 3 в
Рис. 10. Приклад виконання завдання 3 в



