
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие корреляционной зависимостиСодержание книги
Поиск на нашем сайте Виды выборок. 1) собственно случайная выборка. Напр, лото – бочонки с соответствующими номерами помещаются в мешок, они перем-ся, затем бочонки по одному извл-ся из мешка. Выпавшие номера соответствуют единицам, попавшим в выборку; число номеров равно запланиров объему выборки. Отбор жеребьевкой мб подвержен смещениям, вызванным недостатками техники и др причинами. Более надежен с т.зр объективности отбор по таблице случайных чисел. 2) механическая. Часто исп-ся отбор по к-л схеме (так называемая направленная выборка). Схема отбора принимается такой, чтобы отразить осн св-ва и пропорции ген сов-ти. Простейший способ: по спискам единиц ген сов-ти, составленным так, чтобы упорядочивание единиц было бы не связано с изучаемыми свойствами, проводится механический отбор единиц с шагом, равным N. Напр, выбрать опред вокзал, отсчитать 4 путь справа по ходу отправления поездов, сесть в 3 вагон от локомотива и провести опрос пассажира на каждом четном месте. 3) серийная или гнездовая. Напр, серия в промышленности – конфеты, косметические средства, техника. 4) типическая или районированная. Напр, крупный питомник животных или заповедник, где 15% еноты, 25% медведи, 10% рыси, 10% волки, 25% грызуны, 5% лоси, 10% кабаны, то на 100 животных выборка будет представлена 15-ю енотами, 25 медведями, 10 рысями и т.д. 5) динамическая. Выборка во времени. 6) уравновешенная основана на случайном отборе единиц т.обр, что ср размер к-л количеств признака отобранных единиц (для выборки) равен ср размеру этого же признака для всех единиц сов-ти (для ген сов-ти). Уравновешивание по известному количеств признаку представляет собой один из вар-ов типического районирования. Выборку лучше всего производить посредством процесса замещения. Напр, в магазине обуви 20 пар женских сапог на каблуке и 10 пар женских сапог без каблука, а также 20 пар мужской обуви. В уравновешенной выборке будет представлены 2 пары женских сапог на каблуке, 1 пара сапог без каблука и 2 пары мужской обуви. 7) многоступенчатая. Напр, чтобы провести отбор водителей для изучения проблем по орг-ции дорожного движения крупного города, легче провести сначала отбор по классу автомобиля, потом по рыночной стоимости авто, потом выбрать время суток для опроса, затем респ-та. 8) малая выборка (n<30). Напр, группа учащихся. На практике редко прим-ся один вид выборки в чистом виде, как правило, они комбинируются в целях достижения максимальной репрезентативности и экономии. Ошибки выб наблюдения. Разность между показателями выб и ген сов-тей называется ошибкой выборки – μ.Расчет ошибок выборки позволяет оценить репрезентативность (представительность) выб сов-ти.Ошибки выборки характеризуют возможный предел отклонений выборочной средней и выборочной доли от соответственно средней и доли в ген сов-ти.Ошибки выборочного наблюдения: Ошибки регистрации,Ошибки репрезентативности. Ошибки репрезентативности: Случайные (Средние ошибки, Предельные ошибки) и Системные.
24. Собственно-случайная, средняя и предельная ошибки. Коэф доверия. Ср ошибка выборки всегда присутствует в выб иссл-ях и появ-ся вследствие того, что обследуются не все единицы стат сов-ти, а лишь ее часть. Ср ошибка выборки превращается в предельную ошибку Δ при умножении ее на коэф доверия t, к-ый задается предварительно, исходя из требуемой точности наблюдения. Предельная ошибка позволяет судить об «истинном» размере параметра в ген сов-ти с опред степенью вероятности. Ф-лы предельной ошибки случайной выборки при определении средней. Для повторного отбора
Для бесповторного Ф-лы пред ошибки случ выб при определении доли. Для повт 25. Ср и пред ошибка выб в типической выборке. В любом статистическом наблюдении есть ошибки, обусловленные расхождением его результатов с реальной действительностью. Типическая выборка (районированная): средняя ошибка зависит от величины средней дисперсии. Повторный отбор: 26. Понятие о репрезентатисвности выб. Коэф репр. Репрезентативность - представительность выборки экономических показателей (чаще всего статистических), используемых для анализа экономических процессов и явлений. Репрезентативность выборки может быть обеспечена только при объективности отбора данных. Ошибка репрезентативности - расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ - дельта), которая определяется по формуле: Δ=t * m, где t - доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% - 3,0; при вероятности безошибочного прогноза 99,7% - 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента. Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной). 1) Для средних величин
2) Для относительных величин
Сюда же можно и билет 24!! 27. Ошибки выб при разл типах выб, их сравн анализ. В любом статистическом наблюдении есть ошибки, обусловленные расхождением его результатов с реальной действительностью. Точность результатов при малой выборке обычно ниже, чем при выборке большого объема. u=дисперсия/корень(n-1). Билеты 24 и 25 зачитать! 28. Определение необх числ-ти выб. Разрабатывая программу выборочного набл, задаются конкретным значением пред ошибки и уровнем вероятности. Неизвестной остается миним числ-ть выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зав-ти от типа выборки. Для повторной n = Вариация (
29. Практич применение рез-ов выб иссл-ия 30. Способы распр данных выб набл на ген сов-ть. Методы переноса выб данных на ген сов-ть: метод взвешивания; метод перевзвешивания; метод заполнения случайным подбором в классах замещения.
31. Изучение взаимосвязи соц-эк явлений как важнейшая задача стат науки Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отно-шения между явлениями, что позволяет выявлять факторы(признаки), оказывающие ос-новное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения– это такая связь явлений и процессов, когда изменение одного из них– при-чины ведет к изменению другого– следствия. Финансово-экономические процессы представляют собой результат одновременно-го воздействия большого числа причин. Следовательно, при изучении этих процессов не-обходимо выявлять главные, основные причины, абстрагируясь от второстепенных. В основе первого этапа статистического изучения связи лежит качественный ана-лиз, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики. Второй этап– построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее. Третий, последний этап– интерпретация результатов, вновь связан с качественны-ми особенностями изучаемого явления. Статистика разработала множество методов изу-чения связей. Выбор метода изучения связи зависит от познавательной цели и задач ис-следования. Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, на-зываются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называются результативными. В статистике различают функциональную и стохастическую зависимости. Функ-циональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Если причинная зависимость проявляется не в каждом отдельном случае, а в об-щем, среднем, при большом числе наблюдений, то такая зависимость называется стохас-тической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению. 32. Осн задачи корелляционно-регрессивного анализа и практика их реализации. • Выявление наличия (или отсутствия) коррел связи между изучаемыми признаками. • Определение формы коррел зав-ти, т.е. вида ф-ии регрессии (линейной, логарифмической, параболической и др). • Построение уравнения регрессии. • Оценка степени тесноты коррел связи. Аналитические группировки. Явления общественной жизни и отражающие их признаки тесно взаимосвязаны. Аналитическая - группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками. Аналитические группировки позволяют изучить многообразие связей и зависимости между варьирующими признаками. Всю совокупность признаков можно разделить на две группы: факторные и результативные. Факторными называются признаки, под воздействием которых изменяются другие признаки - они и образуют группу результативных признаков. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает среднее значение признака результативного. Например: производительность труда зависит от технического уровня предприятия: чем он выше, тем при прочих равных условиях выше производительность труда занятых на предприятии. 36. Коэф детерминации и его значение R2 -коэф-т детерминации.Он выражает долю факторной дисперсии в общей дисперсии, т.е. характеризует,какая часть общей вариации результативного признака y объясняется изучаемым фактором x.Коэф детерминации показ-ет, какой удельный вес влияния среди всех признаков-факторов занимает признак x. 37. Изучение взаимосвязи графич методом Может использоваться как самостоятельно, так и совместно с другими методами. Если конкретные данные перенести на график, то полученное изображение называется полем корреляции. На оси абсцисс откладывается значение факторного признака, а на оси ординат – результативного. Каждая единица, обладающая определенным значением факторного и результативного признака, обозначается точкой. Беспорядочное расположение говорит об отсутствии связи. Наоборот, чем сильнее связь, тем теснее точки группируются вокруг определенной линии. Сущность графического метода составляет наглядное представление наличия и направления взаимосвязей между признаками. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости. 38. Ранговый коэф корреляции, коэф коррел Фехнера. При наличии количеств признаков исп-ся коэф Фехнера и коэф Спирмена. Коэф Фехнера - мера тесноты связи - отношение разности числа пар совпадающих и несовпадающих пар знаков к сумме этих чисел:
39. Построение паралл рядов и количеств оценка их взаимосвязи Приводится ряд данных по одному признаку и параллельно с ним – по другому признаку, связь с которым предполагается. По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее. Сущность метода приведения параллельных данных заключается в следующем: Исходные данные по признаку X располагаются в порядке возрастания или убывания, а по признаку Y записываются соответствующие им показатели. Путем сопоставления значений X и Y, делается вывод о наличии и направлении зависимости.
40. Пок-ль тесноты связи качеств признаков. При наличии качеств (атрибутивных) признаков рассч-ся: коэф ассоциации, коэф контингенции, коэф сопряж-ти К.Пирсона, коэф сопряж-ти А.Чупрова. Коэф ассоциации
41. Динамич ряды, осн эл-ты и правила их построения. Одной из важнейших задач статистики яв-ся изучение изменений анализируемых пок-лей во времени, т.е. их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов). Ряд динамики – это числовые значения опред стат пок-ля в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).Числовые значения того или иного стат пок-ля, составляющего ряд динамики, называют уровнями ряда и обычно обозначают через y. Первый член ряда y1 называют начальным (базисным) уровнем, а последний yn – конечным. Моменты или периоды времени, к к-ым относятся уровни, обозначают через t. Ряды динамики, как правило, представляют в виде таблицы или графически, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y. Формулы индексов 48. Индексы индивид и сводные Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности. Например, изменение выпуска легковых автомобилей определенной марки. Индивидуальный индекс обозначается i. Сводный индекс отражает изменение по всей совокупности элементов сложного явления, - характеризуют относительное изменение индексируемой величины в целом по сложной совокупности, отдельные элементы которой несоизмеримы в натуральных единицах. Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми, или субиндексами. Например, индексы продукции по отдельным отраслям промышленности. Формулы индексов Например, ИПЦ – индекс потребительских цен. Общее изменение образуется под влиянием изменений цен на отдельные товары. Таким образом, мы имеем ряд отношений:
Эти отношения есть не что иное, как индивидуальные индексы, и сводный индекс представляет собой средний из них: 49. Средние индексы Индексы как средние величины: Индекс физического объема Индекс цен Пааше
d0 – удельный вес стоимости каждого товара в общем стоимостном объеме всех товаров в базисном периоде.
50. Баз и цепные индексы. Постоянные и переменные веса индексов Цепные индексы получают сопоставлением текущих уровней с предшествующим. Базисные получают сопоставлением с уровнем периода принятого за базу сравнения. Агрегатные базисные индексы рассчитываются по отношению к постоянной базе (индексы с постоянными весами), а агрегатные цепные индексы - по отношению к меняющейся базе (индексы с переменными весами). Индексам количественных показателей, как правило, соответствуют постоянные веса, индексам качественных показателей -переменные веса. Индекс фиксированного состава качественных показателей Индекс фиксированного состава показывает изменение в среднем только одного исследуемого качественного показателя при постоянной структуре, т.е.
Индекс переменного состава Индекс переменного состава представляет соотношение двух средних величин изучаемого качественного признака, определяемых как взвешенные величины
Он характеризует общее изменение среднего показателя как вследствие изменения уровня индексируемого показателя, так и изменения структуры в рассматриваемой совокупности. Индекс структурных сдвигов При сопоставлении индексов переменного состава и фиксированного состава определяется индекс структурных сдвигов, который показывает, какое влияние на изменение величины индексируемого показателя оказало изменение в текущем периоде по сравнению с базисным изменение структуры совокупности.
Формулы 1. абсолютный прирост средней величины и ее разложение на факторы
2. абсолютный прирост суммарной абсолютной величины и ее разложение на факторы
Индексы цен Индексы цен могут быть рассчитаны по двум вариантам весов - текущим и базисным:
Различия между можно определить по формуле, выведенной В.И. Борткевичем (1868-1931 г.г.):
где
Основные правила В общем расположении на поле графических образов они размещаются слева направо. При этом масштабные ориентиры графика по горизонтальной шкале, как правило, размещаются от его нижней части. Для вертикальной шкалы масштабные ориентиры обычно размещаются в левой части графика. В график по возможности следует включать исходные данные. Если это нецелесообразно, то исходные данные должны в табличной форме сопровождать график. Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс. Общим требованием графического метода является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки — по вертикальной шкале и читаются снизу вверх. При этом важно, чтобы заголовок графика был бы кратким, но достаточно четко пояснял основное его содержание. Эксцесс распределения Поскольку эксцесс нормального распределения равен 3, показатель эксцесса вычисляется по формуле
Оценка существенности эксцесса Для оценки существенности эксцесса вычисляют показатель его средней квадратической ошибки
Если отношение 55. Норм распред и его хар-ки В 1727 Абрахам де Муавр открыл закон распределения вероятностей, названный законом норм распределения. Разработкой вопросов, относящихся к данному закону, занимались Пьер Лаплас и Карл Гаусс. Общие условия возникновения закона норм распред установил Ляпунов. Норм распред образ-ся, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего влияния. Закон норм распред лежит в основе многих теорем и методов статистики при оценке репрез-ти выборки (расчете ошибки выборки и распространении хар-тик выборки на ген сов-ть); измерении степени тесноты связи и составлении модели регрессии; построении и использовании стат критериев.. Распределение непрерывной случайной величины х называют норм N (х,
Свойства норм распред: · Значения признака имеют тенденцию концентрироваться около точки t = 0, где · Норм кривая симметрична относительно вертик оси. · Значения наблюдений не ограничены по своей величине. · · Изменения величины t характеризует разл типы распред. С колебаниями ср величины, кривая норм распределения будет смещаться по оси абсцисс влево или вправо, тогда как форма кривой останется неизменной. 56. Критерии согласия: Пирсона, Романовского, Ястремского. Для проверки гипотезы о соответствии эмпирич распределения теоретич закону норм распределения исп-ся особые стат показатели - критерии согласия (или критерии соответствия). К ним относятся критерии Пирсона, Колмогорова, Романовского, Ястремского. Критерий согласия Пирсона 57. Критерий согласия Пирсона 58. Коэф-ты ассиметрии и эксцесса. Коэф асимм КА хар-ет асимметричность распределения признака в сов-ти . Пок-ль эксцесса EX представляет собой отклонение вершины эмп распред вверх или вниз («крутость») от вершины кривой норм распред. Асимм распределения: при KA=0 распред считается норм; при КА>0 правосторонняя асимм; при КА<0 левосторонняя асимм; если асимм более 0,5, то независимо от знака она считается значительной; если асимм меньше 0,25, то она считается незначительной. Расчет асимметрии распределения при помощи нормированного момента 3 порядка дает наиболее точный результат Виды выборок. 1) собственно случайная выборка. Напр, лото – бочонки с соответствующими номерами помещаются в мешок, они перем-ся, затем бочонки по одному извл-ся из мешка. Выпавшие номера соответствуют единицам, попавшим в выборку; число номеров равно запланиров объему выборки. Отбор жеребьевкой мб подвержен смещениям, вызванным недостатками техники и др причинами. Более надежен с т.зр объективности отбор по таблице случайных чисел. 2) механическая. Часто исп-ся отбор по к-л схеме (так называемая направленная выборка). Схема отбора принимается такой, чтобы отразить осн св-ва и пропорции ген сов-ти. Простейший способ: по спискам единиц ген сов-ти, составленным так, чтобы упорядочивание единиц было бы не связано с изучаемыми свойствами, проводится механический отбор единиц с шагом, равным N. Напр, выбрать опред вокзал, отсчитать 4 путь справа по ходу отправления поездов, сесть в 3 вагон от локомотива и провести опрос пассажира на каждом четном месте. 3) серийная или гнездовая. Напр, серия в промышленности – конфеты, косметические средства, техника. 4) типическая или районированная. Напр, крупный питомник животных или заповедник, где 15% еноты, 25% медведи, 10% рыси, 10% волки, 25% грызуны, 5% лоси, 10% кабаны, то на 100 животных выборка будет представлена 15-ю енотами, 25 медведями, 10 рысями и т.д. 5) динамическая. Выборка во времени. 6) уравновешенная основана на случайном отборе единиц т.обр, что ср размер к-л количеств признака отобранных единиц (для выборки) равен ср размеру этого же признака для всех единиц сов-ти (для ген сов-ти). Уравновешивание по известному количеств признаку представляет собой один из вар-ов типического районирования. Выборку лучше всего производить посредством процесса замещения. Напр, в магазине обуви 20 пар женских сапог на каблуке и 10 пар женских сапог без каблука, а также 20 пар мужской обуви. В уравновешенной выборке будет представлены 2 пары женских сапог на каблуке, 1 пара сапог без каблука и 2 пары мужской обуви. 7) многоступенчатая. Напр, чтобы провести отбор водителей для изучения проблем по орг-ции дорожного движения крупного города, легче провести сначала отбор по классу автомобиля, потом по рыночной стоимости авто, потом выбрать время суток для опроса, затем респ-та. 8) малая выборка (n<30). Напр, группа учащихся. На практике редко прим-ся один вид выборки в чистом виде, как правило, они комбинируются в целях достижения максимальной репрезентативности и экономии. Ошибки выб наблюдения. Разность между показателями выб и ген сов-тей называется ошибкой выборки – μ.Расчет ошибок выборки позволяет оценить репрезентативность (представительность) выб сов-ти.Ошибки выборки характеризуют возможный предел отклонений выборочной средней и выборочной доли от соответственно средней и доли в ген сов-ти.Ошибки выборочного наблюдения: Ошибки регистрации,Ошибки репрезентативности. Ошибки репрезентативности: Случайные (Средние ошибки, Предельные ошибки) и Системные.
24. Собственно-случайная, средняя и предельная ошибки. Коэф доверия. Ср ошибка выборки всегда присутствует в выб иссл-ях и появ-ся вследствие того, что обследуются не все единицы стат сов-ти, а лишь ее часть. Ср ошибка выборки превращается в предельную ошибку Δ при умножении ее на коэф доверия t, к-ый задается предварительно, исходя из требуемой точности наблюдения. Предельная ошибка позволяет судить об «истинном» размере параметра в ген сов-ти с опред степенью вероятности. | ||||||
|
| Поделиться: |


 - пред ошибка,
- пред ошибка,  - ср ошибка, t – коэф доверия. При типическом и серийном отборе, при расчете ошибки выборки вместо общей дисперсии (σ2) следует использовать среднюю из внутригр дисперсий и межгр дисперсию
- ср ошибка, t – коэф доверия. При типическом и серийном отборе, при расчете ошибки выборки вместо общей дисперсии (σ2) следует использовать среднюю из внутригр дисперсий и межгр дисперсию  , где
, где  - частная дисп i группы, ni – объем i группы.
- частная дисп i группы, ni – объем i группы. , где
, где  ср ошибка выб доли.
ср ошибка выб доли.
 , где
, где  ср ошибка выб доли. Для бесповт
ср ошибка выб доли. Для бесповт  , где
, где 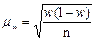 ср ошибка выб доли.
ср ошибка выб доли. Бесповторный отбор:
Бесповторный отбор:  .Предельная ошибка выборки: Δ= t
.Предельная ошибка выборки: Δ= t  . t – коэфициент доверия, зависит от доверительной вероятности, выбранной для исследования. Если t=1, то Δ=ϻ.
. t – коэфициент доверия, зависит от доверительной вероятности, выбранной для исследования. Если t=1, то Δ=ϻ.

 ; для бесповт n =
; для бесповт n = 
 ) значений признака к началу выб набл, как правило, неизвестна, поэтому ее берут приближенно одним из способов: 1) берется из предыд выб набл; 2) по правилу «трех сигм», согласно к-му в размахе вариации укладывается примерно 6 стандартных отклонений
) значений признака к началу выб набл, как правило, неизвестна, поэтому ее берут приближенно одним из способов: 1) берется из предыд выб набл; 2) по правилу «трех сигм», согласно к-му в размахе вариации укладывается примерно 6 стандартных отклонений  ; 3) если приблизительно известна ср величина изучаемого признака, то
; 3) если приблизительно известна ср величина изучаемого признака, то  =
=  2 /9; 4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина
2 /9; 4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина  = 0,25. Ф-лы числ-ти при опред доли Для повт
= 0,25. Ф-лы числ-ти при опред доли Для повт  Для бесповт
Для бесповт 

 ,где С – кол-во совпад знаков отклонений X и У от их средней; Н – кол-во несовпад знаков отклонений от средней. (С+Н=n)Коэф Фехнера не учитывает величину отклонений признаков от ср значений, но он м служить некоторым ориентиром в оценке интенсивности связи. В данном случае он указывает на тесную связь признаков. Ранговый коэф Спирмэна
,где С – кол-во совпад знаков отклонений X и У от их средней; Н – кол-во несовпад знаков отклонений от средней. (С+Н=n)Коэф Фехнера не учитывает величину отклонений признаков от ср значений, но он м служить некоторым ориентиром в оценке интенсивности связи. В данном случае он указывает на тесную связь признаков. Ранговый коэф Спирмэна  где
где  разность рангов по обоим признакам для каждого объекта, i = 1,...,n.
разность рангов по обоим признакам для каждого объекта, i = 1,...,n. , где a,b,c,d- частоты четырехклеточной таблицы.Наличие связи определяется от 0,3. Коэф контингенции
, где a,b,c,d- частоты четырехклеточной таблицы.Наличие связи определяется от 0,3. Коэф контингенции Наличие связи опред-ся от 0,5. Коэф сопряж-ти К.Пирсона
Наличие связи опред-ся от 0,5. Коэф сопряж-ти К.Пирсона 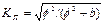 , где φ - сумма квадратов частот каждой строки группы признака, деленных на сумму частот по колонкам и, в свою очередь, на сумму частот по строке без единицы;
, где φ - сумма квадратов частот каждой строки группы признака, деленных на сумму частот по колонкам и, в свою очередь, на сумму частот по строке без единицы;  , где
, где  Коэф сопряж-ти А.Чупрова
Коэф сопряж-ти А.Чупрова , где
, где  число групп по колонкам,
число групп по колонкам,  число групп по строкам.
число групп по строкам. 
 и т.д.
и т.д. , где j - номер товара.
, где j - номер товара.
 Индекс цен Ласпейреса:
Индекс цен Ласпейреса: 

 Форма индекса среднего из индивидуальных адаптирована к практике статистического измерения цен, основанной на выборочных наблюдениях. Выборочные статистические обследования позволяют, во-первых, выяснить, как менялись цены на основные товары и товарные группы. Во-вторых, установить долю каждой товарной группы в общем объеме товаров. Чтобы оценить динамику цен по таким данным формулу Ласпейреса представляют в виде индекса среднего из индивидуальных.
Форма индекса среднего из индивидуальных адаптирована к практике статистического измерения цен, основанной на выборочных наблюдениях. Выборочные статистические обследования позволяют, во-первых, выяснить, как менялись цены на основные товары и товарные группы. Во-вторых, установить долю каждой товарной группы в общем объеме товаров. Чтобы оценить динамику цен по таким данным формулу Ласпейреса представляют в виде индекса среднего из индивидуальных. , где - индекс (темп прироста), характеризующий изменение цены на каждый отдельный товар (индивидуальный индекс).
, где - индекс (темп прироста), характеризующий изменение цены на каждый отдельный товар (индивидуальный индекс).
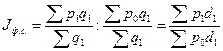
 , где
, где  -доля
-доля
 ,
,  и
и  позволяют определить абсолютные характеристика:
позволяют определить абсолютные характеристика:



 и
и 

 - коэффициент корреляции,
- коэффициент корреляции, - коэффициенты вариации индивидуальных темпов изменения объема и цен
- коэффициенты вариации индивидуальных темпов изменения объема и цен

 - нормированный момент четвертого порядка
- нормированный момент четвертого порядка
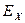 >0 – высоковершинный эксцесс распределения
>0 – высоковершинный эксцесс распределения
 имеет значение больше 3, то это свидетельствует о существенном характере эксцесса
имеет значение больше 3, то это свидетельствует о существенном характере эксцесса

 яв-ся нормиров откл-ем.
яв-ся нормиров откл-ем. ,
,  и
и  имеют одно и то же значение при t = 0.
имеют одно и то же значение при t = 0. где m – частота эмп распределения, m' - частота теорет распред. Табличное значение хи-квадрат опр-ся при пом числа k - числа степеней свободы, равного разности между числом групп (r) и величиной 3 для выравнивания по закону норм распр-я, т.е. k = r-3. Если
где m – частота эмп распределения, m' - частота теорет распред. Табличное значение хи-квадрат опр-ся при пом числа k - числа степеней свободы, равного разности между числом групп (r) и величиной 3 для выравнивания по закону норм распр-я, т.е. k = r-3. Если  ,то расхождения между теорет и факт распр-ем считается неслучайным. Если
,то расхождения между теорет и факт распр-ем считается неслучайным. Если  , то расхождения между теорет и факт распределением считается случайным, а распределение хорошо согласуется с з-м норм распр-ия. Критерий согласия Романовского
, то расхождения между теорет и факт распределением считается случайным, а распределение хорошо согласуется с з-м норм распр-ия. Критерий согласия Романовского  где k - число степеней свободы. Если R<3, расхождения между теорет и эмп частотами считаются случайными. Если R>3, то неслучайными, существенными. Критерии согласия Пирсона и романовского не показывают, чем конкретно отл-ся рассматриваемые распределения. С этой целью применяются спец пок-ли асимметрии и эксцесса. Критерий согласия Ястремского
где k - число степеней свободы. Если R<3, расхождения между теорет и эмп частотами считаются случайными. Если R>3, то неслучайными, существенными. Критерии согласия Пирсона и романовского не показывают, чем конкретно отл-ся рассматриваемые распределения. С этой целью применяются спец пок-ли асимметрии и эксцесса. Критерий согласия Ястремского  где r - число групп. Величина
где r - число групп. Величина  имеет табличное значение, равное 0,6 для распределений, где число групп представлено до 20. Если
имеет табличное значение, равное 0,6 для распределений, где число групп представлено до 20. Если  , расхождение между теорет и эмп распределениями считаются случайными. Если
, расхождение между теорет и эмп распределениями считаются случайными. Если  , расхождение между теорет и эмп распределениями неслучайны, т.е. эмп распределение не отвечает требованиям норм распределения. Критерий согласия Колмогорова
, расхождение между теорет и эмп распределениями неслучайны, т.е. эмп распределение не отвечает требованиям норм распределения. Критерий согласия Колмогорова  Вероятность Р(
Вероятность Р( ) может изменяться от 0 до 1. Если
) может изменяться от 0 до 1. Если  , т.е.
, т.е.  нормированный момент третьего порядка. Для оценки существенности асимметрии вычисляют пок-ль ср квадратич ошибки коэф асимметрии.
нормированный момент третьего порядка. Для оценки существенности асимметрии вычисляют пок-ль ср квадратич ошибки коэф асимметрии.  Если отношение
Если отношение  имеет значение больше 2, то это свидетельствует о существенном хар-ре асимм. Эксцесс распределения. Пок-ль эксцесса ЕХ представляет собой отклонение вершины эмп распред вверх или вниз («крутость») от вершины кривой норм распред, НО! график распределения может выглядеть сколь угодно крутым в зав-ти от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Поскольку эксцесс норм распред равен 3, пок-ль эксцесса вычисляется по ф-ле
имеет значение больше 2, то это свидетельствует о существенном хар-ре асимм. Эксцесс распределения. Пок-ль эксцесса ЕХ представляет собой отклонение вершины эмп распред вверх или вниз («крутость») от вершины кривой норм распред, НО! график распределения может выглядеть сколь угодно крутым в зав-ти от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Поскольку эксцесс норм распред равен 3, пок-ль эксцесса вычисляется по ф-ле  или
или  где
где  нормированный момент 4 порядка. При ЕХ>0 высоковершинный эксцесс распред. При ЕХ<0 низковершинный. При ЕХ=0 норм распред. Для оценки существенности эксцесса вычисляют пок-ль его ср квадратич ошибки
нормированный момент 4 порядка. При ЕХ>0 высоковершинный эксцесс распред. При ЕХ<0 низковершинный. При ЕХ=0 норм распред. Для оценки существенности эксцесса вычисляют пок-ль его ср квадратич ошибки  Если отношение
Если отношение  имеет значение больше 3, то это свидетельствует о существенном характере эксцесса.
имеет значение больше 3, то это свидетельствует о существенном характере эксцесса.


