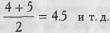Подсчет критерия Q Розенбаума

1. Проверить, выполняются ли ограничения: n₁•n₂ ≥11, n₁ n₂≈n₂ Упорядочить значения отдельно в каждой выборке по степени воз­растания признака. Считать выборкой 1 ту выборку, значения в ко­торой предположительно выше, а выборкой 2 - ту, где значения предположительно ниже.

3. Определить самое высокое (максимальное) значение в выборке 2.

4. Подсчитать количество значений в выборке 1, которые выше макси­мального значения в выборке 2. Обозначить полученную величину как S₁.

5. Определить самое низкое (минимальное) значение в выборке 1.

6. Подсчитать количество значений в выборке 2, которые ниже мини­мального значения выборки 1. Обозначить полученную величину как S₂.

7. Подсчитать эмпирическое значение Q по формуле: Q=S₁+S2-

8. По Табл. I Приложения I определить критические значения Q для данных n₁ и n₂. Если Q_эмп равно Q_0,05 или превышает его, Н₀ от­вергается.

9. При n₁•n₂ >26сопоставить полученное эмпирическое значение с Q_{кp =} 8 (р≤ 0,05) и Q_{кp =} 10(p≤ 0,01). Если Q_эмп превышает или по крайней мере равняется Q_{кp =} 8, H₀ отвергается.

2.3. U - критерий Манна-Уитни

Назначение критерия

Критерий предназначен для оценки различий между двумя вы­борками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n₁•n₂≥ 3 или n₁=2, n₂≥5, и является более мощным, чем критерий Ро­зенбаума.

Описание критерия

Существует несколько способов использования критерия и не­сколько вариантов таблиц критических значений, соответствующих этим способам (Гублер Е. В., 1978; Рунион Р., 1982; Захаров В. П., 1985; McCall R., 1970; Krauth J., 1988).

Этот метод определяет, достаточно ли мала зона перекрещиваю­щихся значений между двумя рядами. Мы помним, что 1-м рядом (выборкой, группой) мы называем тот ряд значений, в котором значе­ния, по предварительной оценке, выше, а 2-м рядом - тот, где они предположительно ниже.

Чем меньше область перекрещивающихся значений, тем более ве­роятно, что различия достоверны. Иногда эти различия называют раз­личиями в расположении двух выборок (Welkowitz J. et al., 1982).

Эмпирическое значение критерия U отражает то, насколько вели­ка зона совпадения между рядами. Поэтому чем меньше U_эмп, тем более вероятно, что различия достоверны.

Гипотезы

Н₀: Уровень признака в группе 2 не ниже уровня признака в группе 1.

H₁: Уровень признака в группе 2 ниже уровня признака в группе 1.

Графическое представление критерия U

На Рис. 2.5. представлены три из множества возможных вариан­тов соотношения двух рядов значений.

В варианте (а) второй ряд ниже первого, и ряды почти не пере­крещиваются. Область наложения слишком мала, чтобы скрадывать различия между рядами. Есть шанс, что различия между ними досто­верны. Точно определить это мы сможем с помощью критерия U.

В варианте (б) второй ряд тоже ниже первого, но и область пе­рекрещивающихся значений у двух рядов достаточно обширна. Она может еще не достигать критической величины, когда различия придет­ся признать несущественными. Но так ли это, можно определить толь­ко путем точного подсчета критерия U.

В варианте (в) второй ряд ниже первого, но область наложения настолько обширна, что различия между рядами скрадываются.

Ограничения критерия U

1. В каждой выборке должно быть не менее 3 наблюдений: n₁•n₂≥3; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.

2. В каждой выборке должно быть не более 60 наблюдений; n₁•n₂≤60. Однако уже при n₁•n₂>20 ранжирование становиться достаточно трудоемким.

На наш взгляд, в случае, если n₁•n₂>20, лучше использовать другой критерий, а именно угловое преобразование Фишера в комбина­ции с критерием λ,, позволяющим выявить критическую точку, в кото­рой накапливаются максимальные различия между двумя сопоставляе­мыми выборками (см. п. 5.4)..Формулировка звучит сложно, но сам метод достаточно прост. Каждому исследователю лучше попробовать разные пути и выбрать тот, который кажется ему более подходящим.

Пример

Вернемся к результатам обследования студентов физического и психологического факультетов Ленинградского университета с помощью методики Д. Векслера для измерения вербального и невербального ин­теллекта. С помощью критерия Q Розенбаума мы в предыдущем па­раграфе смогли с высоким уровнем значимости определить, что уровень вербального интеллекта в выборке студентов физического факультета выше. Попытаемся установить теперь, воспроизводится ли этот резуль­тат при сопоставлении выборок по уровню невербального интеллекта. Данные приведены в Табл. 2.3.

Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?

Таблица 2.3

Индивидуальные значения невербального интеллекта в выборках студентов физического (щ=\4) и психологического (п2⁼12) факультетов

	Студенты-физики		Студенты-психологи
Код имени испытуемого	Показатель невербального интеллекта	Код имени испытуемого	Показатель невербального интеллекта
1.	И.А.		1.	Н.Т.	ИЗ
2.	К.А.		2.	О.В.
3.	К.Е.		3.	Е.В.
4.	П.А.		4.	Ф.О.
5.	С.А.		5.	И.Н.
6.	Ст.А.		6.	И.Ч.
7.	Т.А.		7.	И.В.
8.	Ф.А.		8.	К.О.
9.	Ч.И.		9.	P.P.
10.	ЦА.		10.	Р.И.
11.	См.А.		11.	O.K.
12.	К.Ан.		12.	Н.К.
13.	Б.Л.
14.	Ф.В.

Критерий U требует тщательности и внимания. Прежде всего, необходимо помнить правила ранжирования.

 

Правила ранжирования

1. Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1.

Наибольшему значению начисляется ранг, соответствующий количе­ству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех слу­чаев, которые предусмотрены правилом 2.

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.

Например, 3 наименьших значения равны 10 секундам. Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2 сек; 10,5 сек; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получа­ет средний ранг:

Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:

3. Общая сумма рангов должна совпадать с расчетной, которая опре­деляется по формуле:

где N - общее количество ранжируемых наблюдений (значений). Несовпадение реальной и расчетной сумм рангов будет свидетельст­вовать об ошибке, допущенной при начислении рангов или их сум­мировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

При подсчете критерия U легче всего сразу приучить себя дейст­вовать по строгому алгоритму.

АЛГОРИТМ 4