Как читать эту книгу и как ею пользоваться

СОДЕРЖАНИЕ

Предисловие автора.............. 5

Как читать эту книгу и как ею пользоваться...... 10

Глава 1. Основные понятия, используемые в математической обработке психологических данных........ 11

1.1. Признаки и переменные.......... 11

1.2. Шкалы измерения............. 12

1.3. Распределение признака. Параметры распределения.. 20

1.4. Статистические гипотезы........... 24

1.5. Статистические критерии........... 25

1.6. Уровни статистической достоверности....... 29

1.7. Мощность критериев............ 32

1.8. Классификация задач и методов их решения..... 33

1.9. Принятие решения о выборе метода математической обработки................. 35

1.10. Список обозначений............ 37

Глава 2. Выявление различий в уровне исследуемого признака 39

2.1. Обоснование задачи сопоставления и сравнения.... 39

2.2. Q - критерий Розенбаума........... 42

2.3. U - критерий Манна-Уитни.......... 49

2.4. Н - критерий Крускала-Уоллиса......•.. 56

2.5. S - критерий тенденций Джонкира........ 61

2.6. Задачи для самостоятельной работы....... 69

2.7. Алгоритм принятия решения о выборе критерия для сопоставлений................ 71

Глава 3. Оценка достоверности сдвига в значениях исследуемого признака.............. 72

3.1. Обоснование задачи исследования изменений..... 72

3.2. G - критерий знаков............ 77

3.3. Т - критерий Вилкоксона........... 87

3.4. Критерий х²_г Фридмана........... 94

3.5. L - критерий тенденций Пейджа........ 101

3.6. Задачи для самостоятельной работы....... 107

3.7. Алгоритм принятия решения о выборке критерия оценки изменений................. 109

Глава 4. Выявление различий в распределении признака.. 110

4.1. Обоснование задачи сравнения распределений признака. НО

4.2. X² - критерий Пирсона........... 113

4.3. X - критерий Колмогорова-Смирнова....... 142

4.4. Задачи для самостоятельной работы....... 152

Алгоритм выбора критерия для сравнения распределений... 156

Глава 5. Многофункциональные статистические критерии. 157

5.1. Понятие многофункциональных критериев...... 157

5.2. Критерий ф* - угловое преобразование Фишера... 158

5.3. Биномиальный критерий m.......... 177

5.4. Многофункциональные критерии как эффективные заменители традиционных критериев......... 187

5.5. Задачи для самостоятельной работы....... 194

5.6. Алгоритм выбора многофункциональных критериев... 197

5.7. Математическое сопровождение к описанию критерия ф* Фишера................. 198

Глава 6. Метод ранговой корреляции........ 200

6.1. Обоснование задачи исследования согласованных изменений 200

6.2. Коэффициент ранговой корреляции r_s Спирмена... 208

Глава 7. Дисперсионный анализ.......... 224

7.1. Понятие дисперсионного анализа........ 224

7.2. Подготовка данных к дисперсионному анализу.... 229

7.3. Однофакторный дисперсионный анализ для несвязанных выборок.................. 235

7.4. Однофакторкый дисперсионный анализ для связанных выборок.................. 240

Глава 8. Дисперсионный двухфакторный анализ..... 246

8.1. Обоснование задачи по оценке взаимодействиях двух факторов.................•. 246

8.2. Двухфакторный дисперсионный анализ для несвязанных выборок................... 248

8.3. Двухфакторный дисперсионный анализ для связанных выборок.................. 253

Глава 9. Решения задач с комментариями....... 261

9.1. Рекомендации по решению задач.......• 261

9.2. Решения задач Главы 2........... 261

9.3. Решения задач Главы 3........... 270

9.4. Решения задач Главы 4........... 284

9.5. Решения задач Главы 5........... 301

Заключение................. 308

Библиография................. 309

Приложение 1. Таблицы критических значений..... 315

Приложение 2. Рекомендуемая литература....... 347

ПРЕДИСЛОВИЕ АВТОРА

Принято считать, что математика - это царица наук, и любая наука становится по-настоящему наукой, только когда она начинает ис­пользовать математику. Однако многие психологи в глубине души уве­рены, что царица наук - отнюдь не математика, а психология. Может быть, это скорее два независимых царства, существующих как парал­лельные миры? Математику для доказательства своих положений со­вершенно не требуется привлекать психологию, а психологу можно со­вершать открытия, не привлекая математики. Большинство теорий лич­ности и психотерапевтических концепций были сформулированы безо всякого обращения к математике. Примером могут служить теория пси­хоанализа, бихевиоральная концепция, аналитическая психология К. Юнга, индивидуальная психология А. Адлера, объективная психология В.М. Бехтерева, культурно-историческая теория Л.С. Выготского, кон­цепция отношений личности В. Н. Мясищева и многие другие теории.

Но все это было, в основном, в прошлом. Многие психологиче­ские концепции ныне подвергаются сомнению на основании того, что они не были подтверждены статистически. Стало принято использовать математические методы, как принято жениться молодому человеку, если он хочет сделать дипломатическую или политическую карьеру, и выхо­дить замуж молодой девушке, чтобы доказать, что она может сделать это не хуже, чем все остальные. Но как не всякий молодой человек женится и не всякая девушка выходит замуж, так и не всякое психоло­гическое исследование "венчается" с математикой.

"Брак" психологии с математикой - это брак по принуждению или недоразумению. "Глубокое внутреннее родство, общность происхо­ждения современной физики и современной математики привели к опас­ному..." представлению о том, что всякое явление обязано иметь матема­тическую модель. Это представление тем опаснее, что оно часто счита­ется само собой разумеющимся" (A.M. Молчанов, 1978, с.4).

Психология - это невеста без приданого, у которой нет ни своих собственных единиц измерения, ни отчетливого представления о том, как заимствованные ею единицы измерения - миллиметры, секунды и градусы - соотносятся с психическими феноменами. Эти единицы изме­рения она взяла напрокат у физики, как отчаявшаяся бедная невеста берет взаймы подвенечное платье у более обеспеченной подруги, лишь бы царственный старец взял ее себе в младшие жены.

Между тем, "...явления, составляющие предмет гуманитарных на­ук, неизмеримо сложнее тех, которыми занимаются точные. Они гораз­до труднее (если вообще) поддаются формализации... Вербальный спо­соб построения исследования здесь, как это ни парадоксально, оказыва­ется точнее формально-логического" (И. Грекова, 1976, с.107).

Но каковы эти вербальные способы? Какой иной язык может предложить психология вместо уже ставшего привычным языка сред­них, стандартных отклонений, статистически значимых различий и фак­торных весов? Этой задачи психология пока не решила. Уникальная специфика психологического исследования пока все еще сводится к тра­диционному приписыванию рангов и чисел явлениям, столь тонким, не­уловимым и динамичным, что, по-видимому, к ним применима лишь принципиально иная система регистрации и оценки. Психология отчасти сама виновата в том, что ее заставляют вступать в неравный брак с математикой. Она не смогла пока еще доказать, что строится на прин­ципиально иных основах.

Но пока психология не докажет, что может существовать незави­симо от математики, развод невозможен. Нам придется использовать математические методы, чтобы избавиться от необходимости объяснять, а почему мы, собственно, их не использовали? Легче использовать их, чем доказать, что в этом не было необходимости. Если же мы исполь­зуем их, то целесообразно извлечь из этого максимум пользы. В любом случае, математика, несомненно, систематизирует мышление и позволяет выявить закономерности, на первый взгляд не всегда очевидные.

Ленинградская-Петербургская школа психологии, быть может, более всех других отечественных школ ориентирована на извлечение максимальной пользы из союза психологии с математикой. В 1981 году на Школе молодых ученых в Минске ленинградцы снисходительно улыбались москвичам ("Опять на одном испытуемом закономерность выстраивают!"), а москвичи - ленинградцам ("Опять своими каракати­цами[1] все запутали!").

Автор этой книги принадлежит к Ленинградской психологической школе. Поэтому с первых шагов в психологии я прилежно вычисляла сиг­мы и подсчитывала корреляции, включала разные комбинации признаков в факторный анализ и потом ломала голову над интерпретацией факторов, обсчитывала бесконечное количество дисперсионных комплексов и др. Эти поиски продолжаются вот уже более двадцати лет. За это время я пришла к выводу, что чем проще методы математической обработки и чем ближе они к реально полученным эмпирическим данным, тем более надежными и осмысленными получаются результаты. Факторный и таксономический анализ уже слишком сложны и запутанны, чтобы каждый исследователь мог точно понимать, какие преобразования стоят за ними. Он лишь вво­дит свои данные в "черный ящик", а затем получает ленты машинной вы­дачи с факторными весами признаков, группировками испытуемых и т.д. Далее начинается интерпретация полученных факторов или классифика­ций, и, как любая интерпретация, она неизбежно субъективна. Но ведь субъективно судить о психических феноменах мы можем и безо всяких измерений и вычислений. Интерпретации результатов сложных обсчетов несут в себе лишь видимость научной объективности, поскольку мы по-прежнему субъективно интерпретируем, но уже не реальные результаты наблюдений, а результаты их математической обработки. По этой причи­не факторный, дискриминантный, кластерный, таксономический виды анализа не рассматриваются мною в этой книге.

Принцип отбора методов в данном руководстве - простота и практичность. Большинство методов построены на понятных для иссле­дователя преобразованиях. Некоторые из них ранее редко использова­лись или не использовались совсем - например, критерий тенденций S Джонкира и L Пейджа. Они могут рассматриваться как эффективная замена метода линейной корреляции.

Большинство рассматриваемых методов являются непараметриче­скими, или "свободными от распределения", что значительно расширяет их возможности по сравнению с традиционными параметрическими ме­тодами, например t - критерием Стьюдента и методом линейной корре­ляции Пирсона. Некоторые из предлагаемых методов могут быть при­менены по отношению к любым данным, имеющим хоть какое-то чи­словое выражение. Принцип каждого метода иллюстрируется графиче­ски, с тем, чтобы всякий раз исследователь отчетливо осознавал, какого рода преобразования он совершает.

Все методы рассматриваются на примерах, полученных в реальных психологических исследованиях. К Главам 2-5 прилагаются задачи для самостоятельной работы, решение которых подробно рассматривается в Главе 9.

Все представленные экспериментальные результаты могут ис­пользоваться для научных сопоставлений, так как это реальные научные данные, полученные мною в собственных исследованиях, в совместных исследованиях с моими коллегами или моими учениками.

Применение реальных данных позволяет избежать тех несообраз­ностей, которые часто возникают при рассмотрении искусственно при­думанных задач. Принцип реальности позволяет по-настоящему почув­ствовать подводные камни и тонкости в использовании статистических методов и интерпретации полученных результатов.

Выражаю глубокую признательность людям, без встречи с кото­рыми эта книга не была бы написана. Прежде всего - моим учителям в области математики и математической статистики, Инне Леонидовне Улитиной и профессору Геннадию Владимировичу Суходольскому, благодаря которым использование математики стало для меня скорее удовольствием, чем неприятной обязанностью.

Погрузиться в таинственный мир психологического эксперимента и почувствовать "вкус" к поиску статистических закономерностей мне помогли в юности мои старшие коллеги по Лаборатории антропологии и дифференциальной психологии имени академика Б.Г. Ананьева: Мария Дмитриевна Дворяшина, Борис Степанович Одерышев, Владимир Константинович Горбачевский, Людмила Николаевна Кулешова, Иосиф Маркович Палей, Галина Ивановна Акинщикова, Елена Федоровна Рыбалко, Нина Альбертовна Грищенко-Розе, Лариса Арсеньевна Го-ловей, Николай Николаевич Обозов, Нина Михайловна Владимирова, Ольга Михайловна Анисимова, позже, уже в Лаборатории эксперимен­тальной и прикладной психологии - Капитолина Дмитриевна Шафран-ская.

Все эти люди были влюблены в психологию. Увлеченно и страстно они старались проникнуть в суть того, что проявляется на поверхности человеческих действий и реакций. Воспоминания о совместных поисках и находках неизменно вдохновляли меня при написании этой книги.

Я глубоко благодарна своему научному руководителю по аспиран­туре - декану факультета психологии Санкт-Петербургского универси­тета профессору Альберту Александровичу Крылову - за способность передать мне ощущение гармонии эмпирического материала и за мудрое требование переводить абстрактные математические результаты на язык графических образов, возвращающих к исследуемой реальности.

В разные годы мне очень помогли своими математическими со­ветами психологи: Аркадий Ильич Нафтульев и Наталия Марковна Лебедева, - и математики: Владимир Филиппович Федоров, Михаил Александрович Скороденок, Ярослав Александрович Бедров, Вячеслав Леонидович Кузнецов, Елена Андреевна Вершинина и математический редактор этого руководства Александр Борисович Алексеев, чьи кон­сультации и поддержка были необходимы, как воздух, при подготовке книги.

Выражаю свою признательность руководителю Вычислительного Центра факультета Михаилу Михайловичу Зиберту и сотрудникам цен­тра - Эльвире Аркадьевне Яковлевой, Татьяне Ивановне Гусевой, Григорию Петровичу Савченко за неоценимую помощь в подготовке программ и обработке моих материалов на протяжение многих лет.

В моем сердце жива благодарность и к тем коллегам, кого уже нет с нами - Надежде Петровне Чумаковой, Виктору Ивановичу Буто­ву, Белле Ефимовне Шустер. Их дружеская поддержка и профессио­нальная помощь были неоценимы.

Я отдаю глубокую дань памяти Евгению Сергеевичу Кузьмину, возглавлявшему кафедру социальной психологии Санкт-Петербургского университета в 1966-1988 годах и разработавшему целостную концепцию теоретической и практической подготовки социальных психологов, в про­грамму которой вошел и лекционно-практический курс "Методы матема­тической обработки в психологических исследованиях". Я благодарна ему за включение меня в свой замечательный коллектив, доброе уважительное отношение ко мне и веру в мои профессиональные возможности.

И, наконец, последнее — по списку, но не по значению. Я глу­боко благодарна нынешнему заведующему кафедрой социальной психо­логии — профессору Анатолию Леонидовичу Свенцицкому — за откры­тость новым идеям и поддержание на кафедре атмосферы свободного поиска, высоких интеллектуальных требований и дружеской поддержки, окрашенной юмором и мягкой иронией. Именно такая среда вдохновля­ет к творчеству.

ГЛАВА 1

ОСНОВНЫЕ ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ

В МАТЕМАТИЧЕСКОЙ ОБРАБОТКЕ

ПСИХОЛОГИЧЕСКИХ ДАННЫХ

Признаки и переменные

Признаки и переменные - это измеряемые психологические явле­ния. Такими явлениями могут быть время решения задачи, количество допущенных ошибок, уровень тревожности, показатель интеллектуаль­ной лабильности, интенсивность агрессивных реакций, угол поворота корпуса в беседе, показатель социометрического статуса и множество других переменных.

Понятия признака и переменной могут использоваться как взаи­мозаменяемые. Они являются наиболее общими. Иногда вместо них используются понятия показателя или уровня, например, уровень на­стойчивости, показатель вербального интеллекта и др. Понятия показа­теля и уровня указывают на то, что признак может быть измерен коли­чественно, так как к ним применимы определения "высокий" или "низкий", например, высокий уровень интеллекта, низкие показатели тревожности и др.

Психологические переменные являются случайными величинами, поскольку заранее неизвестно, какое именно значение они примут.

Математическая обработка - это оперирование со значениями признака, полученными у испытуемых в психологическом исследовании. Такие индивидуальные результаты называют также "наблюдениями", "наблюдаемыми значениями", "вариантами", "датами", "индивидуальны­ми показателями" и др. В психологии чаще всего используются терми­ны "наблюдение" или "наблюдаемое значение".

Значения признака определяются при помощи специальных шкал измерения.

Шкалы измерения

Измерение - это приписывание числовых форм объектам или собы­тиям в соответствии с определенными правилами (Стивене С, 1960, с.60). С.Стивенсом предложена классификация из 4 типов шкал измерения:

1) номинативная, или номинальная, или шкала наименований;

2) порядковая, или ординальная, шкала;

3) интервальная, или шкала равных интервалов;

4) шкала равных отношений.

Номинативная шкала - это шкала, классифицирующая по назва­нию: потеп (лат.) - имя, название. Название же не измеряется количе­ственно, оно лишь позволяет отличить один объект от другого или од­ного субъекта от другого. Номинативная шкала - это способ классифи­кации объектов или субъектов, распределения их по ячейкам классифи­кации.

Простейший случай номинативной шкалы - дихотомическая шка­ла, состоящая всего лишь из двух ячеек, например: "имеет братьев и сестер - единственный ребенок в семье"; "иностранец - соотечествен­ник"; "проголосовал "за" - проголосовал "против"" и т.п.

Признак, который измеряется по дихотомической шкале наимено­ваний, называется альтернативным. Он может принимать всего два значения. При этом исследователь зачастую заинтересован в одном из них, и тогда он говорит, что признак “проявился”, если тот принял ин­тересующее его значение, и что признак “не проявился”, если он при­нял противоположное значение. Например: "Признак леворукости про­явился у 8 испытуемых из 20". В принципе номинативная шкала может состоять из ячеек "признак проявился - признак не проявился.

Более сложный вариант номинативной шкалы - классификация из трех и более ячеек, например: "экстрапунитивные - интрапунитивные -импунитивные реакции" или "выбор кандидатуры А - кандидатуры Б -кандидатуры В - кандидатуры Г" или "старший - средний - младший -единственный ребенок в семье" и др.

Расклассифицировав все объекты, реакции или всех испытуемых по ячейкам классификации, мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек.

Как уже указывалось, наблюдение - это одна зарегистрированная реакция, один совершенный выбор, одно осуществленное действие или результат одного испытуемого.

Допустим, мы определим, что кандидатуру А выбрали 7 испы­туемых, кандидатуру Б - 11, кандидатуру В - 28, а кандидатуру Г -всего 1. Теперь мы можем оперировать этими числами, представляю­щими собой частоты встречаемости разных наименований, то есть час­тоты принятия признаком "выбор" каждого из 4 возможных значений. Далее мы можем сопоставить полученное распределение частот с рав­номерным или каким-то иным распределением.

Таким образом, номинативная шкала позволяет нам подсчитывать частоты встречаемости разных "наименований", или значений признака, и затем работать с этими частотами с помощью математических методов.

Единица измерения, которой мы при этом оперируем - количест­во наблюдений (испытуемых, реакций, выборов и т. п.), или частота. Точнее, единица измерения - это одно наблюдение. Такие данные могут быть обработаны с помощью метода χ², биномиального критерия m и углового преобразования Фишера φ*.

Порядковая шкала - это шкала, классифицирующая по принци­пу "больше - меньше". Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные ячейки, то в по­рядковой шкале они образуют последовательность от ячейки "самое ма­лое значение" к ячейке "самое большое значение" (или наоборот). Ячейки теперь уместнее называть классами, поскольку по отношению к классам употребимы определения "низкий", "средний" и "высокий" класс, или 1-й, 2-й, 3-й класс, и т.д.

В порядковой шкале должно быть не менее трех классов, напри­мер "положительная реакция - нейтральная реакция - отрицательная реакция" или "подходит для занятия вакантной должности - подходит с оговорками - не подходит" и т. п.

В порядковой шкале мы не знаем истинного расстояния между классами, а знаем лишь, что они образуют последовательность. Напри­мер, классы "подходит для занятия вакантной должности" и "подходит с оговорками" могут быть реально ближе друг к другу, чем класс "подходит с оговорками" к классу "не подходит".

От классов легко перейти к числам, если мы условимся считать, что низший класс получает ранг 1, средний класс - ранг 2, а высший класс - ранг 3, или наоборот. Чем больше классов в шкале, тем больше у нас возможностей для математической обработки полученных данных и проверки статистических гипотез.

Например, мы можем оценить различия между двумя выборками испытуемых по преобладанию у них более высоких или более низких рангов или подсчитать коэффициент ранговой корреляции между двумя переменными, измеренными в порядковой шкале, допустим, между оценками профессиональной компетентности руководителя, данными ему разными экспертами.

Все психологические методы, использующие ранжирование, по­строены на применении шкалы порядка. Если испытуемому предлагает­ся упорядочить 18 ценностей по степени их значимости для него, проранжировать список личностных качеств социального работника или 10 претендентов на эту должность по степени их профессиональной при­годности, то во всех этих случаях испытуемый совершает так называе­мое принудительное ранжирование, при котором количество рангов со­ответствует количеству ранжируемых субъектов или объектов (ценностей, качеств и т.п.).

Независимо от того, приписываем ли мы каждому качеству или испытуемому один из 3-4 рангов или совершаем процедуру принуди­тельного ранжирования, мы получаем в обоих случаях ряды значений, измеренные по порядковой шкале. Правда, если у нас всего 3 возмож­ных класса и, следовательно, 3 ранга, и при этом, скажем, 20 ранжи­руемых испытуемых, то некоторые из них неизбежно получат одинако­вые ранги. Все многообразие жизни не может уместиться в 3 градации, поэтому в один и тот же класс могут попасть люди, достаточно серьез­но различающиеся между собой. С другой стороны, принудительное ранжирование, то есть образование последовательности из многих ис­пытуемых, может искусственно преувеличивать различия между людь­ми. Кроме того, данные, полученные в разных группах, могут оказаться несопоставимыми, так как группы могут изначально различаться по уровню развития исследуемого качества, и испытуемый, получивший в одной группе высший ранг, в другой получил бы всего лишь средний, и т.п.

Выход из положения может быть найден, если задавать доста­точно дробную классификационную систему, скажем, из 10 классов, или градаций, признака. В сущности, подавляющее большинство психологи­ческих методик, использующих экспертную оценку, построено на изме­рении одним и тем же "аршином" из 10, 20 или даже 100 градаций разных испытуемых в разных выборках.

Итак, единица измерения в шкале порядка - расстояние в 1 класс или в 1 ранг, при этом расстояние между классами и рангами может быть разным (оно нам неизвестно). К данным, полученным по поряд­ковой шкале, применимы все описанные в данной книге критерии и ме­тоды.

Интервальная шкала - это шкала, классифицирующая по прин­ципу "больше на определенное количество единиц - меньше на опреде­ленное количество единиц". Каждое из возможных значений признака отстоит от другого на равном расстоянии.

Можно предположить, что если мы измеряем время решения за­дачи в секундах, то это уже явно шкала интервалов. Однако на самом деле это не так, поскольку психологически различие в 20 секунд между испытуемым А и Б может быть отнюдь не равно различию в 20 се­кунд между испытуемыми Б и Г, если испытуемый А решил задачу за 2 секунды, Б - за 22, В - за 222, а Г - за 242.

Аналогичным образом, каждая секунда после истечения полутора минут в опыте с измерением мышечного волевого усилия на динамомет­ре с подвижной стрелкой, по "цене", может быть, равна 10 или даже более секундам в первые полминуты опыта. "Одна секунда за год идет" - так сформулировал это однажды один испытуемый.

Попытки измерять психологические явления в физических едини­цах - волю в секундах, способности в сантиметрах, а ощущение собст­венной недостаточности - в миллиметрах и т. п., конечно, понятны, ведь все-таки это измерения в единицах "объективно" существующего времени и пространства. Однако ни один опытный исследователь при этом не обольщает себя мыслью, что он совершает измерения по психо­логической интервальной шкале. Эти измерения принадлежат по-прежнему к шкале порядка, нравится нам это или нет (Стивене С, 1960, с.56; Паповян С.С., 1983, с.63; Михеев В.И.: 1986, с.28).

Мы можем с определенной долей уверенности утверждать лишь, что испытуемый А решил задачу быстрее Б, Б быстрее В, а В быстрее Г.

Аналогичным образом, значения, полученные испытуемыми в баллах по любой нестандартизованной методике, оказываются измерен­ными лишь по шкале порядка. На самом деле равноинтервальными можно считать лишь шкалы в единицах стандартного отклонения и про-центильные шкалы, и то лишь при условии, что распределение значений в стандартизующей выборке было нормальным (Бурлачук Л. Ф., Мо­розов С. М., 1989, с. 163, с. 101).

Принцип построения большинства интервальных шкал построен на известном правиле "трех сигм": примерно 97,7-97,8% всех значений признака при нормальном его распределении укладываются в диапазоне М±3σ[2] Можно построить шкалу в единицах долей стандартного откло­нения, которая будет охватывать весь возможный диапазон изменения признака, если крайний слева и крайний справа интервалы оставить открытыми.

Р.Б. Кеттелл предложил, например, шкалу стенов - "стандартной десятки". Среднее арифметическое значение в "сырых" баллах прини­мается за точку отсчета. Вправо и влево отмеряются интервалы, равные 1/2 стандартного отклонения. На Рис. 1.2 представлена схема вычисле­ния стандартных оценок и перевода "сырых" баллов в стены по шкале N 16-факторного личностного опросника Р. Б. Кеттелла.

Справа от среднего значения будут располагаться интервалы, равные 6, 7, 8, 9 и 10 стенам, причем последний из этих интервалов открыт. Слева от среднего значе­ния будут располагаться интервалы, равные 5, 4, 3, 2 и 1 стенам, и крайний интервал также открыт. Теперь мы поднимаемся вверх, к оси "сырых баллов", и размечаем границы интервалов в единицах "сырых" баллов. Поскольку М=10,2; σ=2,4, вправо мы откладываем 1/2σ, т.е. 1,2 "сырых" балла. Таким образом, гра­ница интервала составит: (10,2 + 1,2) = 11,4 "сырых" балла. Итак, границы ин­тервала, соответствующего 6 стенам, будут простираться от 10,2 до 11,4 баллов. В сущности, в него попадает только одно "сырое" значение - 11 баллов. Влево от средней мы откладываем 1/2 σ и получаем границу интервала: 10,2-1,2=9. Таким образом, границы интервала, соответствующие 9 стенам, простираются от 9 до 10,2. В этот интервал попадают уже два "сырых" значения - 9 и 10. Если испы­туемый получил 9 "сырых" баллов, ему начисляется теперь 5 стенов; если он по­лучил 11 "сырых" баллов - 6 стенов, и т. д.

Мы видим, что в шкале стенов иногда за разное количество "сырых" баллов будет начисляться одинаковое количество стенов. Например, за 16, 17, 18, 19 и 20 баллов будет начисляться 10 стенов, а за 14 и 15 - 9 стенов и т. д.

В принципе,шкалу стенов можно построить по любым данным, измеренным по крайней мере в порядковой шкале, при объеме выборки п>200 и нормальном рас­пределении признака[3].

Другой способ построения равноинтервальной шкалы - группировка интервалов по принципу равенства накопленных частот. При нормальном распределении при­знака в окрестности среднего значения группируется большая часть всех наблюде­ний, поэтому в этой области среднего значения интервалы оказываются меньше, уже, а по мере удаления от центра распределения они увеличиваются, (см. Рис. 1.2). Следовательно, такая процентильная шкала является равноинтервальной толь­ко относительно накопленной частоты (Мельников В.М., Ямпольский Л.Т., 1985, с. 194).

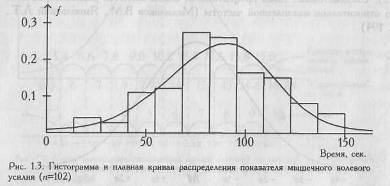
Построение шкал равных интервалов по данным, полученным по шкале порядка, напоминает трюк с веревочной лестницей, на который ссылался С. Стивене. Мы сначала поднимаемся по лестнице, которая ни на чем не закреплена, и добираемся до лестницы, которая закрепле­на. Однако каким путем мы оказались на ней? Измерили некую психо­логическую переменную по шкале порядка, подсчитали средние и стан­дартные отклонения, а затем получили, наконец, интервальную шкалу. "Такому нелегальному использованию статистики может быть дано из­вестное прагматическое оправдание; во многих случаях оно приводит к плодотворным результатам" (Стивене С, 1960, с. 56).

Многие исследователи не проверяют степень совпадения получен­ного ими эмпирического распределения с нормальным распределением, и тем более не переводят получаемые значения в единицы долей стан­дартного отклонения или процентили, предпочитая пользоваться "сырыми" данными. "Сырые" же данные часто дают скошенное, срезан­ное по краям или двухвершинное распределение. На Рис. 1.3 представле­но распределение показателя мышечного волевого усилия на выборке из 102 испытуемых. Распределение с удовлетворительной точностью мож­но считать нормальным (χ²=12,7, при v=9, M=89,75, σ= 25,1).

На Рис. 1.4 представлено распределение показателя самооценки по шкале методики Дж. Менестера - Р.Корзини "Уровень успеха, ко­торого я должен был достичь уже сейчас" (n=356). Распределение зна­чимо отличается от нормального (χ²=58,8, при v=7; p< 0,01; М=80,64; σ =16,86).

С такими "ненормальными" распределениями приходится встре­чаться очень часто, чаще, может быть, чем с классическими нормаль­ными. И дело здесь не в каком-то изъяне, а в самой специфике психо­логических признаков. По некоторым методикам от 10 до 20% испы­туемых получают оценку "ноль" - например, в их рассказах не встреча­ется ни одной словесной формулировки, которая отражала бы мотив "надежда на успех" или "боязнь неудачи" (методика Хекхаузена). То, что испытуемый получил оценку "ноль", нормально, но распределение таких оценок не может быть нормальным, как бы мы ни увеличивали объем выборки (см. п. 5.3).

Методы статистической обработки, предлагаемые в настоящем руководстве, в большинстве своем не требуют проверки совпадения по­лученного эмпирического распределения с нормальным. Они построены на подсчете частот и ранжировании. Проверка необходима только в случае применения дисперсионного анализа. Именно поэтому соответст­вующая глава сопровождается описанием процедуры подсчета необхо­димых критериев.

Во всех остальных случаях нет необходимости проверять степень совпадения полученного эмпирического распределения с нормальным, и тем более стремиться преобразовать порядковую шкалу в равноинтервальную. В каких бы единицах ни были измерены переменные - в се­кундах, миллиметрах, градусах, количестве выборов и т. п. - все эти данные могут быть обработаны с помощь непараметрических критери­ев[4], составляющих основу данного руководства.

Шкала равных отношений - это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности изме­ряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу: 2 так относится к 4, как 4 к 8. Это предполагает наличие абсолютной нулевой точки отсчета. В физике абсолютная нулевая точка отсчета встречается при измерении длин от­резков или физических объектов и при измерении температуры по шка­ле Кельвина с абсолютным нулем температур. Считается, что в психо­логии примерами шкал равных отношений являются шкалы порогов аб­солютной чувствительности (Стивене С, 1960; Гайда В. К., Захаров В. П., 1982). Возможности человеческой психики столь велики, что трудно представить себе абсолютный нуль в какой-либо измеряемой психологической переменной. Абсолютная глупость и абсолютная чест­ность - понятия скорее житейской психологии.

То же относится и к установлению равных отношений: только метафора обыденной речи допускает, чтобы Иванов был в 2 раза (3, 100, 1000) умнее Петрова или наоборот.

Абсолютный нуль, правда, может иметь место при подсчете ко­личества объектов или субъектов. Например, при выборе одной из 3 альтернатив испытуемые не выбрали альтернативу А ни одного раза, альтернативу Б - 14 раз и альтернативу В - 28 раз. В этом случае мы можем утверждать, что альтернативу В выбирают в два раза чаще, чем альтернативу Б. Однако при этом измерено не психологическое свойст­во человека, а соотношение выборов у 42 человек.

По отношению к показателям частот возможно применять все арифметические операции: сложение, вычитание, деление и умножение. Единица измерения в этой шкале отношений - 1 наблюдение, 1 выбор, 1 реакция и т. п. Мы вернулись к тому, с чего начали: к универсальной шкале измерения в частотах встречаемости того или иного значения признака и к единице измерения, которая представляет собой 1 наблю­дение. Расклассифицировав испытуемых по ячейкам номинативной шка­лы, мы можем применить потом высшую шкалу измерения - шкалу от­ношений между частотами.

Статистические гипотезы

Формулирование гипотез систематизирует предположения иссле­дователя и представляет их в четком и лаконичном виде. Благодаря гипотезам исследователь не теряет путеводной нити в процессе расчетов и ему легко понять после их окончания, что, собственно, он обнаружил.

Статистические гипотезы подразделяются на нулевые и альтерна­тивные, направленные и ненаправленные.

Нулевая гипотеза - это гипотеза об отсутствии различий. Она обозначается как H₀ и называется нулевой потому, что содержит число 0: X₁- Х₂=0, где X₁, X₂ - сопоставляемые значения признаков.

Нулевая гипотеза - это то, что мы хо­тим опровергнуть, если перед нами стоит задача доказать значимость различий.

Альтернативная гипотеза - это гипотеза о значимости различий. Она обозначается как H₁. Альтернатив­ная гипотеза - это то, что мы хотим до­казать, поэтому иногда ее называют экспериментальной гипотезой.

Бывают задачи, когда мы хотим доказать как раз незначимость различий, то есть подтвердить нулевую гипотезу. Например, если нам нужно убедиться, что разные испытуемые получают хотя и различные, но уравновешенные по трудности задания, или что экспериментальная и контрольная выборки не различаются между собой по каким-то значи­мым характеристикам. Однако чаще нам все-таки требуется доказать значимость различий, ибо они более информативны для нас в поиске нового. Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными.

Направленные гипотезы

H₀: X₁ не превышает Х₂

H₁: X₁ превышает Х₂

Ненаправленные гипотезы

H₀: X₁ не отличается от Х₂

Н₁: Х₁ отличается от Х₂

Если вы заметили, что в одной из групп индивидуальные значе­ния испытуемых по какому-либо признаку, например по социальной смелости, выше, а в другой ниже, то для проверки значимости этих различий нам