
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарный режим автогенератораСодержание книги
Поиск на нашем сайте
Автогенератор переходит в стационарный режим, когда неравенство (12) становится равенством, причем это происходит за счет уменьшения значения коэффициента усиления Ку. Уменьшение Ку с физической точки зрения объясняется следующим. По мере увеличения амплитуды колебаний на контуре автогенератора растет напряжение обратной связи, что приводит к уменьшению средней за период колебаний крутизны АЭ. В результате коэффициент усиления с ростом амплитуды Uк падает. Процессы, происходящие в автогенераторе, описываются нелинейными дифференциальными уравнениями. Точных аналитических решений этих уравнений, как правило, не существует. В связи с этим были разработаны различные методы приближенного анализа нелинейных цепей. Наибольшее распространение получили: квазилинейный метод; метод линеаризации; метод фазовой плоскости; метод малого параметра; метод математического моделирования. Основным инженерным методом анализа является квазилинейный метод. Квазилинейный метод состоит в замене соотношений между токами и напряжениями в схеме соотношениями между их первыми гармониками. Такая замена возможна, т.к. колебательные контуры генераторов имеют высокую добротность (50-200), т.е. обладает большой избирательностью. Из-за нелинейности АЭ колебания на его выходе существенно отличаются от синусоидальных: появляются новые гармонические составляющие. Поскольку контур обладает высокими избирательными свойствами, колебания на его выходе имеют синусоидальный характер. Поэтому напряжение uв, поступающее на вход АЭ совпадают по форме с напряжением uк, снимаемым с колебательного контура, независимо от формы выходного тока АЭ. Таким образом, между колебаниями, поступающими на вход АЭ, и колебаниями на контуре имеется линейная связь. Однако это наблюдается только при фиксированной амплитуде. Между амплитудами колебаний линейной связи нет; эта связь существенно нелинейно. Следовательно, при фиксированных параметрах АЭ и колебательный контур можно рассматривать как линейную систему. Однако нелинейные свойства по отношению к амплитуде колебаний сохраняются: меняется наклон линеаризованной характеристики, т.е. крутизна по первой гармонике - средняя крутизна. Таким образом, нелинейные свойства АЭ отражаются изменением средней крутизны при изменении амплитуды. Амплитуды первых гармоник выходного тока Iк1 и напряжения возбуждения Uв1 связаны соотношением
где
В общем случае величины, входящие в (14), являются комплексными. Для линейной части схемы (при iв1 =0) имеем где (На резонансной частоте Входное напряжение
В стационарном режиме должны одновременно удовлетворяться оба уравнения (14) и (16). Подставляя (16) в (14), получаем комплексное уравнение автогенератора
или
Физический смысл этого выражения: в стационарном режиме комплексный коэффициент передачи по замкнутому контуру генератора равен единице. Если входящие в выражение (17) комплексные величины представить в показательной форме, то уравнение (17) можно записать в виде
где js - сдвиг фаз в АЭ; jос - сдвиг фаз в цепи обратной связи, jz - сдвиг фаз в контуре.
Уравнение (18) имеет место, если одновременно выполняются два условия:
Выражение (19а) называется условием баланса фаз. Оно означает, что в стационарном режиме сумма всех фазовых сдвигов по замкнутому контуру генератора равна нулю или целому числу 2p. Поскольку каждый из сдвигов фаз, входящий в (19а) зависит от частоты по-разному, в большинстве генераторов существует лишь одна частота w, на которой выполняется условие баланса фаз, т.е. на которой возможно генерирование колебаний. Выражение (19б) называется условием баланса амплитуд. Оно означает, что в стационарном режиме коэффициент передачи по замкнутому контуру генератора равен единице. В этом условии величины gос и Zк от амплитуды колебаний не зависят, а величина Sср зависит от Uв1. Следовательно, условие баланса амплитуд выполняется лишь при определенной амплитуде Uв1. Условия баланса амплитуд и фаз должны выполняться для любых схем автогенераторов, в том числе и для импульсных.
14.5 Мягкий и жесткий режим самовозбуждения колебаний В квазилинейном методе для определения амплитуды стационарных колебаний применяется один из двух равноценных методов. Первый из них базируется на характеристиках средней крутизны, второй - на использовании колебательной характеристики. Характер зависимости средней крутизны Sср от амплитуды напряжения Uв1 определяется видом динамической характеристики Колебательной характеристикой называется зависимость амплитуды первой гармоники выходного тока (или напряжения) нелинейного элемента Iк1 от амплитуды входного гармонического напряжения Uв1:
Колебательную характеристику и зависимость При любой амплитуде Uв1 средняя крутизна
где a - угол наклона линии, соединяющей точку колебательной характеристики с началом координат. На рис.6б построена характеристика средней крутизны Если смещение Режим работы генератора с характеристиками 1 называется мягким, а с характеристикой 2 - жестким. Как уже отмечалось, колебательная характеристика может быть получена аналитическим методом, если динамическую характеристику АЭ аппроксимировать относительно рабочей точки полиномом. Можно показать, что при анализе работы генератора в мягком режиме вольт - амперная характеристика его нелинейного элемента должна быть аппроксимирована полиномом не ниже 3-й степени, а в жестком - не ниже 5-й степени. Рассмотрим особенности работы автогенератора в мягком и жестком режимах. Мягкий режим. При мягком режиме самовозбуждения рабочая точка выбирается на участке передаточной характеристике с максимальной крутизной. Для определения амплитуды стационарных колебаний выражение (19б) удобно переписать в виде
Амплитуду стационарных колебаний Uст можно найти графическим путем как точку пересечения графика характеристики средней крутизны На колебательной характеристике амплитуда стационарных колебаний определяется как точка пересечения колебательной характеристики с характеристикой обратной связи. На рис.6а помимо колебательной характеристики
На рис.6а характеристики обратной связи приведены для различных значений M (M1 < M2 < M3 < M4). Стационарным режимам соответствуют точки пересечения колебательной характеристики и характеристики обратной связи. Однако стационарный режим должен быть еще и устойчивым. При M = M3 точек пересечения окажется две: точка О (Uв1 =0) и точка А3, соответствующая динамическому режиму с амплитудой Для определения устойчивости состояния равновесия необходимо выяснить, как ведет себя система при малых отклонениях от него. Точка О является неустойчивой. Предположим, что за счет какого-то возмущения возникло колебание напряжения с небольшой амплитудой D Uв1. Это вызовет появление тока с амплитудой D Iк1, определяемой по колебательной характеристике. В свою очередь этот ток создает напряжение на входе АЭ с амплитудой D Uв2, определяемой по характеристике обратной связи, причем DUв2 > DUв1, что вызовет дальнейшее увеличение тока и т.д. В итоге амплитуда случайно возникшего колебания возрастает, т.е. состояние равновесия оказывается неустойчивым. Аналогично проводится проверка устойчивости точки А3. Легко убедиться при этом, что динамический режим в этой точке является устойчивым, т.к. небольшие отклонения затухают.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.199 (0.007 с.) |

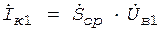 , (14)
, (14) - средняя крутизна АЭ.
- средняя крутизна АЭ. зависит от амплитуды напряжения Uв1.
зависит от амплитуды напряжения Uв1.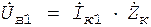 , (15)
, (15) - эквивалентное сопротивление параллельного контура.
- эквивалентное сопротивление параллельного контура. )
)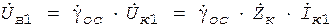 (16)
(16)
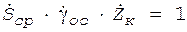 (17)
(17) . (17а)
. (17а) , (18)
, (18) , (n=0,1,2...) (19а)
, (n=0,1,2...) (19а) . (19б)
. (19б) АЭ и положением рабочей точки Ев. Ее можно получить графическим методом или аналитическим методом при аппроксимации характеристики
АЭ и положением рабочей точки Ев. Ее можно получить графическим методом или аналитическим методом при аппроксимации характеристики  , (
, (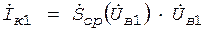 )
) можно определить по динамической вольт - амперной характеристике АЭ (см. рис.5). При выбранном смещении
можно определить по динамической вольт - амперной характеристике АЭ (см. рис.5). При выбранном смещении  для различных амплитуд входного напряжения (
для различных амплитуд входного напряжения ( >
>  >
>  ) строятся графики iк и рассчитываются амплитуды их первых гармоник. Для смещения
) строятся графики iк и рассчитываются амплитуды их первых гармоник. Для смещения  . По мере увеличения амплитуды Uв1 напряжение все более заходит на участокменьшей крутизны, в результате чего рост амплитуды Iк1 замедляется. Соответствующая колебательная характеристика показана на рис.6а (кривая 1).
. По мере увеличения амплитуды Uв1 напряжение все более заходит на участокменьшей крутизны, в результате чего рост амплитуды Iк1 замедляется. Соответствующая колебательная характеристика показана на рис.6а (кривая 1). ,
, , соответствующая колебательной характеристике 1 При малых Uв1 средняя крутизна определяется крутизнойв рабочей точке
, соответствующая колебательной характеристике 1 При малых Uв1 средняя крутизна определяется крутизнойв рабочей точке  . При увеличении амплитуды колебаний средняя крутизна уменьшается.
. При увеличении амплитуды колебаний средняя крутизна уменьшается.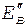 соответствует нижнему загибу характеристики
соответствует нижнему загибу характеристики  .
. .
. , построено семейство характеристик обратной связи, определяющих зависимость Uв1 от Iк1 через линейные элементы генератора. Из уравнения (16) имеем
, построено семейство характеристик обратной связи, определяющих зависимость Uв1 от Iк1 через линейные элементы генератора. Из уравнения (16) имеем . (
. (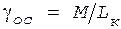 )
) . В каждой из них выполняется условие баланса амплитуд. Однако это еще не означает, что любой из этих режимов может быть получен. В реальных схемах может быть получен только устойчивый режим.
. В каждой из них выполняется условие баланса амплитуд. Однако это еще не означает, что любой из этих режимов может быть получен. В реальных схемах может быть получен только устойчивый режим.


