
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 8. Применение операционных усилителейСодержание книги
Поиск на нашем сайте
ЛЕКЦИЯ 8. ПРИМЕНЕНИЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ 1. Использование операционных усилителей 2. Инвертирующий усилитель 3. Виды реализации фильтров ФНЧ, ФВЧ, ПЗФ, ППФ
Использование операционных усилителей На этой лекции мы рассмотрим аспекты применения разнообразных усилителей. Но главным образом мы будем рассматривать применение ОУ, так как именно они чаще всего используются в современной электронике. Начнём именно с них. Обозначаются операционные усилители так же, как и обычные усилители – треугольником, но у ОУ два входа, и один с инверсией:
Обычно слева два входа, которые различаются наличием или отсутствием кружочка, обозначающего инверсию (иногда внутри треугольника вместо кружочка пишут + и – соответственно у неинвертирующего и инвертирующего входов). Справа обычно обозначается выход ОУ. Иногда на схемах больше ничего нет, но на самом деле есть ещё и питание (+Еп и –Еп), оно обычно обозначается сверху и снизу. Кроме того, у современных ОУ есть ещё и баланс нуля, обычно два провода снизу, и провод для подключения коррекции. Ещё может быть контакт для земли, хотя он редко бывает необходим. Обычно это всё, но может быть и что-то ещё. На реальных схемах вместо слов обычно пишут номера контактов. Как мы видим, на этой схеме всего 8 контактов, вместо 12х3=36 у 12 транзисторов, а у всех элементов порядка 50...100. В этом главное преимущество микроэлектроники, так как надёжность (интенсивность отказов) главным образом определяется именно количеством контактов. Как же сделать схему усилителя на ОУ? Очевидно, надо подать на неинвертирующий вход сигнал, а с выхода часть сигнала подать на инвертирующий вход. Получится схема:
Так как ОУ обладает большим Кос, можно считать, что глубина обратной связи большая, и коэффициент усиления этой схемы равен
Но в данном случае равно падению напряжения на R1, которое возникает из-за протекания тока по цепи Roc-R1:
Следовательно, Это очень важная формула, она говорит, что Кос не зависит от К0 (когда глубина ООС большая), а зависит только от соотношения величин сопротивлений Rос и R1. Такой усилитель называется неинвертирующим. Если Roc=0, или выходной сигнал подаётся прямо на вход, то Кос=1. Это – повторитель сигнала. Его суть состоит в согласовании входных и выходных сопротивлений. Это последовательная связь по напряжению, значит, входное сопротивление очень велико, а выходное – очень мало.
Инвертирующий усилитель
Теперь рассмотрим инвертирующий усилитель (см. на рис.). Нам теперь трудно определить коэффициент обратной связи В. Но можно найти другой способ рассуждения. Как мы видели из предыдущей лекции, при ООС Uвх0=Uвх/F. Даже если Uвх велико, например, 10 В, Uвх0 всё равно очень мало. Пусть F=100, тогда это 0,1 В, а если F=1000, то это всего 10 мВ. Ну а при нормальных входных сигналах, которые обычно малы, например, 0,1 В, Uвх0 вообще мало, и равно 1...0,1 мВ. Обычно считают, что это заземление, хотя никакого заземления нет. Говорят, что на инвертирующем входе "псевдоземля" или что это "виртуальная земля". Причина этого заключается в том, что выходное напряжение не может превышать напряжение питания. Если выходное напряжение должно быть больше, усилитель не работает, так он находится "в зашкале". Напряжение питания обычно 10...30 В, а коэффициент усиления 1000...1000000. Другими словами входное напряжение не должно превышать напряжение 30 мкВ... 30 мВ. Мы можем это считать псевдоземлёй. Теперь давайте рассмотрим протекание тока в точке соединения сопротивлений. Слева втекает входной ток Iвх, справа вытекает ток обратной связи Iос, и ещё возможен ток, протекающий к инвертирующему входу ОУ. Но последний очень мал. Дело в том, что входное сопротивление ОУ обычно высокое, а может быть даже очень высокое, а входное напряжение очень мало. Поэтому этот ток измеряется нано- и даже пикроамперами, и мы можем смело им пренебречь (на рис. этот ток перечёркнут). Итак, есть только два тока: Iвх и Iос. Конечно, они должны быть равны друг другу:
Подставим их значения:
Вспомнив, что Кос=Uвых/Uвх, получим
Итак, мы получили коэффициент усиления с инверсией, что естественно, но на единицу меньше, чем у неинвертирующего усилителя на ОУ. Если Roc=R1, то Кос= -1, то-есть у нас получился инвертор. Последний результат очень важен. То, что у нас есть псевдоземля, значительно упрощает расчёт коэффициента усиления: мы берём входной сигнал (напряжение входа) и делим его на входное сопротивление. Получаем ток, который равен току выхода. Если умножить его на сопротивление обратной связи, то получим выходное напряжение (с минусом). Этот подход легко можно использовать при функциональных преобразованиях. Возьмём, например, вместо входного сопротивления диод:
Тогда входной ток определяется уравнением:
Отбрасывая второе слагаемое I0, так как это малая величина по сравнению с первым, и умножая на Roc, получаем:
Первое слагаемое – константа, а второе с точностью до постоянного множителя RocI0 является как раз экспонентой. Теперь давайте посмотрим, что получится, если диод поставить в другое место, туда, где стоит сопротивление обратной связи:
Теперь выражения для токов будут:
Решив это уравнение относительно Uвых, получим:
То-есть мы получили логарифмирующий усилитель. Можно ли сделать суммирование? Да, это возможно:
Здесь входные токи равны входным напряжениям, делённым на входные сопротивления. Далее эти токи суммируются и приравниваются к выходному току, равному отношению выходного напряжения к сопротивлению обратной связи:
Умножив всё на Roc, получим:
Если все сопротивления одинаковы, формула упрощается:
Есть ещё две интересные схемы с конденсатором вместо входного сопротивления или конденсатором в цепи обратной связи:
Как известно, напряжение на конденсаторе определяется по формуле (для левой схемы):
где Q – заряд конденсатора. Если заряд конденсатора продифференцировать, то получится ток через конденсатор:
Приравнивая это току цепи обратной связи, получим формулу:
На левом рисунке представлены зависимости от времени входного и выходного сигнала. На правом рис. частотная зависимость для дифференцирующего усилителя. Легко понять, что на правом рис. (выше) показан интегратор. Для него графики будут обратными:
Здесь слева показан эффект интегрирования входного сигнала. Справа показана частотная характеристика интегратора. Рассмотренные нами устройства как раз и нужны для создания аналоговой вычислительной машины (АЭВМ). Предположим, нам надо решить уравнение:
интегрирующий усилитель, два простых усилителя с точно заданными коэффициентами усиления для моделирования умножения на постоянные коэффициенты, один сумматор. Схема такой АЭВМ представлена ниже:
Необходимо подключить точку "y" к осциллографу и наблюдать изменение сигнала. Такие АЭВМ получили распространение в 50...60 годы прошлого века. Состояли они из нескольких десятков усилителей, которые как раз и назывались "операционными", так как предназначались для операций, к ним прилагались несколько сот пассивных элементов, и всё это коммутировалось таким образом, чтобы собрать схему для решения конкретного уравнения. Точность каждого операционного усилителя лучше, чем 0,1%. Однако общая точность решения дифференциального уравнения не превышает 1...5%. В настоящее время АЭВМ надёжно ушли в прошлое. А ОУ остались! А теперь давайте рассмотрим некоторые другие применения ОУ. Цифровую технику, где ОУ применяются широко, оставим для второй части электроники. А здесь рассмотрим резонансные усилители, активные фильтры и усилители мощности.
Рассмотрим простейший резонансный усилитель: Здесь Свх и Свых – обычные разделительные конденсаторы, R1 и R2 – резисторы базовой цепи, Rэ и Сэ – элементы обратной связи по постоянному току (для термостабилизации) и Lконт и Сконт – элементы резонансного контура. Это обычный каскад с ОЭ, но вместо коллекторного сопротивления стоит резонансный контур, резонансная частота которого рассчитывается по формуле:
а сопротивление на этой частоте равно бесконечности, практически определяется потерями контура. При отступлении от резонансной частоты сопротивление контура резко падает, и, следовательно, падает коэффициент усиления транзистора, см. рис.:
А Df определяется формулой:
где Qэкв – добротность контура для эквивалентной схемы. Конечно, колебательный контур и сам по себе может осуществлять электрические колебания с частотой fp, но не бесконечно долго. Только транзистор способен усиливать эти колебания. При этом коэффициент усиления может быть большим (достигать 1000), шум в таком каскаде минимален, так как полоса частот очень узкая, температурный дрейф исключён. ОУ в резонансных усилителях не используются. В микроэлектронике делают специальные усилители, к которым можно подключить внешние L и C, или только L. Такие усилители, а также просто транзисторные каскады используются на частотах свыше 10 кГц, так как для более низких частот требуются большие конденсаторы и индуктивности, и это не удобно.
Время восстановления схемы
где RвыхЭП – выходное сопротивление эмиттерного повторителя (закрытого или почти закрытого). Для повышения коэффициента передачи эмиттерного повторителя и улучшения линейности выходного напряжения резистор RЭ должен иметь большое сопротивление, т.е. время восстановления схемы резко увеличивается, а ее быстродействие снижается. Для устранения этого недостатка в цепь эмиттера вводят дополнительный источник напряжения – ЕЭ. В этом случае ток заряда конденсатора увеличивается:
и процесс восстановления довольно быстро заканчивается (см. рис.4г). Ориентировочно можно считать, что время восстановления
ЛЕКЦИЯ 11. ТРИГГЕРЫ 1. Устройство триггера 2. Насыщенный и ненасыщенный триггеры 3. Условия работоспособности триггера 4. Триггер Шмитта на биполярных транзисторах 5. Триггер Шмитта на операционном усилителе 6. Компараторы Устройство триггера Триггером называют устройство, имеющее два устойчивых состояния равновесия и способное скачком переходить из одного состояния в другое под воздействием внешнего управляющего сигнала. Триггеры могут быть построены как на дискретных элементах, так и на интегральных микросхемах. Схема триггера на биполярных транзисторах n-p-n типа приведена на рис.1. Триггер представляет собой два усилителя на транзисторах VT1 и VT2. Выход каждого усилителя соединен с входом другого. Обратная связь, получаемая в результате такого соединения усилителей, является положительной. Оба транзистора в триггере работают в ключевом режиме, поэтому триггер можно рассматривать и как схему, в которой последовательно включены два транзисторных ключа, причем выходное напряжение первого непосредственно управляет вторым, а выходное напряжение второго ключа – первым. Обычно используют симметричную схему, т.е.
Триггер Шмитта Имеет два пороговых уровня срабатывания для перехода из одного устойчивого состояния в другое. Передаточная характеристика имеет гистерезисный характер (см. рис.1). При Uвх < Uпор1 триггер Шмитта находится в одном из устойчивых состояний, например, когда Uвых = Е0. Как только входное напряжение достигает порогового уровня срабатывания U пор1, схема скачком переходит в другое устойчивое состояние (рабочий режим), когда Uвых = Е1. Дальнейшее повышение входного напряжения не приводит к изменению состояния схемы. Однако уменьшение Uвх до порогового уровня отпускания Uпор2 вызывает скачкообразное возвращение схемы в исходное состояние (Uвых = Е0). Пороговые уровни срабатывания и отпускания, а следовательно, ширина петли гистерезиса определяются элементами схемы.
Компараторы Компаратор - это устройство сравнения, которое вырабатывает выходной сигнал в момент равенства двух напряжений, подаваемых на входы. Схема компаратора на операционном усилителе показана на рис.1а. Диаграмма выходного напряжения показана на рис.1б. В этой схеме опорный сигнал подается на не инвертирующий вход. Петля отрицательной обратной связи здесь не используется. В связи с этим коэффициент усиления ОУ очень большой. Когда сигнал на инвертирующем входе U- = Eоп, то выходное напряжение равно нулю. Незначительное отклонение входного напряжения U- в сторону уменьшения (U- < Eоп) приводит к резкому росту выходного напряжения Uвых до значения Точность сравнения сигналов составляет величину
Величина D определяет зону неопределенности компаратора. Рассмотренная схема имеет ограниченный диапазон входных напряжений. Если необходимо сравнивать большие величины входных напряжений можно использовать схему не инвертирующего компаратора, приведенную на рис.2. Компаратор срабатывает, когда напряжение на не инвертирующем входе U+ проходит через нуль. Чтобы U+ было равно нулю, сигналы U1 и U2 должны иметь противоположные знаки. Так как то условие срабатывания U+ = 0 имеет вид Эту схему можно функционально расширить, если к прямому входу ОУ подключить еще несколько резисторов. При этом компаратор будет срабатывать, когда приведенная к прямому входу алгебраическая сумма входных напряжений будет больше или меньше нуля. Если к прямому входу включить диоды (пунктир), то напряжение на прямом входе компаратора не может превысить значения Для стандартных частотно скорректированных ОУ скорость нарастания выходного напряжения Vнар» 1 В/мкс. Таким образом, переход, например с –12 В до +12 В составляет 24 мкс. Для ОУ без частотной коррекции скорость нарастания увеличивается, соответственно уменьшается время срабатывания схемы. На основе быстродействующих ОУ могут быть построены компараторы с малым временем переключения. / 8.1(1), 8.1(6), 8.2(4) / Контрольные вопросы 1. Что называют триггером? 2. Насыщенные и ненасыщенные триггеры. 3. Условие насыщения. 4. Триггеры с раздельным запуском. 5. Триггер Шмитта. 6. Что такое компараторы?
ЛЕКЦИЯ 12. ДЕТЕКТИРОВАНИЕ 1. Нелинейные или параметрические цепи. 2. Детектирование АМ – колебаний. 3. Линейный детектор 4. Коэффициент передачи детектора. 5. Квадратичный детектор.
Линейный детектор. Рассмотрим работу детектора при сильном сигнале. В этом случае ВАХ диода аппроксимируется кусочно-линейной зависимостью:
где S – крутизна ВАХ диода. Проанализируем сначала работу детектора в том случае, когда на его вход подается немодулированный сигнал
Ток диода, протекая по RC -цепи, будет заряжать емкость С до некоторого напряжения В те моменты времени, когда результирующее напряжение uд положительно (т.е. на диоде прямое смещение), через диод будет протекать ток. Емкость С будет заряжаться с постоянной времени
В установившемся режиме напряжение на емкости колеблется относительного некоторого среднего напряжения Изменения напряжений За время разряда напряжение на емкости изменяется незначительно, поэтому можно считать, что Таким образом, напряжение на диоде равно:
Процессы, происходящие в детекторе, иллюстрируются графиками рис.5. Диод работает с отсечкой тока, т.е. ток течет через диод лишь в течение небольшой части периода, которая определяется углом отсечки q. При этом ток имеет вид последовательности импульсов, представляющей собой усеченную синусоиду. Можно показать, что угол отсечки не зависит от амплитуды входного сигнала, а является величиной постоянной и определяется исключительно параметрами схемы S и R. Угол отсечки можно определить из выражения (6) как значение
Для косинусоидальных импульсов тока постоянная составляющая
Подставляя это выражение в (7), получаем уравнение, определяющее угол отсечки q:
Таким образом, угол отсечки зависит только от параметров схемы. Из (7) получаем выражение для составляющей тока
Так как угол отсечки q является величиной постоянной, составляющая тока
Квадратичный детектор. Для малых амплитуд входного сигнала характеристику диода можно аппроксимировать полиномом второй степени
Полагаем сопротивление R малым. Тогда uд»
Постоянная составляющая тока, равная
Эта зависимость является характеристикой детектирования. Она имеет квадратичный характер, и потому диодный детектор колебаний малой амплитуды называется квадратичным детектором. При квадратичном детектировании могут возникнуть большие нелинейные искажения. Амплитудно-модулированное колебание можно рассматривать как почти гармоническое
Из-за нелинейности характеристики детектирования изменение амплитуды входного сигнала вызывает непропорциональное изменение постоянной составляющей тока детектора, поэтому низкочастотные колебания на выходе детектора искажаются по сравнению с огибающей АМ -колебания. Подставляя (14) в (13), получаем
В спектре тока, а значит, и выходного напряжения детектора имеются две низкочастотные составляющие: частоты W передаваемого сигнала с амплитудой
величина которого пропорциональна коэффициенту модуляции.
Наличие сильных искажений (при m =100% Кг = 25%) является недостатком квадратичного детектора, поэтому он не используется в тех случаях, когда требуется неискаженно воспроизведение передаваемой информации, например, в радиовещании, телевидении. Однако квадратичное детектирование часто применяется, когда требуется получить выходное напряжение, пропорциональное мощности входного сигнала (например, в измерительной технике). Оно используется также при детектирования радиоимпульсов с прямоугольной огибающей; в этом случае искажения не возникают, т.к. ток Как отмечалось, диодные детекторы обычно бывают квадратичными при амплитудах входных сигналов U £ 0.1¼0.2 В и линейными при U ³ 0.5¼1 В. Чтобы избежать искажений, следует принимаемый АМ -сигнал усилить до детектирования настолько, чтобы его амплитуда была достаточно большой. Амплитудный детектор может быть также построен на транзисторах или на лампах. В транзисторных детекторах детектирование происходит за счет нелинейности коллекторно-базовой характеристики. В ламповых детекторах – за счет нелинейности входной (сеточной) характеристики или анодно-сеточной характеристики.
Следует отметить, что детектирование АМ -сигнала невозможно без несущей частоты, т.к. при воздействии на нелинейный элемент колебаний без несущей комбинационное колебание частоты W не возникает. Для детектирования колебаний без несущей (балансная АМ, АМ с одной боковой частотой) необходимо восстановить несущее колебание в приемном устройстве. Это осуществляется при помощи местного генератора, который управляется (синхронизируется) пилотсигналом. / 8.1(1), 8.1(3), 8.2(1)8.2(4) /
Контрольные вопросы 1. Детектирование. 2. Два элемента в обобщенной схеме детектора. 3. В качестве какого элемента в детекторах используется полупроводниковый диод? 4. Что называется коэффициентом передачи детектора? 5. Что называется квадратичным детектором?
Фазовая модуляция Два вида угловой модуляции: фазовая и частотная. Фазовая модуляция (ФМ) заключается в изменении фазы j переносчика
где а - коэффициент пропорциональности. Амплитуда колебания при ФМ не изменяется, поэтому аналитическое выражение ФМ колебания имеет вид
Если модуляция осуществляется гармоническим сигналом
Первые два слагаемых в выражении (3) определяют фазу немодулированного колебания, третье - изменение фазы колебания в результате модуляции. ФМ -колебание характеризуется векторной диаграммой рис.1, построенной на плоскости, вращающейся по часовой стрелке с угловой частотой wо. Немодулированному колебанию соответствует неподвижный вектор Uo. Фазовая модуляция заключается в периодическом с частотой W повороте вектора U относительно Uo на угол Крайние положения вектора U обозначены U' и U ". Максимальное отклонение фазы модулированного колебания от фазы немодулированного колебания
называется индексом модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала. Выражение для ФМ колебания можно переписать в виде
Мгновенная частота ФМ колебания
Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания wо на величину Наибольшее отклонение частоты w от несущей частоты wо называется девиацией частоты Dwд = М W
Частотная модуляция Частотная модуляция заключается в изменении мгновенной частоты переносчика пропорционально первичному сигналу:
Мгновенная фаза ЧМ колебания равна
Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде
В простейшем случае модуляции гармоническим колебанием Аналитическое выражение для ЧМ сигнала
Индекс модуляции М =Dwд/W. Тогда ЧМ колебание можно записать в виде
Из сказанного следует, что ФМ и ЧМ колебания имеют много общего. Так, колебание вида (10) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты Dwд). Наряду с отмеченным сходством ЧМ и ФМ между ними имеется и существенно отличие, связанное с различным характером зависимости величин М и DwД от частоты W первичного сигнала: - при ФМ индекс модуляции не зависит от частоты W, а девиация частоты пропорциональна W; - при ЧМ девиация частоты не зависит от частоты W, а индекс модуляции обратно пропорционален W. В общем случае любое колебаний с угловой модуляцией может быть получено как в результате ФМ первичным сигналом x(t), так и ЧМ первичным сигналом x1 (t)= Средняя мощность ЧМ (ФМ) колебания. Так как обычно W << w, то можно считать рассматриваемые колебания в пределах периода T =2p/w гармоническими. Средняя мощность такого колебания за период T
Такой же она будет и в другие периоды, а поэтому и за период низкой частоты. Следовательно, средняя мощность при ЧМ и ФМ остается такой же, как и в отсутствие модуляции; происходит лишь ее перераспределение между составляющими спектра.
Спектр ФМ и ЧМ колебаний При узкополосной модуляции M < 1, спектр ЧМ (ФМ) колебаний аналогичен спектру простейшего АМ колебания. Он содержит компоненты несущей частоты wо и двух боковых частот wо+W и wо-W:
Параметром, определяющим амплитуды боковых частот, здесь является индекс модуляции M. Ширина спектра узкополосной угловой модуляции такая же, как и при АМ: она равна удвоенной частоте модуляции. Несмотря на идентичность спектров, рассматриваемое колебание отличается от АМ колебания, что является следствием различия в знаках (т.е. сдвиге фаз на 180о) компонент нижней боковой частоты. Это иллюстрирует векторная диаграмма рис.3. При широкополосной угловой модуляции M >> 1. В этом случае выражение для спектра имеет достаточно сложный вид. На рис.5 в качестве примера приведен спектр ФМ (ЧМ) сигнала при модуляции гармоническим сигналом. Практическая ширина спектра близка к удвоенной девиации частоты DwЧМ,ФМ» 2Dwд = 2 M W. (13) При модуляции гармоническим сигналом спектр ЧМ и ФМ колебаний оказывается дискретным, симметричным относительно wо и содержащим бесконечное число боковых частот вида wо± n W с амплитудами An = UoJn(M) (Jn(M) -функции Бесселя n -го порядка). В качестве примера на рис.4 приведен спектр для M =4. Соотношения между функциями Бесселя различных порядков, а следовательно, и между амплитудами различных боковых компонент определяются индексом модуляции M. При некоторых значениях M отдельные компоненты могут исчезнуть (Jn(M) =0). Это же относится к амплитуде несущей частоты, которая обращается в ноль при M =2.4; 5.6¼ Наличие бесконечно большого числа боковых компонент спектра означает, что теоретически спектр ФМ и ЧМ колебания является бесконечно широким. Однако функции Бесселя, начиная с некоторых n < M, быстро убывают с ростом n. Это позволяет ограничить полезный (практический) спектр таких сигналов определенным количеством боковых частот. При ограничении спектра необходимо учитывать влияние двух противоречивых факторов: в более узкой полосе частот ослабляется влияние помех, но одновременно увеличиваются искажения сигнала из-за отсутствия опускаемых составляющих. На практике выбирают компромиссное решение. Если ограничиться в спектре боковыми составляющими, амплитуда которых не превосходит q % от максимальной амплитуды спектральной компоненты Ux, то для каждого M можно рассчитать соответствующую ширину спектра. Она окажется несколько большей 2 М W = 2Dwд. Из рис.4 следует, что для M =4 при q =20% ширина спектра DwЧМ,ФМ= 2(M +3)W = 2(Dwд+3W). При больших индексах модуляции (порядка десятков и сотен), практическая ширина спектра, подсчитанная подобным образом, близка к удвоенной девиации частоты. При изменении амплитуды Х модулирующего сигнала спектры ФМ и ЧМ колебаний изменяются одинаково. При возрастании Х прои
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.105.46 (0.013 с.) |



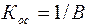






















 , мы можем смоделировать эти действия: нам нужен один дифференцирующий усилитель, один
, мы можем смоделировать эти действия: нам нужен один дифференцирующий усилитель, один




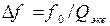
 , (25)
, (25)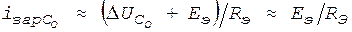
 . (26)
. (26) ,
,  ,
, 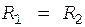 . В принципе, в приведенной схеме возможно состояние электрического равновесия, при котором оба транзистора VT1 и VT2 открыты и находятся в активной области. В этом случае токи
. В принципе, в приведенной схеме возможно состояние электрического равновесия, при котором оба транзистора VT1 и VT2 открыты и находятся в активной области. В этом случае токи  и
и  и падения напряжений на элементах схемы равны между собой. Однако такое состояние является неустойчивым и любые флуктуации тока или напряжения (или разброс параметров элементов схемы) приведут к лавинообразному процессу нарастания тока одного и убывания тока другого транзисторов. Например, увеличение коллекторного тока
и падения напряжений на элементах схемы равны между собой. Однако такое состояние является неустойчивым и любые флуктуации тока или напряжения (или разброс параметров элементов схемы) приведут к лавинообразному процессу нарастания тока одного и убывания тока другого транзисторов. Например, увеличение коллекторного тока  . Это, в свою очередь, приведет к уменьшению напряжения
. Это, в свою очередь, приведет к уменьшению напряжения  и тока
и тока  транзистора VT2. Последнее вызовет уменьшение тока
транзистора VT2. Последнее вызовет уменьшение тока  ,
,  . Следовательно, произойдет дальнейшее увеличение тока
. Следовательно, произойдет дальнейшее увеличение тока  , которое определяется свойствами выходного каскада и близко к + ЕО. Если U- > Eоп, то Uвых =
, которое определяется свойствами выходного каскада и близко к + ЕО. Если U- > Eоп, то Uвых =  .
. .
. ,
, .
. 0.7 В.
0.7 В. при
при  ; (3)
; (3) при
при  ,
,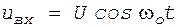 . (4)
. (4) . Это напряжение оказывается приложенным к диоду в обратном направлении. Результирующее напряжение на диоде будет равно
. Это напряжение оказывается приложенным к диоду в обратном направлении. Результирующее напряжение на диоде будет равно 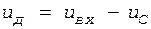 . (5)
. (5) , где
, где 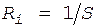 - внутреннее сопротивление диода. При отрицательном uд диод запирается, и емкость С разряжается через сопротивление R с постоянной времени
- внутреннее сопротивление диода. При отрицательном uд диод запирается, и емкость С разряжается через сопротивление R с постоянной времени 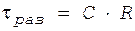 . Причем
. Причем  , т.к. в реальных схемах всегда выполняется условие
, т.к. в реальных схемах всегда выполняется условие .
. =
=  , где
, где  - постоянная составляющая тока диода.
- постоянная составляющая тока диода. и
и 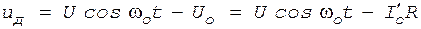 . (6)
. (6)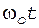 , при котором напряжение на диоде uд равно нулю (или из рис.5):
, при котором напряжение на диоде uд равно нулю (или из рис.5): . (7)
. (7)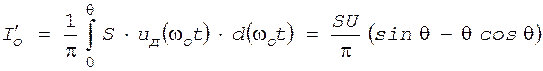 . (8)
. (8)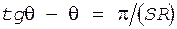 . (9)
. (9) . (10)
. (10) . (12)
. (12) .
. , под действием входного сигнала получит приращение
, под действием входного сигнала получит приращение . (13)
. (13) с медленно меняющейся амплитудой
с медленно меняющейся амплитудой . (14)
. (14) . (15)
. (15) и ее второй гармоники с амплитудой
и ее второй гармоники с амплитудой  . Искажения при квадратичном детектировании можно характеризовать коэффициентом гармоник, величина которого пропорциональна m:
. Искажения при квадратичном детектировании можно характеризовать коэффициентом гармоник, величина которого пропорциональна m: , (16)
, (16) также имеет прямоугольную форму.
также имеет прямоугольную форму. пропорционально первичному сигналу x(t):
пропорционально первичному сигналу x(t): , (1)
, (1)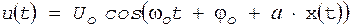 . (2)
. (2)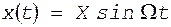 , то мгновенная фаза
, то мгновенная фаза . (3)
. (3) .
.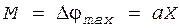 (4)
(4) . (5)
. (5) . (6)
. (6) , что позволяет рассматривать ФМ колебание как модулированное по частоте.
, что позволяет рассматривать ФМ колебание как модулированное по частоте. . (7)
. (7)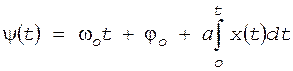 . (8)
. (8) . (9)
. (9) мгновенная частота колебания равна
мгновенная частота колебания равна  , где
, где  - девиация частоты, т.е. максимальное отклонение частоты от несущей wО, вызванное модуляцией.
- девиация частоты, т.е. максимальное отклонение частоты от несущей wО, вызванное модуляцией. . (10)
. (10)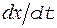 (т.к. фаза колебания представляет собой интеграл от частоты). Следует также отметить, что частотная и фазовая модуляции различаются также способами их осуществления.
(т.к. фаза колебания представляет собой интеграл от частоты). Следует также отметить, что частотная и фазовая модуляции различаются также способами их осуществления. . (12)
. (12)



