
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения математической логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Формальные теории Логика высказывания является одной из разновидностей формальных теорий. Формальная теория 1) множество символов 2) множество слов 3) подмножество 4) множество отношений Множества
Формулы в числителе называются посылками, а формула в знаменателе – заключением, или секвенцией. Иногда обозначение правила вывода справа от черты дроби опускают, если ясно, о чем идет речь. Вывод формулы Если формула Если некоторый набор гипотез позволяет вывести формулу, то добавление гипотез не должно приводить к невыводимости:
Интерпретацией формальной теории Формула называется общезначимой (или тавтологией), если она истинна в любой интерпретации. Исчисление высказываний Рассмотрим исчисление высказываний как формальную теорию. В алгебре высказываний имеется понятие истинности. В соответствии с общей конструкцией формальных теорий в алгебре высказываний вводятся следующие понятия: 1. Множество символов – – (, ) – служебные символы; – 2. Формулы: – переменные суть формулы; – если 3. Аксиомы:
Здесь приведены схемы аксиом. Поскольку 4. Правило: Другие связки вводятся определениями (а не аксиомами):
Если в формулу При конструктивном определении исчисления высказываний помимо приведенного правила modus ponens вводится еще одно, называемое правилом подстановки: если формула Теорема 1. Доказательство. В аксиому Тем самым выведем формулу По второй аксиоме
Теперь видим, что по правилу modus ponens выводится формула Подключаем По правилу modus ponens Теорема 2. Доказательство. По правилу modus ponens Теорема 3. Если Доказательство. Дано: существуют Доказательство проводим по индукции. Необходимо доказать, что если существует вывод 1. Докажем, что а) б) в) 2. Пусть
Получаем При Обратная теорема: Доказательство. Примем выведенное утверждение Следствие 1. Если Следствие 2. Доказательство. Следствие 3. Другие теоремы:
Способы доказательства теорем в исчислении высказываний следующие: 1. Использовать методику, приведенную выше. Ее суть – применение аксиом, правил вывода и поиск унификаторов. Каждая выведенная теорема подключается к списку
2. С помощью теоремы дедукции привести выводимую в ИВ (исчислении высказываний) формулу к виду теоремы (т.е. от предложенного для вывода
Далее записать формулу АВ (алгебры высказываний):
Можно также использовать рассмотренные в АВ эквивалентности либо составить таблицу истинности (с помощью ЭВМ) и убедиться в тавтологичности этой формулы (т.е. в том, что при любых значениях пропозициональных переменных она принимает значение «истина»). Если это не так, то формула ИВ не является выводимой. 3. В большинстве случаев проще доказывать невыводимость противоположной формулы. Это так называемый метод доказательства от противного:
Теперь запишем соответствующую формулу АВ (в булевой форме) и преобразуем, используя эквивалентности АВ:
Это значит, что соответствующая формула ИВ выводима: 4. Доказательство от противного лежит в основе метода резолюции, который базируется на выводимости теоремы
Эту теорему нужно доказать. Используем алгебру высказываний (АВ), считая символ «+» дизъюнкцией, а символ «•» конъюнкцией:
Придадим
Итак, при любых значениях Полученное правило называется правилом резолюции. Пользуясь дедукцией (точнее, обратной теоремой дедукции), это правило можно записать в виде
Этим правилом вывода, доказанным вполне строго, можно пользоваться наряду с правилом МР. Знаменатель правила Исчисление предикатов Пусть Предположим, таких функций несколько: Примеры: 1. Пусть 2. Задано произвольное множество Частные случаи: – – ( Если функции сигнатуры являются произвольными отношениями, то пара ( Пусть дана алгебра ( Пример. (2; 4; 10; «+»); 2 + 2 = 4; 2 + 4 = 6 (2; 4; 6; 10; «+») – все то, что можно получить, и является замыканием (все четные числа). Элементы сигнатуры называются функторами; С введением предикатов алгебра логики приобретает динамику. Аргументы (термы), вообще говоря, пробегают множество значений в некоторой области. Некоторые утверждения высказываются для случаев, когда некоторая переменная (терм) пробегает все множество значений и когда она принимает некоторые значения из допустимых. Указанием на пункт А или Б являются кванторы: «все» – All: С помощью кванторов исчисление высказываний обогащается новым типом формул: Переменные, по отношению к которым применим квантор, называются связанными, остальные свободными. В дополнение к этому в исчислении предикатов добавляются новые аксиомы типа П1 MP: Формулой исчисления предикатов является любой стандартный набор, содержащий обычные пропозициональные переменные, снабженные кванторами Одной из основных задач является приведение формул исчисления предикатов к виду, удобному для вывода. Основные идеи такого приведения: 1. Пример. Доказать, что число 36 делится на 6. Вместо этого докажем две другие теоремы: 36/2 и 36/3. После доказательства этих теорем следует, что (36/2) и (36/3) 2. Избавиться от отрицаний перед кванторами:
3. Пример. Пусть дана плоскость и вектор нормали. Высказывание 1: все прямые, лежащие в плоскости, перпендикулярны вектору нормали. Высказывание 2: прямая, лежащая в плоскости, перпендикулярна к вектору нормали (квантор
Алгоритм заключается в выполнении следующих шагов: Шаг 1. Избавление от импликаций:
Шаг 2. «Протаскивание» отрицаний:
Шаг 3. Вспомогательная операция – разделение связанных переменных. Основная идея заключается в том, что каждая связанная переменная может встречаться только два раза: первый раз – в обозначении квантора, второй – в обозначении терма:
Например, Шаг 4. Приведение к предваренной форме. Основная ид
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.028 с.) |

 :
: ,образующих алфавит;
,образующих алфавит;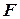 в алфавите, которые называются формулами;
в алфавите, которые называются формулами;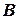

 (не обязательно бинарных) на множестве формул, которые называются правилами вывода.
(не обязательно бинарных) на множестве формул, которые называются правилами вывода. – формулы теории
– формулы теории 
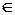
 непосредственно выводима (или доказуема) из формул
непосредственно выводима (или доказуема) из формул  по правилу вывода
по правилу вывода  .
. , что
, что  , а любая из формул
, а любая из формул  является либо аксиомой, либо исходной формулой
является либо аксиомой, либо исходной формулой  , либо непосредственно выводимой из ранее полученных формул.
, либо непосредственно выводимой из ранее полученных формул.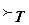

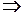

 называется функция I:
называется функция I: 
 и
и  – пропозициональные переменные.
– пропозициональные переменные.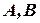 – формулы, то (
– формулы, то ( ;
;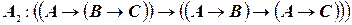 ;
; .
. – любые формулы, то аксиом бесконечно много. (В конструктивном определении исчисления высказываний в указанные аксиомы входят конкретные формулы, но вводится еще одно правило вывода.)
– любые формулы, то аксиом бесконечно много. (В конструктивном определении исчисления высказываний в указанные аксиомы входят конкретные формулы, но вводится еще одно правило вывода.) – modus ponens.
– modus ponens. .
. подставить соответственно формулы
подставить соответственно формулы  , то получится формула, которая называется частным случаем исходной. Набор подстановок
, то получится формула, которая называется частным случаем исходной. Набор подстановок  называется унификатором. Формула
называется унификатором. Формула 
 :
:  вместо
вместо  .
. :
:  . Подставим
. Подставим  .
.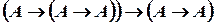 .
. .
. , что и требовалось доказать.
, что и требовалось доказать. – гипотеза
– гипотеза 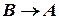 , что и требовалось доказать.
, что и требовалось доказать. , такие, что
, такие, что 

 – либо аксиомы, либо
– либо аксиомы, либо 
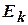 ,
, 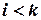 .
. ,
,  ,…
,… . По правилу МР
. По правилу МР  , или
, или 
 в виде гипотезы и используя
в виде гипотезы и используя  , по правилу МР получаем
, по правилу МР получаем 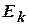 :
: 

 .
. .
.  – это гипотеза индукции, которая считается выведенной. По МР
– это гипотеза индукции, которая считается выведенной. По МР  . Опять-таки,
. Опять-таки,  – гипотеза вывода, и по МР
– гипотеза вывода, и по МР  . Результат:
. Результат:  .
. приходим к утверждению теоремы.
приходим к утверждению теоремы. .
. в качестве гипотезы. Если
в качестве гипотезы. Если 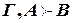 , что и требовалось доказать.
, что и требовалось доказать. , то
, то  (правило транзитивности).
(правило транзитивности).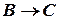 – гипотезы. Значит,
– гипотезы. Значит,  . По теореме дедукции
. По теореме дедукции  ,
, 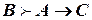 (правило сечения).
(правило сечения). ;
;  ;
; 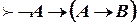 ;
; ;
;  ;
; ;
;  , ….
, ….
 , где
, где 
 .
.

 .
.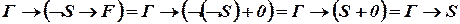 .
. .
. , что соответствует аналогичной формуле АВ, которую запишем в булевой форме:
, что соответствует аналогичной формуле АВ, которую запишем в булевой форме:

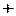
 .
. поочередно значения 0 и 1:
поочередно значения 0 и 1:



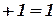 ;
; , либо в виде правила вывода
, либо в виде правила вывода  .
. :
: 
 -парной (или
-парной (или 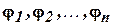 . Этот набор называется сигнатурой, что обозначается как
. Этот набор называется сигнатурой, что обозначается как 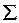 . Пара (
. Пара (
 .
. . Применение операции
. Применение операции  – терм. Отображение некоторого множества термов во множество {И, Л} называется атомом. Он состоит из двух объектов:
– терм. Отображение некоторого множества термов во множество {И, Л} называется атомом. Он состоит из двух объектов: 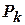
 , где
, где  ; «существует» – Exists:
; «существует» – Exists:  .
.
 ;
;  .
.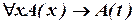 ; П2
; П2  ;
;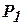 :
:  ;
;  :
:  .
. и
и  . Кванторы в этой теории применяются лишь к термам. Такая теория называется теорией первого порядка. В теориях высших порядков кванторы применяются также к литералам – именам пропозициональных переменных и предикатов.
. Кванторы в этой теории применяются лишь к термам. Такая теория называется теорией первого порядка. В теориях высших порядков кванторы применяются также к литералам – именам пропозициональных переменных и предикатов.

 ,
, 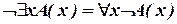 .
.




 .
. .
. .
.

 – не имеет смысла;
– не имеет смысла;  – правильно.
– правильно.


