Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквивалентность автоматов. МинимизацияСодержание книги Поиск на нашем сайте
Рассмотрим два автомата:
Состояния Автоматы Рассмотрим изменения состояний и выходов автомата с изменением времени. На каждом такте подается входной сигнал (символ), преобразуется внутреннее состояние, возникает сигнал выхода. Рассмотрим следующий такт. Действия аналогичны:
Итак, автомат преобразует слова (как и машина Тьюринга, частным случаем которой является конечный автомат). Рассмотрим состояние
а б Рис. 4.4. Достижимое состояние (а) и класс достижимых состояний (б)
Рассмотрим два автомата Иными словами, автоматы называются эквивалентными, если для каждого состояния Пример:
На начальном этапе отыскиваем классы
Приходим к автомату, внутренние состояния которого отождествляются с найденными классами эквивалентных состояний:
У полученного и исходного автоматов внешнее поведение одинаково.
Контрольное задание
Воспользовавшись данными, приведенными в табл. 4.2, выполнить следующее: а) построить граф для каждого из заданных автоматов (рекомендуется использовать VISIO); б) минимизировать автоматы, построить графы, проверить правильность минимизаций на словах длиной 20; в) установить, эквивалентны ли заданные автоматы, проверить на слове длиной 20.
Таблица 4.2 Варианты задания
Окончание табл. 4.2
Автоматы Мили и Мура. Размеченные графы Рассмотренные ранее автоматы – это классические автоматы Мили. Автомат Мура – это автомат, выходы которого зависят только от текущего состояния:
где Автомат Мура – частный случай автомата Мили. Оказывается, для каждого автомата Мили существует эквивалентный ему автомат Мура. Для доказательства каждое из состояний расщепляется на несколько состояний, для каждого из которых выход зависит только от состояния, но не от входа. При табличном задании автомата Мура вместо двух таблиц рассматривается одна, которая называется размеченной функцией перехода:
Несколько изменяется представление графа. Обозначение выхода ставится возле каждого узла (рис. 4.5).
Рис. 4.5. Графическое представление автомата Мура
Автоматные языки Общая теория конечных автоматов сводится к анализу и синтезу автоматов. Анализ: по Частные случаи практически важных КА (конечных автоматов): – сумматор; – задержка – счетчик. Автоматы подразделяются на преобразователи и распознаватели. Иногда вместо распознавателя употребляется термин «акцептор». Все предыдущие автоматы являлись преобразователями. В настоящее время одно из основных применений автомата – установление факта принадлежности подстроки данной строке. Рассмотрим задачу: установить наличие в заданной строке слова «резец». Синтез соответствующего автомата начинается с построения графа (рис. 4.6).
Рис. 4.6. Граф распознавания заданного слова
По графу строим таблицу, описывающую работу автомата-распознавателя:
Далее подаем некоторую строку. Подстрока считается выявленной, если на выходе появляется единица:
Полученные таблицы для реализации функции В качестве задания осуществить проверку наличия какого-нибудь слова (или предложения) в произвольно выбранном тексте. Например, рассмотреть исходный текст некоторой программы на алгоритмическом языке PASCAL и проверить наличие выражения «for I:=» в этом тексте. Основной технический аппарат при изучении автоматных языков – акцепторы, автоматы-распознаватели. Распознаватели осуществляют выделение всех входных предложений, принадлежащих языку. Автоматные языки – очень узкий класс всех возможных языков. Словарь – это конечное множество. Элементы словаря – символы (буквы). Предложение – все конечные последовательности символов из заданного словаря.
Множество Грамматика – конечный механизм задания языка. Существует два вида грамматик – порождающая и распознающая: первая – это механизм, позволяющий строить все допустимые предложения, вторая – отсеивает из множества Синтаксис – правила построения языка. Возможности автоматов Конечные автоматы позволяют избежать использования в программах, реализующих алгоритмы, условного оператора «if», а также операторов выбора (например, «case»). Поэтому «автоматный» стиль программирования предпочтителен при построении сложных программ. Рассмотрим несколько примеров, демонстрирующих преимущества использования автоматов в процессе решения некоторых задач. Счетчик. Требуется создать устройство, которое на каждом такте выдает целое число, большее предыдущего на единицу; при достижении некоторого предельного значения серия выводимых значений повторяется. Пусть предельное значение равно шести. Автомат, реализующий алгоритм, является автоматом Мура и может быть описан в стандартном виде:
Предположим, что вслед за этим счетчиком предполагается разместить еще один, который бы отсчитывал количество шестерок. В таком случае достаточно в качестве выходного алфавита принять следующий набор:
Однако следует отметить, что счетчики рассмотренного типа не позволяют считать до бесконечности. Это ограничение принципиально для конечных автоматов. Однако данной схемы достаточно для реализации обычных электронных часов [1]. Счетчик является примером так называемых автономных автоматов, входной алфавит которых содержит единственный символ. Если считать, что в каждой вершине графа имеется один выход, причем выходной сигнал совпадает с номером состояния, то он является эквивалентом отношения порядка, а граф автономного автомата – это простой ориентированный граф [2, 3]. Для входного слова достаточной длины выходное слово автономного автомата содержит периодически повторяющееся подслово. Проверка четности. Пусть входной алфавит содержит два символа – ноль и единицу. Требуется построить алгоритм, согласно которому на выходе повторяется входное слово, но после каждого подслова, содержащего три символа, должен быть вставлен символ «0», если количество единиц в подслове четно, и символ «1» в противном случае. Прежде всего отметим, что выходной алфавит конструируемого автомата не может состоять только из нуля и единицы, так как количество символов во входном и выходном словах должно быть одно и то же (требование автоматности). Это требование удовлетворяется введением такого выходного алфавита:
Выполним кодирование состояний и выходов, сопоставляя состояние «-» и номер 0, «0» – номер 1, «1» – 2, «00» – 3, «01» – 4, «10» – 5, «11» – 6; выход «0» и номер элемента алфавита 0, выход «1» и номер 1, «00» – 2, «01» – 3, «10» – 4, «11» – 5. Тогда таблица построенного автомата примет такой вид:
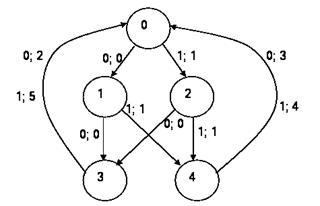
Граф этого автомата изображен на рис. 4.7. Отметим, что состояния 3 и 6 эквивалентны. Это же относится и к паре состояний 4 и 5. Поэтому в данном случае имеется возможность минимизировать найденный автомат, объединив состояния 3, 6 в класс 3 эквивалентных состояний, а классы 4, 5 – в класс 4. Минимизированный автомат, эквивалентный исходному, в таком случае можно изобразить графически (рис. 4.8) и в виде таблицы:
Если поставлена задача проверить четность в словах длиной n, то граф неминимизированного автомата будет содержать Таким образом, задача минимизации, т.е. построение автомата, эквивалентного исходному, но с меньшим количеством состояний, является очень важной.
Рис. 4.7. Граф автомата проверки четности
Рис. 4.8. Минимизированный автомат проверки четности
Сумматор. Пусть поставлена задача найти сумму двух чисел в троичной системе счисления. Сложение будем производить поразрядно с учетом возможного перенесения в старший разряд. Напрямую автомат построить в этом случае невозможно, поэтому требуется ввести в рассмотрение входной алфавит, состоящий из пар цифр. Учитывая, что слагаемые можно переставлять, кодировщик представим в виде матрицы X:
Например, пара цифр (1,2) кодируется как элемент X[1,2] = 3, как и пара цифр (2,1). Автомат суммирования может быть задан в виде матрицы
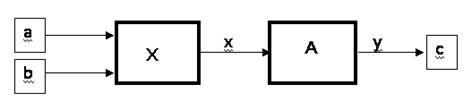
Собственно, сложение производится поразрядным (начиная с младшего разряда) пропусканием двух слов a и b (т.е. чисел, представленных в троичной системе счисления) через цепочку (рис. 4.9).
Рис. 4.9. Автоматное суммирование
Достоинством автоматного суммирования является то, что все действия ограничиваются нахождением элементов матриц X и А.
Автоматное декодирование. Рассмотрим основную идею на примере. Пусть задана таблица кодов, получаемых как пути в дереве (рис. 4.10). С движением от узла влево сопоставим символ «а», прямо – «б», вправо – «в». Таблица кодов имеет следующий вид:
В качестве номеров состояний автомата примем номера узлов, не являющихся листами; корень дерева имеет номер 0.
Рис. 4.10. Дерево кодирования
Выходной алфавит содержит буквы, соответствующие листам, а также пустой символ «-». В результате получаем таблицу автомата следующего вида:
Для проверки работоспособности построенного автомата предлагается самостоятельно получить выходное слово, если на вход подается слово «бабвабвббвбббвбббабв». Входное слово следует подавать в порядке слева направо (первый входной символ – б, второй – а, третий – б и т.д.). По каждой из рассмотренных задач желательно самостоятельно сконструировать автоматы, реализующие различные частные случаи. С помощью конечных автоматов решается огромное количество задач. Тем не менее, имеется множество задач, для которых не существует алгоритмического решения и, следовательно, нельзя построить автомат. Краткий перечень задач, для которых отсутствует алгоритм решения, таков [1]: 1. Проблема остановки. По описанию произвольного алгоритма и его исходных данных определить, остановится ли алгоритм на этих данных или будет работать вечно. 2. Проблема эквивалентности алгоритма. По двум произвольным алгоритмам определить, будут ли они выдавать одинаковые выходные результаты при одинаковых входных данных. 3. Проблема эквивалентности грамматики. По двум произвольным грамматикам установить, совпадают ли порожденные ими языки. 4. Проблема тотальности. По произвольному заданному алгоритму определить, будет ли он завершаться во всех возможных наборах.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 ,
, .
. из множества
из множества  автомата
автомата  и соответственно
и соответственно  из множества
из множества  автомата В называются неразличимыми, если
автомата В называются неразличимыми, если  .
.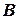 называются неразличимыми, если для любого состояния
называются неразличимыми, если для любого состояния  существует состояние
существует состояние  , такое, что
, такое, что  , и наоборот,
, и наоборот,  .
. ,
,  .
. автомата
автомата  называется достижимым из состояния
называется достижимым из состояния 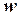 , что
, что  . Достижимые состояния образуют класс достижимых состояний (рис. 4.4).
. Достижимые состояния образуют класс достижимых состояний (рис. 4.4).

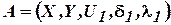 ,
,  и состояния
и состояния  . Автоматы называются эквивалентными, если
. Автоматы называются эквивалентными, если 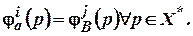
 существует эквивалентное ему состояние автомата
существует эквивалентное ему состояние автомата  . Эквивалентные автоматы обладают одинаковым внешним поведением, т.е. на одинаковые входные слова выдают одинаковые внешние слова. Автоматы могут различаться сложностью внутренней структуры, например, мощностью множеств
. Эквивалентные автоматы обладают одинаковым внешним поведением, т.е. на одинаковые входные слова выдают одинаковые внешние слова. Автоматы могут различаться сложностью внутренней структуры, например, мощностью множеств  и
и  . Среди всех эквивалентных автоматов имеется минимальный. Одной из основных задач является следующая: найти автомат, эквивалентный данному, но обладающий наименьшим количеством внутренних состояний. Такие задачи решаются последовательно путем выявления одного неразличимого состояния, двух неразличимых состояний,…,
. Среди всех эквивалентных автоматов имеется минимальный. Одной из основных задач является следующая: найти автомат, эквивалентный данному, но обладающий наименьшим количеством внутренних состояний. Такие задачи решаются последовательно путем выявления одного неразличимого состояния, двух неразличимых состояний,…,  неразличимых состояний, которые объединяются в классы
неразличимых состояний, которые объединяются в классы 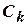 неразличимых состояний.
неразличимых состояний.

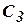

 ):
):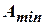
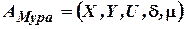 ,
,

 – алфавит входных сигналов;
– алфавит входных сигналов; 
 – алфавит выходных сигналов;
– алфавит выходных сигналов; 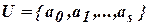 ,
,  ,
,  .
.
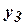


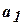
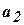
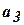



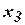

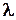 изучить особенности внешнего поведения автомата. Синтез: по внешнему поведению построить функции
изучить особенности внешнего поведения автомата. Синтез: по внешнему поведению построить функции  (автомат задержки – это автомат Мура);
(автомат задержки – это автомат Мура);



 – множество всех цепочек, построенных по данному словарю.
– множество всех цепочек, построенных по данному словарю. . Первая из цифр выводится на экран, вторая подается на выход, являющийся входом для следующего счетчика. Если на вход второго счетчика подается 0, то его состояние не меняется и на выход подается пустой символ. Если же подается единица, то он изменяет состояние так же, как и рассмотренный выше счетчик:
. Первая из цифр выводится на экран, вторая подается на выход, являющийся входом для следующего счетчика. Если на вход второго счетчика подается 0, то его состояние не меняется и на выход подается пустой символ. Если же подается единица, то он изменяет состояние так же, как и рассмотренный выше счетчик: . Выход после третьего символа состоит из двойки символов: «00», «01», «10», «11». Обозначим состояния автомата как «-», «0», «1», «00», «01», «10», «11», подразумевая под «-» стартовое состояние. После этого оказывается возможным построение автомата проверки четности в следующем виде:
. Выход после третьего символа состоит из двойки символов: «00», «01», «10», «11». Обозначим состояния автомата как «-», «0», «1», «00», «01», «10», «11», подразумевая под «-» стартовое состояние. После этого оказывается возможным построение автомата проверки четности в следующем виде: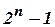 вершин, а минимизированного –
вершин, а минимизированного –  .
.