
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реализация метода Квайна – Мак-КласкиСодержание книги Поиск на нашем сайте
С помощью этого метода строят тупиковые НДФ (нормальные дизъюнктивные формы) и из множества тупиковых выбирают минимальные НДФ. Основой алгоритма являются следующие эквивалентности:
Первая часть алгоритма: 1. По заданной СНДФ строят эквивалентную НДФ, получаемую как дизъюнкцию всех нетривиальных попарных склеек. Если некоторый столбец булевых функций ни с чем не склеивается, то его переписывают заново. 2. После склеивания возможно появление элементарных одинаковых конъюнкций. Лишние нужно убрать. 3. Если дальнейшие склеивания неосуществимы, то переход к п. 4, иначе – к п. 1. В результате приходят к некоторой сокращенной нормальной дизъюнктивной форме. Вторая часть алгоритма (решение задачи о минимальном покрытии): 4. Рассматривают каждую элементарную конъюнкцию из полученной формулы и проверяют её вхождение в отдельные слагаемые исходной СНДФ. 5. Среди полученных элементарных конъюнкций могут оказаться и лишние. Их нужно отбросить. В результате получают тупиковые формы, реализующие минимальное покрытие. Их может оказаться несколько. Минимальная НДФ является одной из тупиковых. Замечания: – данный алгоритм неизбежно включает в себя прямой перебор; – алгоритм является NP-сложным (с ростом размерности сложность возрастает быстрее любой степени размерности); – дальнейшее упрощение можно осуществлять, отказавшись от требования нормальности. Пример. Требуется минимизировать булеву функцию, заданную в совершенной нормальной дизъюнктивной форме:
Сопоставим с этой функцией булеву матрицу
Рассмотрим первый и второй столбцы. Запишем их дизъюнкцию и вынесем общие множители:
Формально это действие сводится к тому, что переменная X2 подвергается удалению. Сопоставим с отсутствием этой переменной символ 2 (возможно использование и других символов):
Итак, первый и второй столбцы склеиваются. Первый и третий столбцы не склеиваются, так как в компонентах имеется более одного отличия. Далее по очереди выполняем склеивание столбцов, если это возможно (т.е. если в компонентах ровно одно отличие). Формальные действия для отдельных компонент отображаются следующими соотношениями: (0,1) (1, 2) Результаты склеивания заносим в качестве столбцов в новую матрицу. Некоторые столбцы не склеиваются с другими; записываем такие столбцы в новую матрицу без изменений. Чтобы учесть наличие несклеиваемых столбцов, те из них, которые участвуют в склейках, снабжаем дополнительным символом, например «+»:
F =
Выписываем преобразованную матрицу, отмечая номера склеиваемых столбцов, номера полученных столбцов и метки участия в дальнейших склейках:
Повторяем процесс склеивания:
Некоторые столбцы одинаковы: (1,3), (2,5), (6,7), (8,9), (11,12), (13,14). В каждой группе указанных столбцов оставляем по одному экземпляру и продолжаем склеивание:
После того, как в полученной таблице заменили три совпадающих столбца одним, приходим к окончательной сокращенной нормальной дизъюнктивной форме
Полученная таблица соответствует стандартной записи НДФ в следующем виде:
Таким образом, исходная функция приведена к дизъюнкции простых импликант
Выбрасывание последней импликанты не приводит к неэквивалентности, т.е. не появляются пустые столбцы. Поэтому минимальная дизъюнктивная нормальная форма (НДФ) для исходной функции имеет вид
Первая часть рассмотренного алгоритма программируется довольно просто. Нахождение минимального покрытия – нетривиальная задача. В некоторых случаях возможно существование нескольких тупиковых форм.
Контрольное задание Произвести минимизацию СНДФ методом Квайна – Мак-Класки. Построить таблицу истинности для полученной функции и сравнить с исходной.
Варианты задания 1. 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1
2.0 1 0 1 0 1 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 1 1 1
3.0 1 0 0 1 1 1 0 1 0 0 1 0 1 0 0 1 1 0 0 0 1 1 0 1 1 1 0 0 0 0 0 1 1 1 1
4.0 1 0 1 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 1 1 1 1
5.0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 1 1 1
6.0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
7.1 0 1 0 1 0 1 0 1 1 0 1 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 1
8.0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 1 0 1 1 0 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1
9.1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 1 1 1 0 0 0 0 1 1 1 1 1
10. 0 1 0 0 1 0 1 0 1 1 0 1 0 0 1 0 0 1 1 0 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1
11. 1 0 1 0 1 1 1 1 0 1 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1
12. 0 1 0 1 0 0 0 0 1 0 0 1 1 1 0 0 1 1 1 0 1 0 0 0 0 0 1 1
13. 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1
14. 1 1 1 1 1 0 1 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 0 1 1 1 1 0 0 0 0 1 1 1 1 1
15. 0 0 1 0 1 0 1 0 1 0 1 0 1 1 1 1 0 0 1 0 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1
16. 0 1 1 0 0 1 0 1 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 1
17. 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1
18. 0 0 1 1 1 0 1 1 0 0 1 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 1 0 0 0 0 0 1 1 1 1
19. 1 0 1 0 0 0 1 1 0 1 0 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1
20. 1 0 1 0 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1
21. 1 1 1 0 1 0 1 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 1 1 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1
22. 0 1 1 0 1 0 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 1 1 1 1
23. 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1
24. 1 0 1 0 1 0 1 0 1 1 0 1 1 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 1 1 0 0 0 0 0 0 1 1 1 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.209 (0.009 с.) |

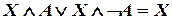 ;
; ;
; .
.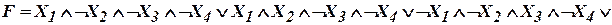
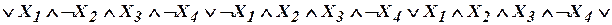
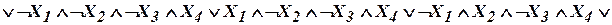
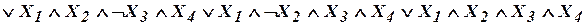 .
.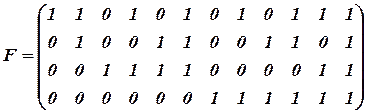 .
.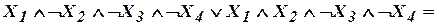
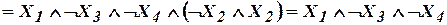 .
.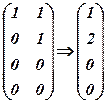 .
.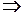 2; (1,0)
2; (1,0) 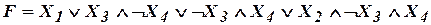 .
.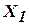 ,
, 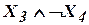 ,
,  и
и  . Для выяснения вопроса о минимальном покрытии строим таблицу импликант:
. Для выяснения вопроса о минимальном покрытии строим таблицу импликант: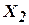

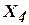
 .
.


