
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы сортировки и их классификацияСодержание книги
Поиск на нашем сайте Сортировка – это фактически неотъемлемая часть решения всех математических задач, заключающаяся в установлении линейного порядка на множестве. Примеры: составление списка студентов в журнале; список выигрышных билетов в лотерее. Постановка задачи. Имеется перетасованная колода карт, с каждой из которых сопоставлен ее порядковый номер. Требуется восстановить порядок. Алгоритм 1. Рассмотрим массив длиной 36. Берем карту из стопки и помещаем ее номер в первую позицию. Берем вторую карту. Если ее номер превышает номер помещенной позиции, то записываем во вторую позицию. В противном случае сдвигаем содержимое первой позиции во вторую, в первую позицию записываем номер взятой карты. Процесс повторяется, пока в колоде есть карты. Данный алгоритм называется «алгоритм вставок». Алгоритм 2. Рассмотрим алгоритм, эквивалентный приведенному, который заключается в следующем. Берем первую карту. Помещаем эту карту в позицию, номер которой совпадает с номером карты. Далее берем вторую карту и повторяем предыдущее действие. В этих двух алгоритмах результаты одинаковы. Рассмотрим в качестве критериальной функции количество перемещений содержимого ячеек в первом и во втором алгоритмах. Рассмотрим наилучший и наихудший случаи. Наилучший вариант: пусть исходная колода уже упорядочена, тогда количество перемещений содержимого равно нулю. Наихудший вариант: в колоде расположение обратное. По выбранному критерию первый алгоритм имеет эффективность Для реализации первого алгоритма можно построить вариант, при котором не нужна организация нового массива. Применение второго алгоритма связано с необходимостью выделения внешней памяти. Если ее нет или она очень дорого стоит, то второй алгоритм оказывается неприемлемым. Помимо алгоритма вставок, имеется большое количество алгоритмов внутренней сортировки, эквивалентных ему по значению критериальной функции. Пример: for i:=1 to n do for j:=1 to n do if a[i]>a[j] then begin c:=a[i]; a[i]=a[j]; a[j]=c; end; Алгоритм класса Пусть имеется два упорядоченных по возрастанию массива. Нужно получить массив из двух данных (упорядочить так же). Пусть имеется внешняя память. Основная идея: на каждом шаге перемещения осуществляются по тому из массивов, на вершине которого находится наименьший элемент. Перемещения сопровождаются записью этого элемента в новый массив и удалением его из того массива, в котором он располагался. Замечание. Необходимо предусмотреть дописывание «хвоста» – остатков того множества, которое было не пустым. Предложенный Дж. фон Нейманом алгоритм сортировки массива основывается на идее слияния. Количество операций при использовании этого алгоритма имеет порядок Рассмотрим первых два элемента массива, упорядочим их по возрастанию и заново запишем первые две позиции. Рассмотрим элементы, находящиеся на 3-й и 4-й позициях, упорядочим их по возрастанию и т.д. Если число элементов нечетное, то при окончании прохода по массиву нечетный элемент (последний) не изменяется. Шаги таковы: 1. Рассмотрим два массива (каждый длиной 2), которые расположены в 1-й и 2-й (первый массив) и 3-й и 4-й (второй массив) позициях. Оба массива упорядочены. Образуем массив длиной 4, он также упорядочен. Расположим его элементы в позициях 1, 2, 3, 4. Рассмотрим второй массив, элементы которого находятся в позициях 5, 6, 7, 8. Применим метод слияния и получим упорядоченный массив длиной 4. 2. Рассмотрим два массива (каждый длиной 4), расположенных в позициях 1, 2, 3, 4 и 5, 6, 7, 8. Образуем из них массив длиной 8. Записываем его элементы в позициях 1 – 8. 3. Рассмотрим первые две восьмерки, каждая из которых упорядочена. С помощью слияния образуем массив длиной 16 и т.д. Алгоритм остановится естественным путем. Замечание. Имеются и другие алгоритмы, применение которых требует примерно такого же количества операций сравнения. Это пирамидальная сортировка, двоичная сортировка. Их можно объединить в класс Другой класс образуют алгоритмы линейной сортировки. Примером является алгоритм ковшовой сортировки. Описание алгоритма ковшовой сортировки. Дан массив длиной 1. За один проход вычисляем наибольшее и наименьшее значения элементов массива. 2. Образуем внешний массив с той же длиной. Каждый элемент этого массива имеет тип – указатель. 3. Последовательно просматриваем исходный массив. Пусть появилось некоторое значение
Во внешнем массиве рассматривается элемент с номером 4. В каждом ковше образуется список номеров элементов, попавших в данный ковш. Упорядочиваем элементы внутри каждого из ковшей любым из простейших способов. 5. Читаем внешний массив последовательно. Пример:
Некоторые из черпаков (ковшей) оказываются пустыми. Для оценивания количества операций отметим, что в каждом из черпаков окажется в среднем по одному элементу. Упорядочение внутри одного черпака потребует в среднем одно действие. Поэтому общее количество операций будет иметь порядок Поиск Важной разновидностью алгоритмов является множество алгоритмов поиска в линейной структуре. Задача поиска ставится так: установить, принадлежит ли некий элемент множеству Простейший алгоритм заключается в сравнении Этот простейший алгоритм можно отнести к классу Можно ли уменьшить количество операций сравнения? Ответ положителен, если использовать следующие действия: – упорядочение исходной структуры; – применение дихотомии (половинного деления). Пример. Задан упорядоченный массив
Рассмотрим число Этапы дихотомии таковы. Пусть имеются восемь элементов, упорядоченных по возрастанию, делим 8 пополам, возникает номер 4. Сравниваем числа Предположим, что
Рассмотрим средний номер в полученной последовательности. Сравниваем
Сравниваем Предположим, что Замечание. Количество элементов может и не быть равным БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Карпов Ю.Г. Теория автоматов / Ю.Г. Карпов. – СПб.: Питер, 2003. – 206 с. 2. Новиков Ф.А. Дискретная математика для программистов / Ф.А. Новиков. – СПб.: Питер, 2000. – 304 с. 3. Чернышев Ю.К. Решение основных задач теории графов с помощью ЭВМ / Ю.К. Чернышев. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2008. – 78 с. 4. Колодяжный В.М. Введение в дискретную математику: учеб. пособие: в 2 ч. / В.М. Колодяжный, И.Б. Сироджа. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 1999. – Ч. 2. – 204 с. 5. Трохимчук Р.М. Основи дискретної математики / Р.М. Трохимчук. – К.: МАУП, 2004. – 164 с. 6. Липский В. Комбинаторика для программистов / В. Липский. – М.: Мир, 1988. – 214 с. 7. Информатика / А.В. Карташов, Ю.А. Скоб, В.А. Халтурин и др. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2005. – 178 с.
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.. 3 1. БУЛЕВЫ ФУНКЦИИ.. 4 1.1. Определение булевых функций. 4 1.2. Построение СНДФ, СНКФ и СНПФ. Минимизация. 9 1.3. Реализация метода Квайна – Мак-Класки. 12 1.4. Замкнутые классы. Полнота. Теорема Поста. 17 1.5. Моделирование релейно-контактных схем.. 19 1.6. Моделирование сумматоров. 22 2. ОСНОВНЫЕ ПОЛОЖЕНИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.. 26 2.1. Формальные теории. 26 2.2. Исчисление высказываний. 27 2.3. Исчисление предикатов. 32 2.4. Приложение исчисления предикатов к аналитической геометрии 35 3. ВЫЧИСЛИМОСТЬ.. 37 3.1. Неформальное определение алгоритма. Примеры.. 37 3.2. МНР-вычислимые функции. 37 3.3. Рекурсия. 37 3.4. Вычислимость по Тьюрингу. 37 4. КОНЕЧНЫЕ АВТОМАТЫ.. 37 4.1. Основные определения и способы задания. 37 4.2. Эквивалентность автоматов. Минимизация. 37 4.3. Автоматы Мили и Мура. Размеченные графы.. 37 4.4. Автоматные языки. 37 4.5. Возможности автоматов. 37 5. НЕКОТОРЫЕ КЛАССИЧЕСКИЕ АЛГОРИТМЫ.. 37 5.1. Алгоритмы сортировки и их классификация. 37 5.2. Поиск. 37 БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 37
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

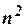 , второй – 1.
, второй – 1. .
. -эквивалентных алгоритмов.
-эквивалентных алгоритмов. . Требуется упорядочить его по возрастанию.
. Требуется упорядочить его по возрастанию. . Вычисляем номер ковша
. Вычисляем номер ковша .
. (т.е. ковш с номером
(т.е. ковш с номером  ;
; 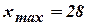 ;
; .
. с
с 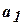 ,
,  и т.д. пока либо будет зарегистрировано равенство
и т.д. пока либо будет зарегистрировано равенство  , либо номер
, либо номер  .
. .
.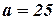 .
. .
. . Нужны ли после этого предыдущие элементы? Ясно, что не нужны. Исходный массив в данном примере уменьшается вдвое:
. Нужны ли после этого предыдущие элементы? Ясно, что не нужны. Исходный массив в данном примере уменьшается вдвое: :
:  . Следовательно,
. Следовательно, . Получаем равенство
. Получаем равенство 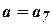 . Вывод: заданное число содержится в исходном массиве.
. Вывод: заданное число содержится в исходном массиве. . Тогда поиск с помощью указанного алгоритма приведет к противоречию.
. Тогда поиск с помощью указанного алгоритма приведет к противоречию. , в таком случае при делении пополам следует брать целую часть.
, в таком случае при делении пополам следует брать целую часть.


