
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наближенні рішення рівнянь Максвела для круглих слоїстих світловодів.Содержание книги
Поиск на нашем сайте
переходит в уравнение Гельмгольца: где χ - поперечное волновое число, или собственное значение; β- фазовая постоянная.
для сердцевины ОВ с показателем преломления п1в виде:
а для оболочки с п2, в виде:
решения (2.54) и (2.55) дают возможность изучить условия распространения волн в ступенчатом ОВ. В решениях (2.54) и (2.55) Ат Вт Ст и Dm - постоянные интегрирования; Jn, Nn - функции Бесселя первого и второго рода п-то порядка, соответственно; In и Кn — видоизмененные (модифицированные) функции Бесселя первого и второго рода и-го порядка, соответственно.
Постоянные интегрирования Ат и Dm могут быть определены на основании граничных условий. Поперечные составляющие электрических Еr Еφ и магнитных Нr, Нφ полей могут быть выражены с помощью известных соотношений между поперечными и продольными Ez, Hz составляющими. Тогда, используя условие равенства тангенцианальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина - оболочка (при r=а):
найдем постоянные интегрирования. Подставим их в уравнения типа (2.56) и (2.57), и после соответствующих преобразований получим следующее характеристическое уравнение:
Это уравнение позволяет определить структуру поля, параметры волн и характеристики ОВ. В общем случае оно имеет ряд решеняй, каждому из которых соответствует определенная структура поля, называемая типом волны, или модой. Обычно в ступенчатых ОВ, применяемых для линий передачи сигналов, п1
В ступенчатом ОВ отсечка моды (критические условия) наступает при равенстве поперечного волнового числа в оболочке –a2=0, это возможно при β =k2- При этом условии из (2.60) следует, что
(2.61)
В приведенных обозначениях мод первый индекс учитывает порядок функции, второй -номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя. Следующая совокупность мод соответствует n= 1 или характеристическому уравнению:J0(χ1r)=0 Первым корнем этого уравнения является χ1а = 2,405. Ему соответствуют две волны Н01и Е01.. Второму корню уравнения соответствует следующая пара мод Н02 и Е02 и т.д.Таким образом, функции Бесселя первого рода n-го порядка дают бесконечное число корней. Причем корни функции:J0(χ1a) определяют структуру поля симметричных волн (Е0m H0m), a Jn(χ1a) при n Все составляющие эл/магн поля в волноводе обычно опр-ют через сост-щие
Область разрешенных значений постоянных распространения
31. Дисперсійні залежності ВС зі ступінчатим профілем показника заломлення Дисперсионные характеристики для нескольких первых мод в волоконном световоде со ступенчатым профилем приведены на рис. 1.5. Область разрешенных значений постоянной распространения р зависит от значений показателя преломления сердечника и оболочки: n2 ≤β/k≤n1. Равенство β/k = n2 представляет собой условие частот отсечки. На частоте отсечки поле выходит из сердечника световода. Частота отсечки основной моды НЕ11 равна нулю. Мода НЕ11 является двукратно вырожденной по поляризации, так как в круглом световоде все ориентации вектора Е эквивалентны, вследствие чего могут существовать моды со взаимно перпендикулярной поляризацией и одинаковым волновым числом. Эллиптичность сердечника приводит к снятию этого вырождения.
2,405 > (2πα/λ) (n12- n22) 1/2 = V.(1.5) Из анализа выражения (1.5) видно, что для увеличения размеров сердечника круглого световода в одномодовом режиме желательно брать малое значение разности показателей преломления. Поэтому на практике используют световоды с малой разностью показателей преломления сердечника и оболочки: Δ1 = n1 - n2 = 0,005…0,03. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия, достигающая больших значений (20…50 нс/км) В одномодовых ступенчатых световодах отсутствует модовая дисперсия. Здесь проявляется волноводная и материальная дисперсия, но они почти равны по абсолютной величине и противоположны по фазе в широком спектральном диапазоне в силу этого происходит их взаимная компенсация и результирующая дисперсия при
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.201 (0.009 с.) |

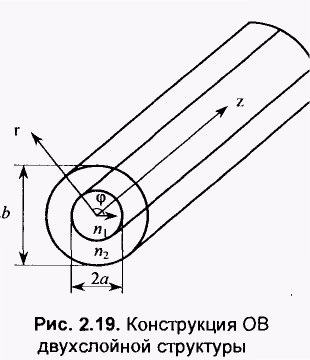 Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения. Волновое уравнение в цилиндрической системе координат г, φ, z относительно компонентов электрического поля или магнитного поля Hz, изменяющихся во времени t и вдоль оси z волокна, в виде
Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения. Волновое уравнение в цилиндрической системе координат г, φ, z относительно компонентов электрического поля или магнитного поля Hz, изменяющихся во времени t и вдоль оси z волокна, в виде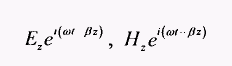
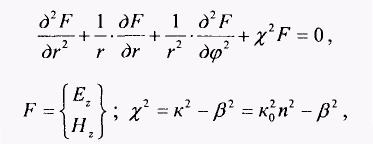 Для описания поведения электромагнитного поля в сердцевине (0<r<а) и в оболочке (a <r <b) необходимо использовать различные функции. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с п2 на рис. 2.19 простирается до бесконечности (d=oo). В таком случае п в формуле (2.52) равно или n1 в середине ОВ, или п2 во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить
Для описания поведения электромагнитного поля в сердцевине (0<r<а) и в оболочке (a <r <b) необходимо использовать различные функции. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с п2 на рис. 2.19 простирается до бесконечности (d=oo). В таком случае п в формуле (2.52) равно или n1 в середине ОВ, или п2 во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить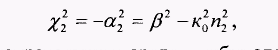 чтобы поле в радиальном направлении в среде и, убывало. Тогда решение уравнения Гельмгольца можно записать:
чтобы поле в радиальном направлении в среде и, убывало. Тогда решение уравнения Гельмгольца можно записать: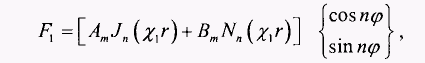 2.54
2.54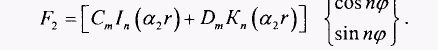 (2.55)
(2.55)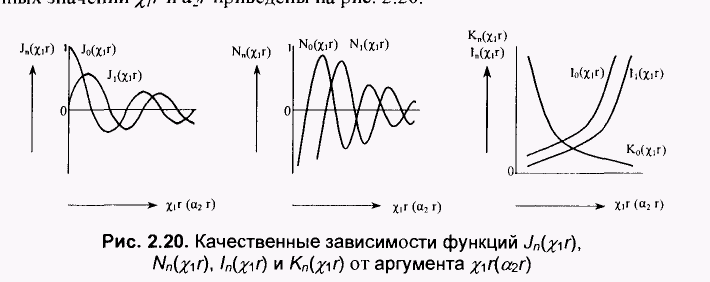
 При r—>0 значение Nn—> -со. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить Вт=0. Поле за пределами сердцевины должно убывать в радиальном направлении и при г—>оо должно стремиться к нулю. Однако In при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить С„= 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция Jn(χ1r) описывает распределение поля внутри сердцевины ОВ, а функция Кп(а2r) описывает изменение поля за ее пределами (в среде с п2) и ведет себя при больших значениях а2г как ехр(-а2r). Тогда уравнения (2.54) и (2.55) перепишутся в виде(2.56 2.57):==================================
При r—>0 значение Nn—> -со. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить Вт=0. Поле за пределами сердцевины должно убывать в радиальном направлении и при г—>оо должно стремиться к нулю. Однако In при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить С„= 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция Jn(χ1r) описывает распределение поля внутри сердцевины ОВ, а функция Кп(а2r) описывает изменение поля за ее пределами (в среде с п2) и ведет себя при больших значениях а2г как ехр(-а2r). Тогда уравнения (2.54) и (2.55) перепишутся в виде(2.56 2.57):================================== (2.58)
(2.58)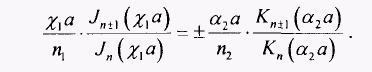 (2.59)
(2.59) п2. Тогда уравнение (2.59) можно переписать в виде:
п2. Тогда уравнение (2.59) можно переписать в виде: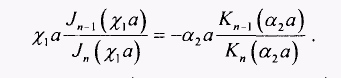 (2.60)
(2.60)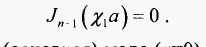
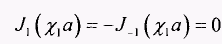 Отсюда видно, что низшая основная мода (п=0) имеет отсечку, определяемую из уравнения:
Отсюда видно, что низшая основная мода (п=0) имеет отсечку, определяемую из уравнения: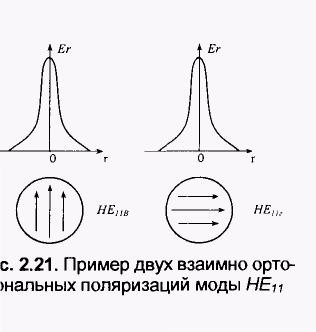 Первый корень этого характеристического уравнения χ1а = 0, и он соответствует моде НЕ11. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ11rг и НЕ11в, соответствующих cos φ и sin φ.(2.21). Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J1(χ1r) второй раз становится равной нулю, т.е. когда χ1a=3,83. Эта мода обозначается НЕ12. Aналогично для n = 0 следуют моды НЕ13, НЕ14….
Первый корень этого характеристического уравнения χ1а = 0, и он соответствует моде НЕ11. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ11rг и НЕ11в, соответствующих cos φ и sin φ.(2.21). Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J1(χ1r) второй раз становится равной нулю, т.е. когда χ1a=3,83. Эта мода обозначается НЕ12. Aналогично для n = 0 следуют моды НЕ13, НЕ14….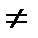 0 структуру несимметричных гибридных волн (ЕНnm, НЕnm). В индексе моды n - число изменений поля по диаметру, a m- число изменений поля по периметру сердцевины ОВ.
0 структуру несимметричных гибридных волн (ЕНnm, НЕnm). В индексе моды n - число изменений поля по диаметру, a m- число изменений поля по периметру сердцевины ОВ. и
и 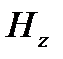 :
:


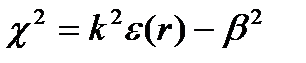
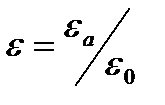 -относ. диэлектрич. проницаемость среды; n – пок - ль преломления
-относ. диэлектрич. проницаемость среды; n – пок - ль преломления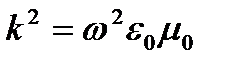 ,
,  -круговая частота;
-круговая частота; 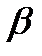 -продольная постоянная распространения
-продольная постоянная распространения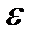 на длине волны можно считать
на длине волны можно считать 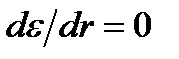 . При этом система распадается на независимых однородных диф. уравнения второго порядка:
. При этом система распадается на независимых однородных диф. уравнения второго порядка: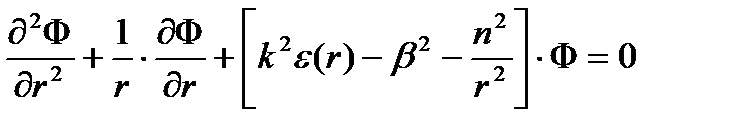 , где
, где 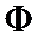 -ф-ия пропорциональная
-ф-ия пропорциональная  - дисперс. хар-ку моды.
- дисперс. хар-ку моды.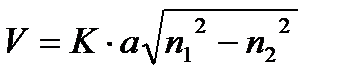 - нормированная частота.
- нормированная частота.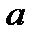 - радиус сердечника.
- радиус сердечника.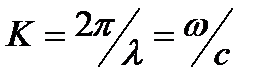 - волновое число в свободном пространстве.
- волновое число в свободном пространстве.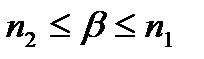 . Равенство
. Равенство 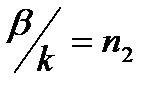 -условия частоты отсечки. На ч-те отсечки поле выходит из серд-ка световода. Ч-та отсечки осн. моды HE11 равна нулю. Мода HE11 - двукратно вырожденная по поляризации, т.к. в круглом световоде все ориентации вектора Е эквивалентны, вследствии чего могут сущ-ть моды со взаимно перпендикул. поляризацией и одинаковым волновым числом. Эллиптичность сердечника приводит к снятию данного вырождения. Если на заданной раб. ч-те параметры световода выбрать так, чтобы следующие высшие моды ТE01, ТМ01, HE21 с более высокими ч-ми отсечки не могли распр-ся, то получим одномодовый световод.В этом случае должно вып-ться условие одномодовости:
-условия частоты отсечки. На ч-те отсечки поле выходит из серд-ка световода. Ч-та отсечки осн. моды HE11 равна нулю. Мода HE11 - двукратно вырожденная по поляризации, т.к. в круглом световоде все ориентации вектора Е эквивалентны, вследствии чего могут сущ-ть моды со взаимно перпендикул. поляризацией и одинаковым волновым числом. Эллиптичность сердечника приводит к снятию данного вырождения. Если на заданной раб. ч-те параметры световода выбрать так, чтобы следующие высшие моды ТE01, ТМ01, HE21 с более высокими ч-ми отсечки не могли распр-ся, то получим одномодовый световод.В этом случае должно вып-ться условие одномодовости: 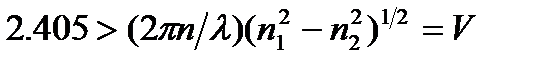 . Из анализа выр-я видно, что для увеличения размеров сердечника круглого световода в одномодовом режиме желательно брать малое значение разности пок-лей преломления. Поэтому на практике беруться световоды с малой разностью пок-лей преломления сердечника и оболочки
. Из анализа выр-я видно, что для увеличения размеров сердечника круглого световода в одномодовом режиме желательно брать малое значение разности пок-лей преломления. Поэтому на практике беруться световоды с малой разностью пок-лей преломления сердечника и оболочки 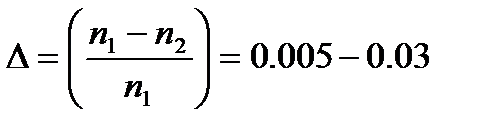
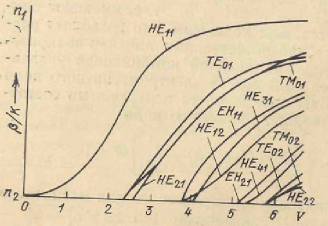 Если на заданной рабочей частоте параметры световода выбрать так, чтобы следующие высшие моды ТЕ01, ТМ01 НЕ21 с более высокими частотами отсечки не могли распространяться, то получим одномодовый световод, т. е. световод с одной только распространяющейся модой НЕ11. В этом случае должно выполняться условие одномодовости
Если на заданной рабочей частоте параметры световода выбрать так, чтобы следующие высшие моды ТЕ01, ТМ01 НЕ21 с более высокими частотами отсечки не могли распространяться, то получим одномодовый световод, т. е. световод с одной только распространяющейся модой НЕ11. В этом случае должно выполняться условие одномодовости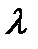 = 1,2…1.7 мкм не превышает 1 нс/км.
= 1,2…1.7 мкм не превышает 1 нс/км.


