Bump Mapping/Specular Bump Mapping

 

Бампмаппинг — это техника симуляции неровностей (или моделирования микрорельефа, как больше нравится) на плоской поверхности без больших вычислительных затрат и изменения геометрии, он был разработан Блинном (Blinn) еще в 1978 году. Человек зрительно воспринимает неровности на поверхностях благодаря характерному их освещению. Для каждого пикселя поверхности выполняется вычисление освещения, исходя из значений в специальной карте высот, называемой bump map. Обычно это 8-битная черно-белая текстура. Цвет каждого ее текселя определяет высоту соответствующей точки рельефа, большие значения означают большую высоту над исходной поверхностью, а меньшие, соответственно, меньшую (или наоборот).

Степень освещенности точки зависит от угла падения лучей света. Чем меньше угол между нормалью и лучом света, тем больше освещенность точки поверхности. То есть, если взять ровную поверхность, то нормали в каждой ее точке будут одинаковыми и освещенность также будет одинаковой. А если поверхность неровная (собственно, как практически все поверхности в реальности), то нормали в каждой точке будут разными. И освещенность разная, в одной точке она будет больше, в другой — меньше. Отсюда и принцип бампмаппинга — для моделирования неровностей для разных точек полигона задаются нормали к поверхности, которые учитываются при вычислении попиксельного освещения. В результате получается более натуральное изображение поверхности: бампмаппинг дает поверхности большую детализацию, такую, как неровности на кирпиче, поры на коже и т.п., без увеличения геометрической сложности модели, так как расчеты ведутся на пиксельном уровне. Причем, при изменении положения источника света освещение этих неровностей правильно изменяется.

Конечно, вершинное освещение намного проще вычислительно, но оно слишком нереалистично выглядит, особенно при сравнительно малополигональной геометрии. Интерполяция цвета для каждого пикселя не может воспроизвести значения, большие, чем рассчитанные значения для вершин. То есть, пиксели в середине треугольника не могут быть ярче, чем пиксели возле вершины. Следовательно, области с резким изменением освещения, такие как блики и источники света, очень близко расположенные к поверхности, будут физически неправильно отображаться, и особенно это будет заметно в динамике. Конечно, частично проблема решаема увеличением геометрической сложности модели, ее разбиением на большее количество вершин и треугольников, но оптимальным вариантом будет попиксельное освещение.

Для продолжения необходимо напомнить о составляющих освещения. Цвет точки поверхности рассчитывается как сумма ambient (фоновой), diffuse (рассеянной), emission (излученной) и specular (бликовой) составляющих от всех источников света в сцене (в идеале от всех, зачастую многими пренебрегают). Вклад в это значение от каждого источника света зависит от расстояния между источником света и точкой на поверхности.

Продемонстрируем все это:

 

А теперь добавим к этому бампмаппинг:

Фоновая (ambient) составляющая освещения — приближение глобального освещения, «начального» освещения для каждой точки сцены, при котором все точки освещаются одинаково и освещенность не зависит от других факторов.

Рассеянная (diffuse) составляющая освещения зависит от положения источника освещения и от нормали поверхности. Эта составляющая освещения разная для каждой вершины объекта, что придает им объем. Свет уже не заполняет поверхность одинаковым оттенком.

Бликовая (specular) составляющая освещения проявляется в бликах отражения лучей света от поверхности. Для ее расчета, помимо вектора положения источника света и нормали, используются еще два вектора: вектор направления взгляда и вектор отражения. Specular модель освещения впервые предложил Фонг (Phong Bui-Tong). Эти блики существенно увеличивают реалистичность изображения (редкие реальные поверхности не отражают свет), поэтому эта составляющая очень важна, особенно в движении, потому что по бликам сразу видно изменение положения камеры или самого объекта. В дальнейшем, исследователи придумывали иные способы вычисления этой составляющей, более сложные (Blinn, Cook-Torrance, Ward), учитывающие распределение энергии света, его поглощение и рассеивание.

Итак, Specular Bump Mapping получается таким образом:

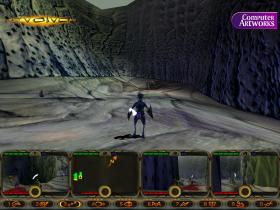
И то же самое на примере игры, Call of Duty 2:

Первый фрагмент картинки — рендеринг без бампмаппинга вообще, второй (вверху справа) — бампмаппинг без бликовой составляющей, третий — с бликовой составляющей нормальной величины, какая используется в игре, и последний, внизу справа — с ее максимально возможным значением.

Что касается первого аппаратного применения, то некоторые виды бампмаппинга (Emboss Bump Mapping) стали использовать еще во времена видеокарт на базе чипов NVidia Riva TNT, однако техники того времени были крайне примитивны и широкого применения не получили. Следующим известным типом стал Environment Mapped Bump Mapping (EMBM), но аппаратной его поддержкой в DirectX в то время обладали только видеокарты Matrox, и опять применение было сильно ограничено. Затем появился Dot3 Bump Mapping, и видеочипы того времени (GeForce 256 и GeForce 2) требовали три прохода для того, чтобы полностью выполнить такой математический алгоритм, так как они были ограничены двумя одновременно используемыми текстурами. Начиная с NV20 (GeForce3), появилась возможность делать то же самое за один проход при помощи пиксельных шейдеров. Дальше — больше. Стали применять более эффективные техники, такие как Normal Mapping. Примеры применения бампмаппинга в играх:

Normal Mapping

 

Нормалмаппинг — это улучшенная разновидность описанной ранее техники бампмаппинга, ее расширенная версия. В то время как бампмаппинг изменяет существующую нормаль, исходя из высоты точки поверхности, нормалмаппинг полностью заменяет нормали при помощи выборки их значений из специально подготовленной карты нормалей (normal map). Эти карты обычно являются текстурами с сохраненными в них заранее просчитанными значениями нормалей, представленными в виде компонент цвета RGB (впрочем, есть и специальные форматы для карт нормалей, в том числе со сжатием).

В общем, как и бампмаппинг, это тоже «дешевый» метод добавления детализации к моделям сравнительно низкой геометрической сложности без использования большего количества реальной геометрии, только более продвинутый. Одно из наиболее интересных применений техники — существенное увеличение детализации низкополигональных моделей при помощи карт нормалей, полученных обработкой такой же модели высокой геометрической сложности. Карты нормалей содержат более подробное описание поверхности, по сравнению с бампмаппингом, и позволяют представить более сложные формы (из любой карты высот можно получить карту нормалей, но не каждой карте нормалей можно поставить в соответствие карту высот). Идеи по получению информации из высокодетализированных объектов были озвучены в середине 90-х годов прошлого века, но тогда речь шла об использовании для Displacement Mapping. Позднее, в 1998 году, были представлены идеи о перенесении деталей в виде карт нормалей от высокополигональных моделей в низкополигональные.

Единственное серьезное ограничение нормалмаппинга состоит в том, что он не очень хорошо подходят для крупных деталей, ведь на самом деле форму объекта не изменяется, и это будет заметно, особенно на крайних полигонах объекта и при больших углах наклона поверхности. Поэтому наиболее разумный способ применения нормалмаппинга состоит в том, чтобы сделать низкополигональную модель достаточно детализированной для того, чтобы сохранялась основная форма объекта, и использовать карты нормалей для добавления еще более мелких деталей.

Карты нормалей обычно создаются на основе двух версий модели, низко- и высокополигональной. Низкополигональная модель состоит из минимума геометрии, основных форм объекта, а высокополигональная содержит все необходимое для максимальной детализации. Затем при помощи специальных утилит они сравниваются друг с другом, разница рассчитывается и сохраняется в текстуре — той самой карте нормалей. При ее создании дополнительно можно использовать и bump map для очень мелких деталей, которые даже в высокополигональной модели не смоделировать (поры кожи, другие мелкие углубления).

Карты нормалей изначально были представлены в виде обычных RGB текстур, где компоненты цвета R, G и B (от 0 до 255) интерпретируются как координаты X, Y и Z. Каждый тексель в карте нормалей будет представлен как нормаль в этой точке поверхности. Карты нормалей могут быть двух видов: с координатами в model space (общей системе координат) или tangent space (термин на русском — «касательное пространство», локальная система координат треугольника), чаще применяется второй вариант. В представлении model space карты нормалей должны иметь три компоненты, так как могут встретиться все направления, а в tangent space можно обойтись двумя компонентами, а третью рассчитать в пиксельном шейдере.

Техника нормалмаппинга сейчас применяется почти повсеместно, все новые игры используют ее максимально широко. Все они выглядят намного лучше, чем игры прошлого, в том числе из-за применения карт нормалей. Примеры:

Ну что, заинтриговал? Захотелось реализовать бампмаппинг в сцене? Тогда приступим:

Реализация в GLScene

 

Возможно использовать данный шейдер тремя способами: через стандартный компонент GLBumpShader, через стандартный GLSLBumpShader, либо вообще обойтись без компонентов. Здесь мы рассмотрим только первый способ.

Итак, поместим на форму GLScene (инспектор объектов сцены), в нём создадим источник света и камеру (ее Position.Z = 5). Создаем GLSceneViewer, свойству Camera присваиваем нашу камеру (всё как обычно, ничего нового).

Затем создадим GLBumpShader (вкладка GLScene Shaders) и GLMaterialLibrary с двумя материалами. Один назовём Bump_mat (сюда будем загружать рельеф), другой mat (сюда будем загружать обычную текстуру). Присваиваем свойству Texture2Name (вспомогательная текстура) материала Bump_mat значение mat. Загружаем в mat любую текстуру, а в Bump_mat карту нормалей. Вопрос, как её получить? Самое легкое — назначить этому материалу в GLScene для свойства Object.Material.Texture.TextureFormat значение tfNormalMap. Это можно сделать как в design time, так и в runtime. Второй метод хорош, если вам требуется дополнительно обработать текстуру, осуществив, например, тайлинг — нужен плагин для фотошопа от NVidia. Как с ним работать описано здесь: http://www.uraldev.ru/articles/id/31. Если нужно просто попробовать, можно взять нормал текстуры из интернета, например, отсюда: http://www.itcommunity.ru/blogs/timofeevdmitry/archive/2009/6/15.aspx (берите синеватое изображение). Возвращаемся в сцену. Присвойте свойству Shader материала Bump_mat наш GLBumpShader и установите значение Material.Texture.Disabled обоих материалов в False.

Далее создадим в GLScene объект GLPlane (на него будем натягивать бамп), свойству MaterialLibrary присвоим значению GLMaterialLibrary1 (нашу библиотеку материалов), свойству LibMaterialName присвоим Bump_mat. Почти готово — можно запускать! Когда запустите, увидите, что картинка чёрно-белая — нужно, чтобы в свойстве GLBumpShader. BumpOptions присутствовало значение boDiffuseTexture2.

Есть лишь одно негативное последствие применения этой техники — увеличение объемов текстур. Ведь карта нормалей сильно влияет на то, как будет выглядеть объект, и она должна быть достаточно большого разрешения, поэтому требования к видеопамяти и ее пропускной способности удваиваются (в случае несжатых карт нормалей). Но сейчас уже выпускаются видеокарты с 1024 мегабайтами локальной памяти, их пропускная способность постоянно растет, разработаны методы сжатия специально для карт нормалей, поэтому эти небольшие ограничения не слишком важны. Гораздо важнее, что можно получить весьма достойный визуальный результат используя сравнительно низкополигональные модели.