
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конденсатори. Електроємність конденсатора. З’єднання конденсаторівСодержание книги
Поиск на нашем сайте
Здатність провідника накопичувати електричний заряд характеризується його електроємністю, вона пропорційна до розмірів провідника. Однак електроємність навіть великого за розміром провідника є малою і недостатньою для практичного використання. Розглянемо систему двох провідників розділених діелектриком, яку будемо називати конденсатором. Зарядимо кожен із провідників рівними за величиною і протилежними за знаком зарядами. Це рівнозначно перенесенню деякого електричного заряду з одного провідника (обкладки конденсатора) на інший. Внаслідок взаємного притягання між протилежними за знаком зарядами обкладок конденсатора кожен із провідників конденсатора має значно більшу накопичувальну здатність, ніж відокремлений провідник. Тому електроємність конденсатора є значно більшою, ніж електроємність відокремленого провідника. Електроємністю конденсатора називається фізична величина, рівна зарядові, який необхідно перенести з однієї обкладки на іншу, щоб різниця потенціалів між ними змінилась на одиницю
де За формою обкладок конденсатори поділяють на плоскі, циліндричні і сферичні.
Напруженість електричного поля між обкладками рівна
де
Різницю потенціалів знайдемо за формулою (3.73)
Підставляючи (3.102) в (3.99), одержимо формулу електроємності плоского конденсатора
Напруженості електричного поля ззовні від конденсатора, створеного однією та іншою обкладками, взаємно компенсуються. Тому результуюча напруженість електричного поля ззовні від конденсатора рівна нулю.
Напруженість електричного поля всередині внутрішнього циліндра рівна нулю, оскільки електричне поле всередині провідника відсутнє. Напруженість електричного поля в просторі між циліндрами створюється лише зарядом внутрішнього циліндра і рівна Напруженість електричного поля ззовні від циліндра радіусом Різницю потенціалів між обома циліндрами знайдемо за формулою (3.89)
де
Підставимо (3.105) в (3.104)
Підставимо (3.106) у формулу (3.99) і одержимо формулу електроємності циліндричного конденсатора
Напруженість електричного поля всередині внутрішнього сферичного провідника рівна нулю. Напруженість електричного поля в просторі між сферичними провідниками створюється лише зарядом внутрішньої кулі і рівна Напруженість електричного поля ззовні від сферичного провідника радіусом
Підставимо (3.108) у формулу (3.99) і одержимо формулу електроємності сферичного конденсатора
Для практичних потреб конденсатори часто з’єднують між собою в батареї. Найбільш поширеними є паралельне і послідовне з’єднання конденсаторів. Розглянемо паралельне з’єднання конденсаторів при якому позитивно заряджені обкладки всіх конденсаторів з’єднують в один полюс, а негативно заряджені обкладки – в інший полюс (рис.3.22). При паралельному з’єднанні конденсаторів напруга на всіх конденсаторах однакова, а заряд батареї конденсаторів рівний серії зарядів на кожному з них
Підставивши (3.110) і (3.111) у формулу (3.99), одержимо формулу електроємності при паралельному з’єднанні конденсаторів
При послідовному з’єднанні конденсаторів заряди всіх конденсаторів однакові, а напруга батареї конденсаторів рівна сумі напруг на кожному із них
Підставивши (3.113) і (3.114) у формулу (3.99), одержимо формулу електроємності при послідовному з’єднанні конденсаторів
Електричний струм. Закон Ома для ділянки кола. Закон Ома в диференціальній формі Серед великої кількості електричних явищ важливе наукове, теоретичне і практичне значення, мають явища пов’язані із переміщенням електричних зарядів, тобто електричним струмом. Електричним струмом називається впорядковане переміщення електричних зарядів. Для існування електричного струму необхідно, щоб в середовищі були вільні електричні заряди і щоб в середовищі існувало електричне поле. Речовини, які містять вільні електричні заряди здатні переміщуватись по всьому об’єму тіла під дією електричного поля називаються провідниками. Вільні електричні заряди в провідниках називаються носіями струму. Носіями електричного струму в металах є електрони, в електролітах – позитивно й негативно заряджені іони, в газах – електрони та іони. За напрямок струму приймається напрямок переміщення позитивних зарядів. Силою струму називається скалярна фізична величина, рівна зарядові, який проходить через поперечний переріз провідника за одиницю часу
У випадку постійного струму сила струму рівна
Одиницею вимірювання сили струму в системі одиниць СІ є ампер (А). Ця одиниця є однією із основних в системі СІ. Для характеристики розподілу електричного струму по перерізу провідника і його напрямку в просторі користуються поняттям густини струму.Густиною струму називається векторна фізична величина, яка чисельно рівна силі струму, який проходить через одиничний поперечний переріз провідника, перпендикулярний до напрямку струму і має напрямок швидкості позитивно заряджених частинок
У випадку однорідного струму модуль густини струму рівний
В процесі проходження електричного струму сили електричного поля виконують деяку роботу по переміщенню заряду. Однак, електричні заряди можуть переміщуватись і під дією сил іншої природи або сторонніх сил. Для характеристики цієї роботи використовується поняття електричної напруги. Електричною напругою на ділянці кола називається скалярна фізична величина, яка рівна роботі електричних і сторонніх сил по переміщенню одиничного позитивного заряду на цій ділянці
У випадку постійного струму напруга рівна
Одиницею вимірювання електричної напруги в системі одиниць СІ є вольт (В). Один вольт рівний напрузі при якій виконується робота в 1Дж при переміщенні електричного заряду 1Кл на даній ділянці кола. Німецький фізик Г.Ом експериментально відкрив закон, який встановлює зв’язок між силою струму в провіднику і напругою на його кінцях
де Формула (3.162) – це закон Ома для однорідної ділянки кола: сила струму в провіднику прямо пропорційна прикладеній напрузі і обернено пропорційна опору провідника. Опір провідника характеризує здатність провідника перешкоджати проходженню по ньому струму за рахунок перетворення енергії струму у внутрішню енергію провідника. Одиницею вимірювання опору є Ом. Один Ом це опір такого провідника по якому протікає струм силою 1А при прикладеній напрузі 1В. Величина обернена до електричного опору називається електричною провідністю провідника
Одиницею вимірювання провідності є Сіменс (См). Один Сіменс рівний електричній провідності провідника опором 1Ом. Електричний опір провідника залежить від його геометричних розмірів і матеріалу, з якого виготовлений провідник
де
Опір і питомий опір металевого провідника є лінійною функцією температури
При температурі близькій до абсолютного нуля опір деяких провідників стає рівним нулю. Це явище називається надпровідністю. Воно було відкрите Камерлінг-Онессом у 1911 р. Якщо в замкнутому колі складеному з надпровідника, створити електричний струм, то він циркулюватиме тривалий час практично не зменшуючись протягом тижнів і місяців. Виділимо в провіднику елементарний циліндр довжиною Тоді формули (3.162) і (3.164) наберуть вигляду
Підставимо (3.169) в (3.168) і використаємо (3.158), дістанемо
Врахуємо, що
Підставимо (3.171) у вираз (3.170):
Формули (3.172) можна представити також у векторній формі
Формули (3.173) – це закон Ома в диференціальній формі для однорідної ділянки кола. В ізотропному провіднику носії струму в кожній точці рухаються в напрямку вектора Оскільки напрямлений рух носіїв струму створюється електричним полем в провіднику, то можна вважати, що середня швидкість
де коефіцієнт пропорційності Виразимо силу і густину струму через середню швидкість
де
Підставимо вираз (3.176) у формулу (3.159) отримаємо формулу густини струму
Підставимо вираз (3.174) у формулу (3.177), дістанемо
Порівняємо формулу (3.178) із виразом (3.172). Отримаємо формулу питомої електропровідності речовини
Отже, питома електропровідність провідника прямо пропорційна електричному зарядові носія струму, рухливості носіїв і їх концентрації.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.007 с.) |

 , (3.99)
, (3.99) і
і  – потенціали обкладок,
– потенціали обкладок,  – різниця потенціалів.
– різниця потенціалів. Розглянемо плоский конденсатор, який складається з двох плоских паралельних обкладок площею
Розглянемо плоский конденсатор, який складається з двох плоских паралельних обкладок площею 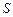 кожна, які знаходяться на відстані
кожна, які знаходяться на відстані  одна від одної (рис. 3.19). Нехай між обкладками міститься діелектрик з діелектричною проникністю
одна від одної (рис. 3.19). Нехай між обкладками міститься діелектрик з діелектричною проникністю  і обкладки заряджені зарядами
і обкладки заряджені зарядами  і
і  .
. , (3.100)
, (3.100) і
і 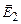 – напруженості полів, створених кожною з обкладинок. Будемо вважати розміри обкладок конденсатора значно більшими ніж відстань між ними. Тоді величини
– напруженості полів, створених кожною з обкладинок. Будемо вважати розміри обкладок конденсатора значно більшими ніж відстань між ними. Тоді величини  і
і 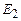 можемо визначити за формулою (3.55) напруженості електричного поля створеного нескінченою рівномірно зарядженою площиною
можемо визначити за формулою (3.55) напруженості електричного поля створеного нескінченою рівномірно зарядженою площиною . (3.101)
. (3.101) . (3.102)
. (3.102) . (3.103)
. (3.103) Розглянемо циліндричний конденсатор, який складається з двох коаксіальних циліндричних провідників з радіусами
Розглянемо циліндричний конденсатор, який складається з двох коаксіальних циліндричних провідників з радіусами 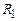 і
і  , які вставлені один в одний. Нехай між циліндрами міститься діелектрик з діелектричною проникністю
, які вставлені один в одний. Нехай між циліндрами міститься діелектрик з діелектричною проникністю 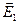 . Зовнішній циліндр тут електричного поля не створює, оскільки цей простір для нього є внутрішнім.
. Зовнішній циліндр тут електричного поля не створює, оскільки цей простір для нього є внутрішнім. , (3.104)
, (3.104) – лінійна густина заряду
– лінійна густина заряду . (3.105)
. (3.105) . (3.106)
. (3.106) . (3.107)
. (3.107) Розглянемо сферичний конденсатор, який складається з двох концентричних сферичних провідників з радіусами
Розглянемо сферичний конденсатор, який складається з двох концентричних сферичних провідників з радіусами 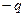 (рис. 3.21).
(рис. 3.21). рівна нулю, оскільки тут електричні поля від обох заряджених сферичних провідників взаємно компенсуються.Різницю потенціалів між обома сферичними провідниками знайдемо за формулою (3.88)
рівна нулю, оскільки тут електричні поля від обох заряджених сферичних провідників взаємно компенсуються.Різницю потенціалів між обома сферичними провідниками знайдемо за формулою (3.88)
 . 3.108)
. 3.108) . (3.109)
. (3.109) . (3.110)
. (3.110) . (3.111)
. (3.111) . (3.112)
. (3.112) Розглянемо послідовне з’єднання конденсаторів при якому негативно заряджена обкладка першого конденсатора з’єднується з позитивно зарядженою обкладкою другого, негативно заряджена обкладка другого конденсатора з’єднується з позитивно зарядженою обкладкою третього конденсатора і т.д (рис.3.23).
Розглянемо послідовне з’єднання конденсаторів при якому негативно заряджена обкладка першого конденсатора з’єднується з позитивно зарядженою обкладкою другого, негативно заряджена обкладка другого конденсатора з’єднується з позитивно зарядженою обкладкою третього конденсатора і т.д (рис.3.23). . (3.113)
. (3.113) . (3.114)
. (3.114) . (3.115)
. (3.115) . (3.156)
. (3.156) . (3.157)
. (3.157) . (3.158)
. (3.158) . (3.159)
. (3.159) . (3.160)
. (3.160)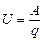 . (3.161)
. (3.161) , (3.162)
, (3.162) – електричний опір провідника.
– електричний опір провідника. . (3.163)
. (3.163) , (3.164)
, (3.164) – довжина провідника,
– довжина провідника,  – площа його поперечного перерізу,
– площа його поперечного перерізу,  – питомий опір провідника, який залежить від матеріалу з якого виготовлений провідник, і його температури. Величина обернена до питомого опору, називається питомою електропровідністю
– питомий опір провідника, який залежить від матеріалу з якого виготовлений провідник, і його температури. Величина обернена до питомого опору, називається питомою електропровідністю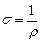 . (3.165)
. (3.165) (3.166)
(3.166) , (3.167)
, (3.167) де
де 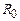 і
і  – опір і питомий опір при температурі
– опір і питомий опір при температурі  ,
,  – температурний коефіцієнт опору,
– температурний коефіцієнт опору,  – температура по шкалі Цельсія.
– температура по шкалі Цельсія. і площею поперечного перерізу
і площею поперечного перерізу  . Нехай до циліндра прикладена різниця потенціалів
. Нехай до циліндра прикладена різниця потенціалів 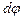 і по ньому тече струм силою
і по ньому тече струм силою  (рис. 3.27)
(рис. 3.27)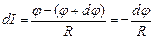 . (3.168)
. (3.168) . (3.169)
. (3.169) . (3.170)
. (3.170) . (3.171)
. (3.171)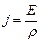 ;
;  . (3.172)
. (3.172) ;
;  . (3.173)
. (3.173)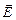 . Закон Ома в диференціальній формі зв’язує густину струму в кожній точці всередині провідника з напруженістю електричного поля в тій самій точці.
. Закон Ома в диференціальній формі зв’язує густину струму в кожній точці всередині провідника з напруженістю електричного поля в тій самій точці. напрямленого руху зарядів прямо пропорційна до напруженості поля в провіднику
напрямленого руху зарядів прямо пропорційна до напруженості поля в провіднику , (3.174)
, (3.174) називається рухливістю носіїв струму. Рухливість носіїв струму чисельно рівна швидкості їх напрямленого руху, якої вони набувають в провіднику під дією електричного поля з одиничною напруженістю.
називається рухливістю носіїв струму. Рухливість носіїв струму чисельно рівна швидкості їх напрямленого руху, якої вони набувають в провіднику під дією електричного поля з одиничною напруженістю. через поперечний переріз провідника
через поперечний переріз провідника  , (3.175)
, (3.175)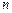 – концентрація носіїв струму,
– концентрація носіїв струму,  – заряд носія струму. Сила струму рівна
– заряд носія струму. Сила струму рівна ;
;  . (3.176)
. (3.176) . (3.177)
. (3.177) . (3.178)
. (3.178) . (3.179)
. (3.179)


