
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема1. Електростатика і постійний електричний струмСодержание книги
Поиск на нашем сайте
Тема1. ЕЛЕКТРОСТАТИКА І ПОСТІЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ Потік вектора напруженості та індукції електричного поля. Теорема Остроградського-Гауса Нехай в просторі існує електричне поле, створене деякими електричними зарядами. Розглянемо деяку поверхню з нескінченно малою площею dS (елементарну поверхню) з одиничним вектором нормалі до поверхні
де Подібним чином можна дати визначення елементарного потоку вектора індукції електричного поля, який рівний:
Потік вектора напруженості електричного поля через деяку поверхню S визначається за формулою:
Він пропорційний числу силових ліній, які пронизують цю поверхню. Потік вектора індукції електричного поля через деяку поверхню S рівний:
Розглянемо деякий точковий позитивний заряд
Підставимо (3.15) в (3.14), врахуємо, що кут між векторами
Оскільки для всіх точок сферичної поверхні величина R є постійною то, винісши постійні множники за знак інтегралу, отримаємо:
Але інтеграл по замкнутій поверхні S - це площа сферичної поверхні, яка рівна:
Підставимо вираз (3.17) в (3.16):
Український вчений М.В.Остроградський і німецький вчений К.Гаус довели, що формула (3.18) справедлива для замкненої поверхні довільної форми і довільної кількості електричних зарядів, які знаходяться всередині цієї поверхні. Тому в загальному випадку формулу (3.18) можна представити у вигляді:
Формула (3.19) – це теорема Остроградського-Гауса для напруженості електричного поля:потік вектора напруженості електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею, поділеній на діелектричну проникність середовища.
Помножимо рівняння (3.19) на
Враховуючи (3.7), отримаємо
Формула (3.21) це теорема Остроградського-Гауса для індукції електричного поля: потік вектора індукції електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею. Розглянемо випадок коли електричні заряди розподілені в просторі неперервно з деякою об’ємною густиною
Визначимо з цієї формули dq:
Проінтегрувавши вираз (3.23) по деякому об’єму V визначимо сумарний електричний заряд який міститься в цьому об’ємі:
З врахуванням формули (3.24) теорему Остроградського-Гауса (3.19) і (3.21) у випадку неперервного просторового розподілу зарядів можна представити у вигляді:
У формулах (3.25) і (3.26) інтегрування здійснюється по всьому об’єму V який обмежений замкненою поверхнею S. Тема2. Магнетизм Дія магнітного поля на струм; сила Ампера
або в скалярній формі
де α – кут між напрямками струму та магнітної індукції. Напрямок сили Ампера можна визначити за правилом лівої руки (рис. 4.12). Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (4.22) або (4.23) інтегруванням по всій довжині провідника:
Зокрема, для прямолінійного провідника довжиною
Магнітне поле в речовині Всі речовини складаються з атомів, в яких по замкнених траєкторіях рухаються електрони. Орбітальний рух електрона можна розглядати як коловий струм (мікрострум) з магнітним моментом
В залежності від наявності чи відсутності (рівності нулю) магнітного моменту, всі атоми поділяються на діамагнітні, для яких Будь-яка речовина, як система атомів, в зовнішньому магнітному полі намагнічується, тобто набуває магнітного моменту. Для кількісного опису цього явища вводять вектор намагніченості Встановлено, що вектор намагніченості пропорційний до вектора напруженості намагнічуючого поля: де безрозмірний коефіцієнт пропорційності c називається магнітною сприйнятливістю речовини. Таким чином, магнітне поле в речовині складається з зовнішнього (намагнічуючого) поля
Безрозмірна величина
Парамагнетиками є речовини, атоми або молекули яких у відсутності зовнішнього поля мають відмінний від нуля магнітний момент І діа- і парамагнетики належать до слабомагнітних речовин, оскільки для обох
Крім великої магнітної проникливості 1) на відміну від парамагнетиків, феромагнетики намагнічуються до насичення вже в слабких полях; 2) магнітна проникливість феромагнетика залежить від напруженості намагнічуючого поля (рис. 4.21): спочатку швидко зростає із збільшенням Н, досягає максимуму, а потім спадає, прямуючи до одиниці в сильних полях. 3) залежність B(H) (рис. 4.22) має гістерезисний характер. При розміщенні розмагніченого феромагнетика в зовнішньому полі залежність В(Н) описується спочатку кривою 0-1. При зменшенні Н до нуля В(Н) змінюється по кривій 1-2; тобто має місце відставання зміни індукції від зміни напруженості. Це явище називається магнітним гістерезисом. Магнітна індукція, що зберігається у феромагнетику після зникнення зовнішнього поля (при Н = 0), називається залишковою магнітною індукцією Властивості феромагнетиків пояснюються наявністю в них областей, які у відсутності зовнішнього поля спонтанно намагнічені до насичення; ці області називаються доменами. Розміри доменів ~ (
Закон Кулона: сила взаємодії двох точкових нерухомих електричних зарядів прямо пропорційна добуткові цих зарядів, обернено пропорційна квадратові відстані між ними і напрямлена вздовж прямої, яка сполучає ці заряди: Силовою лінією електричного поля називається така лінія, в кожній точці якої вектор напруженості є дотичним до самої лінії.
Електричною індукцією (електричним зміщенням) називається векторна фізична величина, яка пропорційна до напруженості, не залежить від діелектричних властивостей середовища і визначається рівністю:
Теорема Остроградського-Гауса для напруженості електричного поля:потік вектора напруженості електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею, поділеній на діелектричну проникність середовища: Теорема Остроградського-Гауса для індукції електричного поля: потік вектора індукції електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею. Теорема про циркуляцію вектора напруженості електричного поля: циркуляція вектора напруженості електростатичного поля по замкнутому контуру рівна нулю.
Еквіпотенціальна поверхня - це поверхня однакового потенціалу. Електричним диполем називається система двох однакових за модулем різнойменних зарядів. Плечемдиполя називається вектор Дипольним моментом називається векторна фізична величина, рівна добутку позитивного заряду на плече диполя: Провідниками називаються тіла, які мають вільні електричні заряди, тобто такі заряджені частинки, які можуть вільно переміщатись по об’єму провідника. Електроємністю відокремленого провідника називається фізична величина рівна зарядові, який необхідно надати провідникові, щоб змінити його потенціал на одиницю. Електроємністю конденсатора називається фізична величина, рівна зарядові, який необхідно перенести з однієї обкладки на іншу, щоб різниця потенціалів між ними змінилась на одиницю: Електричним струмом називається впорядковане переміщення електричних зарядів. Силою струму називається скалярна фізична величина, рівна зарядові, який проходить через поперечний переріз провідника за одиницю часу Закон Ома для однорідної ділянки кола: сила струму в провіднику прямо пропорційна прикладеній напрузі і обернено пропорційна опору провідника. Електрорушійною силою називається фізична величина, рівна роботі сторонніх сил по переміщенню одиничного позитивного заряду по замкнутому електричному колу. Закон Джоуля-Ленца в інтегральній формі: кількість теплоти, яка виділяється в провіднику при проходженні електричного струму, прямо пропорційна квадрату сили струму, опору провідника і часу проходження струму. Закон Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомому опору провідника і квадратові густини струму.
Магнітне поле – це особливий вид матерії, що створюється рухомими електричними зарядами (струмами) і діє на рухомі заряди, провідники зі струмом та постійні магніти. Закону Біо-Савара-Лапласа: Циркуляцією вектора Сила Ампера Сила Лоренца Теорема Гауса для магнітного поля: магнітний потік через будь-яку замкнену поверхню дорівнює нулю: магнітний потік через площину контура пропорційний до сили струму в контурі: називається індуктивністю контура Згідно з законом Фарадея зміна магнітного потоку викликає появу е.р.с. індукції, яка в даному випадку називається е.р.с. самоіндукції. Властивості феромагнетиків пояснюються наявністю в них областей, які у відсутності зовнішнього поля спонтанно намагнічені до насичення; ці області називаються доменами.
Тема1. ЕЛЕКТРОСТАТИКА І ПОСТІЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.79.178 (0.009 с.) |

 , як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна
, як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна 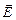 .
. Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:
Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні: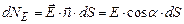 , (3.10)
, (3.10) – кут між векторами
– кут між векторами 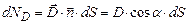 . (3.11)
. (3.11) . (3.12)
. (3.12) . (3.13)
. (3.13)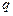 , який помістимо в центрі сферичної поверхні S радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню
, який помістимо в центрі сферичної поверхні S радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню . (3.14)
. (3.14) Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна
Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна . (3.15)
. (3.15) .
. .
.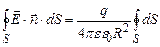 . (3.16)
. (3.16) . (3.17)
. (3.17) . (3.18)
. (3.18) . (3.19)
. (3.19) . Враховуючи, що цей множник постійний, внесемо його під знак інтегралу:
. Враховуючи, що цей множник постійний, внесемо його під знак інтегралу: . (3.20)
. (3.20) . (3.21)
. (3.21) . Об’ємною густиною електричного зарядуназивається фізична величина, рівна електричному зарядові в одиниці об’єму простору:
. Об’ємною густиною електричного зарядуназивається фізична величина, рівна електричному зарядові в одиниці об’єму простору: . (3.22)
. (3.22) . (3.23)
. (3.23) . (3.24)
. (3.24) . (3.25)
. (3.25) . (3.26)
. (3.26) Як відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом
Як відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом 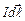 , вміщений в магнітне поле індукцією
, вміщений в магнітне поле індукцією  , діє сила (сила Ампера)
, діє сила (сила Ампера) (4.22)
(4.22) , (4.23)
, (4.23) (4.24)
(4.24)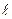 в однорідному магнітному полі
в однорідному магнітному полі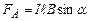 . (4.25)
. (4.25)
 – частота обертання електрона, r – радіус орбіти,
– частота обертання електрона, r – радіус орбіти, 
 і парамагнітні, для яких
і парамагнітні, для яких  .
. – фізичну величину, що дорівнює магнітному моменту одиниці об’єму магнетика:
– фізичну величину, що дорівнює магнітному моменту одиниці об’єму магнетика:  . (4.50)
. (4.50) , (4.51)
, (4.51) , створеного макрострумами, і власного поля
, створеного макрострумами, і власного поля  , створеного мікрострумами. В діамагнітних речовинах власне поле напрямлене проти зовнішнього, а в парамагнітних – напрямки зовнішнього і власного полів співпадають. За принципом суперпозиції магнітна індукція поля в речовині
, створеного мікрострумами. В діамагнітних речовинах власне поле напрямлене проти зовнішнього, а в парамагнітних – напрямки зовнішнього і власного полів співпадають. За принципом суперпозиції магнітна індукція поля в речовині
 називається магнітною проникністю речовини. Тоді остаточно запишемо
називається магнітною проникністю речовини. Тоді остаточно запишемо
 (4.52)
(4.52)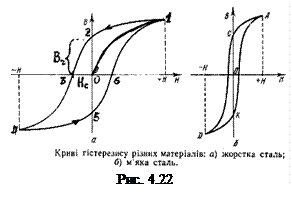 Тепер дамо елементарне пояснення природи діа- і парамагнетизму. У діамагнетиків сумарний магнітний момент атомів у відсутності зовнішнього поля дорівнює нулю. Досліди показують, що магнітного моменту не має атом гелію. Цей факт можна пояснити, припустивши, що два електрони атома гелію обертаються навколо ядра по орбітах рівних радіусів, з рівними за величиною швидкостями, але в протилежних напрямках. Тому їхні магнітні моменти взаємно скомпенсовані і результуючий магнітний момент атома дорівнює нулю. Зовнішнє магнітне поле, впливаючи на рух електронів атома, індукує в ньому магнітний момент, який за правилом Ленца (див. §4.8.) напрямлений проти
Тепер дамо елементарне пояснення природи діа- і парамагнетизму. У діамагнетиків сумарний магнітний момент атомів у відсутності зовнішнього поля дорівнює нулю. Досліди показують, що магнітного моменту не має атом гелію. Цей факт можна пояснити, припустивши, що два електрони атома гелію обертаються навколо ядра по орбітах рівних радіусів, з рівними за величиною швидкостями, але в протилежних напрямках. Тому їхні магнітні моменти взаємно скомпенсовані і результуючий магнітний момент атома дорівнює нулю. Зовнішнє магнітне поле, впливаючи на рух електронів атома, індукує в ньому магнітний момент, який за правилом Ленца (див. §4.8.) напрямлений проти  .
. ; наприклад, якщо вони мають непарне число електронів в атомі. Тепловий рух робить орієнтацію магнітних моментів атомів хаотичною, тому у відсутності зовнішнього поля парамагнетик не намагнічений
; наприклад, якщо вони мають непарне число електронів в атомі. Тепловий рух робить орієнтацію магнітних моментів атомів хаотичною, тому у відсутності зовнішнього поля парамагнетик не намагнічений  . В зовнішньому полі магнітні моменти атомів орієнтуються вздовж поля (див.§4.1.), тому парамагнетик намагнічується в напрямку зовнішнього поля. Для парамагнетиків
. В зовнішньому полі магнітні моменти атомів орієнтуються вздовж поля (див.§4.1.), тому парамагнетик намагнічується в напрямку зовнішнього поля. Для парамагнетиків 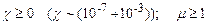 . Магнітна сприйнятливість парамагнетика в слабких полях і при досить високих температурах обернено пропорційна до температури (закон Кюрі):
. Магнітна сприйнятливість парамагнетика в слабких полях і при досить високих температурах обернено пропорційна до температури (закон Кюрі):  , де С – стала Кюрі, що залежить від роду парамагнетика.
, де С – стала Кюрі, що залежить від роду парамагнетика.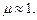 Але існують сильномагнітні речовини – феромагнетики, у яких магнітна проникливість досягає
Але існують сильномагнітні речовини – феромагнетики, у яких магнітна проникливість досягає  . Крім основного представника – заліза, до феромагнетиків належать Co, Ni, ряд рідкісноземельних елементів та сплавів на їх основі. Відома наступна властивість феромагнетиків: при температурі, що називається точкою Кюрі (залежить від речовини), феромагнетик стрибком втрачає свої феромагнітні властивості і переходить у парамагнітний стан. Це означає, що атом феромагнетика подібний до атома парамагнетика відмінністю від нуля магнітного моменту, а феромагнітні властивості притаманні не окремому атому, а кристалу феромагнітної речовини в цілому при температурах, нижчих від точки Кюрі.
. Крім основного представника – заліза, до феромагнетиків належать Co, Ni, ряд рідкісноземельних елементів та сплавів на їх основі. Відома наступна властивість феромагнетиків: при температурі, що називається точкою Кюрі (залежить від речовини), феромагнетик стрибком втрачає свої феромагнітні властивості і переходить у парамагнітний стан. Це означає, що атом феромагнетика подібний до атома парамагнетика відмінністю від нуля магнітного моменту, а феромагнітні властивості притаманні не окремому атому, а кристалу феромагнітної речовини в цілому при температурах, нижчих від точки Кюрі. феромагнетики відрізняються від слабомагнітних речовин рядом властивостей:
феромагнетики відрізняються від слабомагнітних речовин рядом властивостей: (постійні магніти). Щоб розмагнітити феромагнетик, потрібно прикласти зовнішнє поле протилежного напрямку з напруженістю
(постійні магніти). Щоб розмагнітити феромагнетик, потрібно прикласти зовнішнє поле протилежного напрямку з напруженістю  , яка називається коерцитивною силою. При подальшому збільшенні напруженості відбувається намагнічування протилежного напрямку по кривій 3-4. Ділянка 4-5-6 знову відповідає розмагнічуванню. Надалі процес перемагнічування відбувається по замкненій кривій 6-1-2-3-4-5-6 (рис. 4.22), яка називається петлею гістерезису. В залежності від величини Нс усі феромагнітні матеріали поділяють на жорсткі (рис.4.22, а) і м’які (рис.4.22, б).
, яка називається коерцитивною силою. При подальшому збільшенні напруженості відбувається намагнічування протилежного напрямку по кривій 3-4. Ділянка 4-5-6 знову відповідає розмагнічуванню. Надалі процес перемагнічування відбувається по замкненій кривій 6-1-2-3-4-5-6 (рис. 4.22), яка називається петлею гістерезису. В залежності від величини Нс усі феромагнітні матеріали поділяють на жорсткі (рис.4.22, а) і м’які (рис.4.22, б). ) м. Розташування і намагніченість доменів такі, що у відсутності зовнішнього поля сумарна намагніченість дорівнює нулю. В зовнішньому полі вектори намагніченості доменів частково повертаються в напрямку поля і феромагнетик намагнічується.
) м. Розташування і намагніченість доменів такі, що у відсутності зовнішнього поля сумарна намагніченість дорівнює нулю. В зовнішньому полі вектори намагніченості доменів частково повертаються в напрямку поля і феромагнетик намагнічується.

 .
. Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:
Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:  Потенціалом електричного поля називається скалярна фізична величина рівна потенціальній енергії одиничного позитивного точкового заряду вміщеного в дану точку поля:
Потенціалом електричного поля називається скалярна фізична величина рівна потенціальній енергії одиничного позитивного точкового заряду вміщеного в дану точку поля:  .
. напрямлений від негативного заряду до позитивного.
напрямлений від негативного заряду до позитивного. .
.


 по замкненому контуру називається інтеграл
по замкненому контуру називається інтеграл  де
де  - вектор елементу довжини контура, напрямлений вздовж обходу контура,
- вектор елементу довжини контура, напрямлений вздовж обходу контура,  – проекція
– проекція  ,
,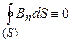 .(4.36)
.(4.36) або
або  ,де L – коефіцієнт пропорційності між силою струму в контурі і магнітним потоком, що перетинає цей контур, який
,де L – коефіцієнт пропорційності між силою струму в контурі і магнітним потоком, що перетинає цей контур, який



