
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок електричних полів за допомогою теореми Остроградського-ГаусаСодержание книги
Поиск на нашем сайте
Для розрахунку електричного поля створеного зарядженим тілом необхідно розбити це тіло на точкові заряди і визначити напруженість електричного поля в деякій точці простору за принципом суперпозиції. Для багатьох тіл такі розрахунки математично досить складні. Для деяких симетричних тіл розрахунок електричного поля значно спрощується при використанні теореми Остроградського-Гауса. Розглянемо деякі приклади таких розрахунків. а) Електричне поле рівномірно зарядженої кулі. Розглянемо кулю радіусом R рівномірно заряджену по об’єму з об’ємною густиною заряду
Для рівномірного розподілу заряду можна вважати що
Оскільки об’єм кулі рівний
то підставивши (3.29) в (3.28) одержимо:
Виберемо замкнену поверхню S у формі сфери радіусом r, центр якої співпадає з центром зарядженої кулі, як зображено на рис. 3.5. Розглянемо випадок коли
або
В даному випадку
Виходячи з міркувань симетрії випливає, що величина Е за модулем постійна у всіх точках сферичної поверхні S, тому винесемо Е за знак інтегралу:
У формулі (3.34) інтеграл по замкненій поверхні рівний площі сферичної поверхні радіусом r а інтеграл по об’єму V рівний об’єму цієї ж сферичної поверхні, тому
Підставимо вирази (3.30), (3.35) і (3.36) у формулу (3.34):
Розглянемо випадок коли
або
Оскільки вектори
Підставимо (3.35) в (3.40):
Із формули (3.41) випливає, що ззовні зарядженої кулі напруженість електричного поля, так само як і для точкового заряду, обернено пропорційна квадратові відстані від центру кулі до даної точки простору. На рис. 3.7 зображено залежність напруженості електричного поля Е від відстані r. б) Електричне поле нескінченої рівномірно зарядженої прямої. Розглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду
Лінійною густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці довжини лінії вздовж якої він розподілений. У випадку рівномірного розподілу електричного заряду
де В якості замкненої поверхні виберемо циліндричну поверхню радіусом r, висотою
Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів: по бічній поверхні, по першій і другій основах. Сумарний заряд, який охоплений поверхнею S, рівний зарядові на ділянці прямої довжиною
Підставимо (3.45) в (3.44):
Оскільки
З міркувань симетрії випливає, що модуль Е є однаковим в усіх точках бічної поверхні. Тому винесемо Е за знак інтегралу:
Інтеграл по бічній поверхні рівний площі цієї поверхні:
Підставимо (3.47) у (3.46):
З цієї формули випливає, що напруженість електричного поля, створеного нескінченою рівномірно зарядженою прямою обернено пропорційна до відстані між даною точкою простору і прямою. Ця формула справедлива також для нескінченого прямого рівномірно зарядженого циліндра. в) Електричне поле нескінченної рівномірно зарядженої площини. Розглянемо нескінченну площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду
Поверхневою густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці площі поверхні по якій розподілений заряд. У випадку рівномірного розподілу електричного заряду q по поверхні S поверхнева густина заряду рівна:
В якості замкненої поверхні виберемо циліндричну поверхню з площею основи Застосуємо теорему Остроградського-Гауса
Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів. Сумарний заряд, який охоплений поверхнею S рівний зарядові круга площею Sосн ., який вирізує циліндр S на зарядженій площині. Виходячи із формули (3.50), цей заряд рівний
Підставимо (3.52) в (3.51):
Оскільки
Інтеграли по поверхнях основ рівні:
Підставимо (3.54) в (3.53):
Із формули (3.55) випливає, що напруженість електричного поля, створеного нескінченною рівномірно зарядженою площиною не залежить від відстані до площини, тобто є однаковою в усіх точках простору по обидва боки від зарядженої площини. Це електричне поле є однорідним. Його силові лінії перпендикулярні до зарядженої площини.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.006 с.) |

 . (3.27)
. (3.27)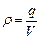 . (3.28)
. (3.28)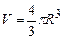 , (3.29)
, (3.29)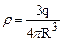 . (3.30)
. (3.30)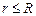 , тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.
, тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.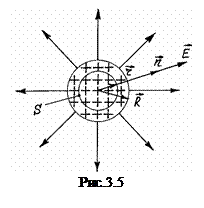
 (3.31)
(3.31)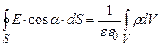 (3.32)
(3.32)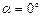 і
і 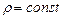 , тому
, тому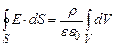 . (3.33)
. (3.33)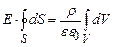 . (3.34)
. (3.34)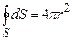 , (3.35)
, (3.35)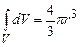 . (3.36)
. (3.36)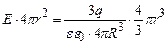
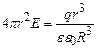
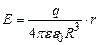 . (3.37)
. (3.37)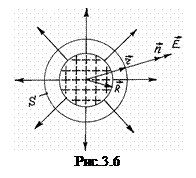 Отже всередині рівномірно зарядженої по об’єму кулі напруженість електричного поля прямо пропорційна відстані від центру кулі до даної точки.
Отже всередині рівномірно зарядженої по об’єму кулі напруженість електричного поля прямо пропорційна відстані від центру кулі до даної точки.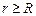 , тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.
, тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.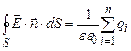 (3.38)
(3.38)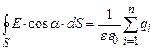 . (3.39)
. (3.39)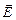 і
і 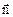 мають однаковий напрямок то
мають однаковий напрямок то 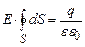 . (3.40)
. (3.40)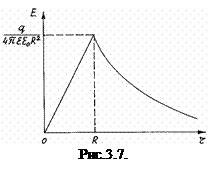
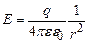 . (3.41)
. (3.41)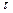 .
.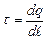 . (3.42)
. (3.42) , (3.43)
, (3.43)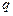 – електричний заряд який розподілений вздовж лінії довжиною
– електричний заряд який розподілений вздовж лінії довжиною  .
. , вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса:
, вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса: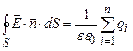 . (3.44)
. (3.44)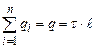 . (3.45)
. (3.45)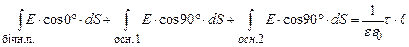
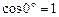 і
і 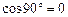 , то одержимо:
, то одержимо: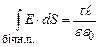 .
.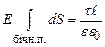 . (3.46)
. (3.46)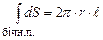 . (3.47)
. (3.47)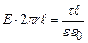
 . (3.48)
. (3.48)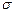 :
: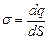 . (3.49)
. (3.49)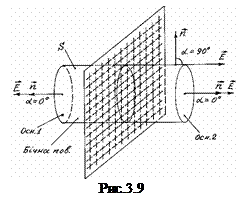
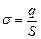 . (3.50)
. (3.50)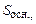 вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.
вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.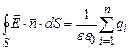 . (3.51)
. (3.51)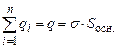 (3.52)
(3.52)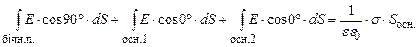
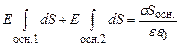 . (3.53)
. (3.53)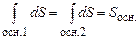 (3.54)
(3.54)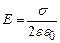 . (3.55)
. (3.55)


