
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регулировочные свойства электрических машинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РЕГУЛИРОВОЧНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ МАШИН Физическое обоснование регулировочных свойств коллекторных двигателей постоянного тока В классической теории машин постоянного тока формулу для электромагнитного момента получают, исходя из выражения для силы, действующей на проводник с током, находящимся в магнитном поле. Поскольку якорные обмотки состоят из витков, определим момент, который действует на плоский контур с током
Рис. 1.3 На рисунке 1.3,а) приняты следующие обозначения: Электромагнитные силы стремятся расположить жесткие контуры системы таким образом, чтобы каждый контур охватывал возможно большую часть внешнего потока при условии, что токи в контурах постоянны.
Искомый вращающий момент можно представить как произведение тока
Произведение
Таким образом, вращающий момент не зависит отдельно от Расположим виток, образованный двумя прямолинейными проводниками, в магнитном поле, как показано на рисунке 1.3, б). Ось магнитного поля Применяя соотношение (1.4), дадим физическое обоснование резкому отличительному свойству МПТ и синхронных машин, проявляющееся при регулировании тока возбуждения. Рассмотрим на примере двигательного режима, когда
В СМ, чтобы соблюдалось условие
одновременно изменяются ток якоря и угол Поскольку в МПТ угол
Нарушение баланса мощностей приводит к появлению динамического момента, под
Становится физически наглядным так называемый «разнос» двигателя, когда при обрыве цепи возбуждения магнитный поток уменьшается до величины остаточного магнитного потока, и в соответствии с (1.4) ток якоря может достичь недопустимо большой величины. Изменение скорости якоря приводит к изменению частоты индуктируемой ЭДС, что позволяет рассматривать коллектор с щетками как преобразователь частоты. Такой подход к обоснованию регулировочных свойств применим как к вентильным двигателям с замкнутой многосекционной обмоткой якоря, так и к вентильным двигателям, выполненных на базе синхронных машин. При всех способах регулирования скорости система управления инвертором должна обеспечить постоянство угла между осями полей возбуждения и якоря. Как следует из вышеизложенного, если этот угол поддерживать близким к значению, равным
ЭЛЕКТРИЧЕСКИЕ МАШИНЫ ПОСТОЯННОГО ТОКА С ПОЛУПРОВОДНИКОВЫМИ КОММУТАТОРАМИ Учет процесса коммутации В реальных случаях индуктивное сопротивление при переключении вентилей не равно нулю. Поэтому время, за которое ток в отключаемом вентиле спадает от
или
где LK и Сопротивление коммутации
где
Поэтому окончательно получаем:
Поскольку обычно
В оценочных расчетах часто принимают значение Хк равным индуктивному сопротивлению рассеяния якорной обмотки Так как во время коммутации
Поэтому согласно (2.3) будет:
Обозначим через
После подстановки (2.6) в формулу (2.5) получим:
Путем интегрирования (2.7), учитывая, что при
Поскольку при
Из этого выражения можно определить длительность коммутации
Отсюда можно сделать вывод, что сростом Уравнение (2.8) можно записать для номинального режима в безразмерном виде, если поделить обе его части на
Здесь
Рис. 2.5 существенна. На этом основании при инженерных расчетах часто аппроксимируют кривую Напряжение на коммутирующих вентилях ит равно полусумме напряжений отключающейся и включающейся фазы. Действительно, согласно (2.3):
Складывая оба выражения и деля результат на 2 получим:
Таким образом, во время коммутации напряжение снижается по сравнению с напряжением включающейся фазы, которое действовало бы без коммутации. Коммутация возникает с периодичностью
откуда с учетом условия
Окончательно, с учетом (2.2) среднее значение выпрямленного напряжения равно: РЕГУЛИРОВОЧНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ МАШИН
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.140.88 (0.009 с.) |

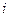 во внешнем магнитном поле.
во внешнем магнитном поле.
 - магнитная индукция внешнего поля;
- магнитная индукция внешнего поля;  - угол, составленный положительной нормалью
- угол, составленный положительной нормалью  к этой поверхности с вектором
к этой поверхности с вектором  .
. .
.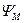 по углу
по углу 
 ,
, . (1.4)
. (1.4) называют магнитным моментом замкнутого тока. В векторной форме выражение (1.4) имеет вид:
называют магнитным моментом замкнутого тока. В векторной форме выражение (1.4) имеет вид: .
. .
. , созданного током
, созданного током  между взаимодействующими магнитными полями возбуждения и якоря в ЭМ эквивалентен углу
между взаимодействующими магнитными полями возбуждения и якоря в ЭМ эквивалентен углу  .
. ,
, между осями полей возбуждения и якоря, и ротор продолжает вращаться синхронно. При этом изменяется лишь реактивная составляющая тока, а активная составляющая тока и активная мощность остаются постоянными. Отличительной особенностью МПТ от СМ является то обстоятельство, что при щетках, установленных по линии геометрической нейтрали, поток реакции якоря независимо от нагрузки направлен по поперечной оси. Поэтому угол между осями полей возбуждения и якоря остается постоянным и равным
между осями полей возбуждения и якоря, и ротор продолжает вращаться синхронно. При этом изменяется лишь реактивная составляющая тока, а активная составляющая тока и активная мощность остаются постоянными. Отличительной особенностью МПТ от СМ является то обстоятельство, что при щетках, установленных по линии геометрической нейтрали, поток реакции якоря независимо от нагрузки направлен по поперечной оси. Поэтому угол между осями полей возбуждения и якоря остается постоянным и равным  .
. , то изменение тока возбуждения вызывает в соответствии с выражением (1.4) изменение тока якоря в обратном направлении. Но поскольку во внешней цепи протекает постоянный ток, то изменение тока якоря приводит к изменению активной мощности:
, то изменение тока возбуждения вызывает в соответствии с выражением (1.4) изменение тока якоря в обратном направлении. Но поскольку во внешней цепи протекает постоянный ток, то изменение тока якоря приводит к изменению активной мощности: .
. , определяемой из равенства, если не учитывать потери:
, определяемой из равенства, если не учитывать потери:
 , то от двигателя можно получить максимальную мощность.
, то от двигателя можно получить максимальную мощность. до 0, а во включаемом вентиле нарастает от 0 до
до 0, а во включаемом вентиле нарастает от 0 до  (рис. 2.4, б ). При одновременной работе вентилей 1 и 2(рис. 2.3)ветви с обмотками фазА и Ввключены параллельно и напряжение на их концах одинаковое. Поэтому, если пренебречь активными сопротивлениями обмоток и вентилей, имеем:
(рис. 2.4, б ). При одновременной работе вентилей 1 и 2(рис. 2.3)ветви с обмотками фазА и Ввключены параллельно и напряжение на их концах одинаковое. Поэтому, если пренебречь активными сопротивлениями обмоток и вентилей, имеем:
 (2.3)
(2.3) — индуктивность и индуктивное сопротивление обмотки фазы во время коммутации.
— индуктивность и индуктивное сопротивление обмотки фазы во время коммутации. соответствует ЭДС самоиндукции, наводимой в обмотках быстро изменяющимися магнитными потоками во время коммутации. Поскольку это время мало, потоки, соответствующие ХК,замыкаются примерно по тем же путям, что и потоки при внезапном коротком замыкании генератора. Поэтому параметр Хк имеет порядок
соответствует ЭДС самоиндукции, наводимой в обмотках быстро изменяющимися магнитными потоками во время коммутации. Поскольку это время мало, потоки, соответствующие ХК,замыкаются примерно по тем же путям, что и потоки при внезапном коротком замыкании генератора. Поэтому параметр Хк имеет порядок  .Более точный анализ показывает, что процесс коммутации вентилей близок по своей физической природе к начальной стадии внезапного двухфазнoro короткого замыкания генератора и поэтому
.Более точный анализ показывает, что процесс коммутации вентилей близок по своей физической природе к начальной стадии внезапного двухфазнoro короткого замыкания генератора и поэтому , (2.4)
, (2.4) — индуктивное сопротивление обратного следования фаз, приближенно выражаемое в виде:
— индуктивное сопротивление обратного следования фаз, приближенно выражаемое в виде: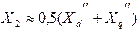
 .
. не сильно отличается от
не сильно отличается от  ,в более грубомприближении будет:
,в более грубомприближении будет:
 .
. = const, то
= const, то .
.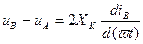 . (2.5)
. (2.5) . В общем случае:
. В общем случае: . (2.6)
. (2.6) (2.7)
(2.7) ток
ток  , найдем:
, найдем: . (2.8)
. (2.8) период коммутации завершается и
период коммутации завершается и  , из равенства (2.8) имеем:
, из равенства (2.8) имеем: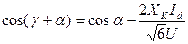 . (2.9)
. (2.9) , получим:
, получим: .
. , где
, где  - коэффициент преобразования тока.
- коэффициент преобразования тока.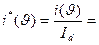

 . (2.10)
. (2.10) - относительное индуктивное коммутационное сопротивление.
- относительное индуктивное коммутационное сопротивление. На рис. 2.5 приведены кривые
На рис. 2.5 приведены кривые  для
для  = 0,1 (сплошные линии) и
= 0,1 (сплошные линии) и  10... 15° зависимости
10... 15° зависимости  .
. ,
, .
.
 , поэтому из-за коммутации среднее значение падения выпрямленного напряжения равно:
, поэтому из-за коммутации среднее значение падения выпрямленного напряжения равно: ,
, . (2.11)
. (2.11)


